This notebook contains course material from CBE20255 by Jeffrey Kantor (jeff at nd.edu); the content is available on Github. The text is released under the CC-BY-NC-ND-4.0 license, and code is released under the MIT license.
Energy Balances for a Steam Turbine¶
Summary¶
The notebook presents shows how to set up and solve the energy balances for a steam turbine flowsheet. The example demonstrates the use of steam tables.
Problem Statement¶
10 kg/sec of water at 1 bar absolute pressure and 50 $^\circ$C is pumped isothermally to a pressure of 10 bar absolute, then fed to a boiler. The net heat input to the boiler is 29,490 kJ/sec. The boiler produces steam at 10 bar absolute which then enters a turbine. The exhaust leaving the turbine is saturated steam at 1 bar absolute.
- What is the pump work?
- What is the temperature of the steam produced by the boiler?
- What is the turbine work produced?
- What is the thermal efficiency (i.e., net work out/net heat in) for this system?
- Locate the outlet conditions of the boiler and of the steam turbine on the attached T-S diagram. Do the specifications satisfy the second law of thermodynamics?
Steam tables are provided. If needed, you can assume the heat capacity of liquid water is 4.2 kJ/kg-C and for steam is 1.9 kJ/kg-C.
Solution¶
The first step in the analysis is to draw a flowsheet showing what is known and what is unknown.
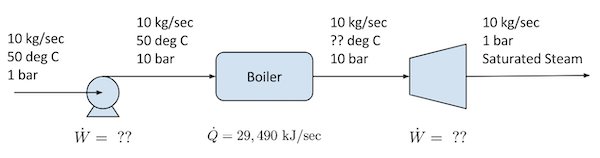
The problem requires an energy balance for each process unit. The generic energy balance reads
$$\frac{dE_{sys}}{dt} = \dot{m}_{in}\hat{H}_{in} - \dot{m}_{out}\hat{H}_{out} + \dot{W} + \dot{Q}$$where each term denotes a rate at which energy is transferred or work is done with units of power. At steady state the rate of change of system energy is zero, and mass inflow equal to outflow, $\dot{m}_{in} = \dot{m}_{out}$. The energy balance for each unit can be written as
$$0 = \dot{m}(\hat{H}_{in} - \hat{H}_{out})+ \dot{W} + \dot{Q}$$This energy balance will be applied to each of three units in the flowsheet.
Part a. What is the pump work?¶
The pump is operated by a motor which provides work but no substantial amount of heat. The energy balance reduces to
$$0 = \dot{m}(\hat{H}_{in} - \hat{H}_{out}) + \dot{W}_{pump}$$then solving for the pump work
$$\dot{W}_{pump} = \dot{m}(\hat{H}_{in} - \hat{H}_{out})$$Substituting for enthalpy $\hat{H} = \hat{U} + P\hat{V}$,
$$\dot{W}_{pump} = \dot{m}([\hat{U}_{out} + P_{out}\hat{V}_{out}] - [\hat{U}_{in} + P_{in}\hat{V}_{in}])$$Rearranging,
$$\dot{W}_{pump} = \dot{m} (\hat{U}_{out} - \hat{U}_{in} + P_{out}\hat{V}_{out} - P_{in}\hat{V}_{in})$$The internal energy of liquid water is, to a good approximation, a function of temperature alone, so $\hat{U}_{out} \approx \hat{U}_{in}$. Liquid water is also very nearly incompressible which implies the specific volume is constant $\hat{V}_{out} \approx \hat{V}_{in}$. So to a good approximation
$$\dot{W}_{pump} \approx \dot{m}V(Pout - Pin)$$The specific volume of water is 0.001 m$^3$ per kg. Expressing pressure in Pascals gives a straightforward calculation
\begin{align*} \dot{W}_{pump} & = 10\frac{kg}{sec} \times 0.001 \frac{m^3}{kg}(10.0\times 10^5 \frac{N}{m^2} - 1.0\times 10^5\frac{N}{m^2}) \\ & = 9,000 N-m/sec \\ & = 9 kilowatts \end{align*}At 746 watts per horsepower this corresponds to a work requirement of about 12 hp. In practice, a larger motor would be required to accommodate pump inefficiencies and other operational factors.
Part b. What is the temperature of the steam produced by the boiler?¶
The boiler has a large input of thermal energy, and the amount of mechanical work is negligible. The energy balance is then
$$\dot{Q}_{pump} = \dot{m}(\hat{H}_{out} - \hat{H}_{in})$$The water flowing through the boiler begins at 50 $^\circ$C and 10 bar, is heated to saturation temperature which point it vaporizes, and the resulting steam heated to the exit temperature. The change in specific enthalpy is given as the sum of these three processes
$$\hat{H}_{out} - \hat{H}_{in} = \Delta\hat{H}_{50^\circ C\rightarrow T_{sat}} + \Delta\hat{H}_v + \Delta\hat{H}_{T_{sat} \rightarrow T_{exit}}$$The steam table provides the essential information on saturation temperature and enthalpy of vaporization at 10 bar.
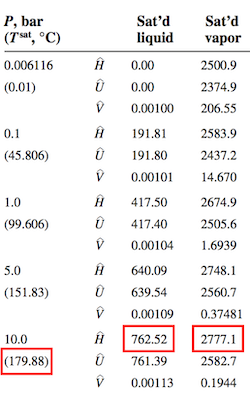
Calculating each of the three terms
\begin{align*} \Delta\hat{H}_{50^\circ C\rightarrow T_{sat}} & = C_{p,liq}(T_{sat}-50) \\ & = 4.2 \frac{kJ}{kg ^\circ C} (179.88^\circ C-50^\circ C) \\ & = 545.5 \frac{kJ}{kg} \\ \\ \Delta\hat{H}_v & = 2777.1 \frac{kJ}{kg} - 762.52 \frac{kJ}{kg} = 2,014.6 \frac{kJ}{kg} \\ \\ \Delta\hat{H}_{T_{sat} \rightarrow T_{exit}} & = 1.9 \frac{kJ}{kg ^\circ C}(T_{exit}-179.88^\circ C) \end{align*}Rearranging the energy balance
$$\hat{H}_{out} - \hat{H}_{in} = \frac{\dot{Q}}{\dot{m}}$$Substituting for $\hat{H}_{out} - \hat{H}_{in}$
$$545.5\frac{kJ}{kg} + 2,014.6 \frac{kJ}{kg} + 1.9 \frac{kJ}{kg\circ C}(T_{exit} - 179.88^\circ C) = \frac{29,490 \frac{kJ}{sec}}{10\frac{kg}{sec}}$$Solving for the unknown exit temperature
\begin{align*} T_{exit} & = 179.88^\circ C + \frac{\frac{29,490 \frac{kJ}{sec}}{10\frac{kg}{sec}} - 545.5 \frac{kJ}{kg} -2,014.6 \frac{kJ}{kg}}{1.9 \frac{kJ}{kg^\circ C}} \\ & = 179.88^\circ C + 204.7^\circ C \\ & = 385$^\circ$C \end{align*}Part c. How much turbine work is produced?¶
Because the turbine exchanges very little thermal energy with the surroundings, energy balance for the turbine is
$$0 = \dot{m}(\hat{H}_{out} - \hat{H}_{in}) - \dot{W}_{turbine}$$Note that the sign of $\dot{W}_{turbine}$ has been changed to correspond to the production of work by the turbine rather the usual convention where work is done on the system. Solving for $\dot{W}_{turbine}$
$$\dot{W}_{turbine} = \dot{m}(\hat{H}_{out} - \hat{H}_{in})$$The turbine outlet consists of saturated water vapor at 1 bar. From the steam tables
$$\hat{H}_{out} = 2,674.9 \frac{kJ}{kg}$$The inlet condition is superheated vapor at 10 bar and 385$^\circ$C. The steam table does not explicitly include this condition, so the best we can do is interpolate
\begin{align*} \hat{H}_{in} & = \hat{H}(10\ bar, 350^\circ C) + 35^\circ C \times \frac{\hat{H}(10\ bar, 400^\circ C) - \hat{H}(10\ bar, 350^\circ C)}{50^\circ C} \\ & = 3,158.2 + 35\times \frac{3,264.5-3,158.2}{50} \\ & = 3,233.3 \frac{kJ}{kg} \end{align*}Calculating
\begin{align*} \dot{W}_{turbine} & = 10\frac{kg}{sec}\times(3,233.3 \frac{kJ}{kg} - 2,674.9 \frac{kJ}{kg}) \\ & = 5,584.1 \frac{kJ}{sec} \\ & = 5.58 megawatts \end{align*}Part d. What is the thermal efficiency, i.e., net work out/net heat in, for this system?¶
The thermal efficiency is given by
$$\epsilon_{thermal} = \frac{5,584.1\frac{kJ}{sec} - 9\frac{kJ}{sec}}{24.49\frac{kJ}{sec}} = 0.228 = 22.8% $$This is relatively low compared to modern power generation systems which exhibit efficiencies of 40% or higher. The main limitation in this example is the relatively modest steam temperature exiting the boiler, and the absence of steam regenerators commonly used in commercial power generation.