Application of MPBNs to the Th-differentiation model by Abou-Jaoudé et al. 2015¶
We use Most Permissive Boolean Networks to reproduce the analyses the logical model published in (Abou-Jaoudé et al., 2015) which focus on reprogramming capabilities accross different T-cell types.
import biolqm
import ginsim
import pandas as pd
from functools import reduce
This notebook has been executed using the docker image colomoto/colomoto-docker:2020-07-01
import mpbn
lrg = ginsim.load("https://zenodo.org/record/3719059/files/Frontiers-Th-Full-model-annotated.zginml?download=1")
ginsim.show(lrg)
We use biolqm to convert it to a pure Boolean model.
bn = biolqm.to_minibn(biolqm.booleanize(lrg.getModel()))
inputs = set(bn.inputs())
len(bn), len(inputs)
(103, 21)
The following code cells define the different subtypes and conditions as specified in the article.
Markers for T-cell subtypes¶
The study list various T-cell subtypes which can be identified by particular combinations of markers activities. They are specified in the Table 2 of article, reproduced herebelow:
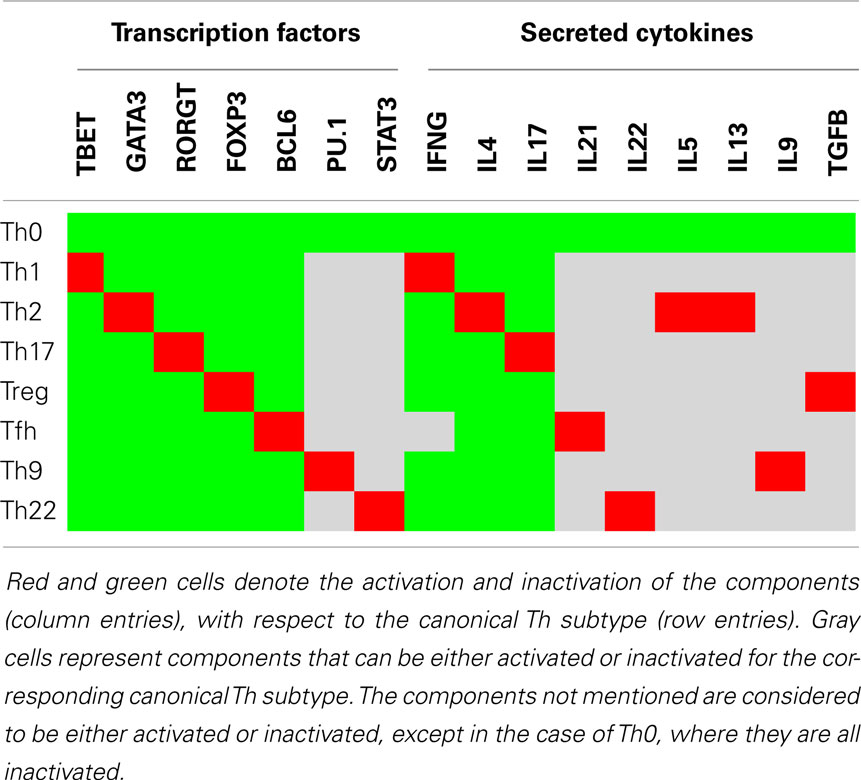
subtypes = {
"Th0": (set(),set(bn)), # all nodes are inactive
"Th1": ({"TBET", "IFNG"},
{"GATA3", "RORGT", "FOXP3", "BCL6", "IL4", "IL17"}),
"Th2": ({"GATA3", "IL4", "IL5", "IL13"},
{"TBET", "RORGT", "FOXP3", "BCL6", "IFNG", "IL17"}),
"Th17": ({"RORGT", "IL17"},
{"TBET", "GATA3", "FOXP3", "BCL6", "IFNG", "IL4"}),
"Treg": ({"FOXP3", "TGFB"},
{"TBET", "GATA3", "RORGT", "BCL6", "IFNG", "IL4", "IL17"}),
"Tfh": ({"BCL6", "IL21"},
{"TBET", "GATA3", "RORGT", "FOXP3", "IL4", "IL17"}),
"Th9": ({"PU1", "IL9"},
{"TBET", "GATA3", "RORGT", "FOXP3", "BCL6", "IFNG", "IL4", "IL17"}),
"Th22": ({"STAT3", "IL22"},
{"TBET", "GATA3", "RORGT", "FOXP3", "BCL6", "IFNG", "IL4", "IL17"}),
}
#sanity check
for t, nodes in subtypes.items():
assert nodes[0].issubset(bn) and nodes[1].issubset(bn), \
"unknown nodes for {}".format(t)
# convert to configurations
def subtype_cfg(t):
return dict([(n, 1) for n in subtypes[t][0]] \
+ [(n, 0) for n in subtypes[t][1]])
subtypes = dict([(t, subtype_cfg(t)) for t in subtypes])
types = list(subtypes.keys())
# display
tcolumns = ["TBET","GATA3","RORGT","FOXP3","BCL6","PU1","STAT3",
"IFNG","IL4","IL17","IL21","IL22","IL5","IL13","IL9","TGFB"]
assert len(tcolumns)==16,len(tcolumns)
def colordf(df):
def colorize(val):
if val == 1:
return "color: red; background-color: red"
if val == 0:
return "color: lime; background-color: lime"
if val == "*":
return "color: lightgrey; background-color: lightgrey"
return ""
return df.style.applymap(colorize)
types = list(subtypes.keys())
df = pd.DataFrame([subtypes[t] for t in types], index=types, columns=tcolumns).fillna('*')
colordf(df)
| TBET | GATA3 | RORGT | FOXP3 | BCL6 | PU1 | STAT3 | IFNG | IL4 | IL17 | IL21 | IL22 | IL5 | IL13 | IL9 | TGFB | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Th0 | 0 | 0 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Th1 | 1 | 0 | 0 | 0 | 0 | * | * | 1.000000 | 0 | 0 | * | * | * | * | * | * |
| Th2 | 0 | 1 | 0 | 0 | 0 | * | * | 0.000000 | 1 | 0 | * | * | 1.000000 | 1.000000 | * | * |
| Th17 | 0 | 0 | 1 | 0 | 0 | * | * | 0.000000 | 0 | 1 | * | * | * | * | * | * |
| Treg | 0 | 0 | 0 | 1 | 0 | * | * | 0.000000 | 0 | 0 | * | * | * | * | * | 1.000000 |
| Tfh | 0 | 0 | 0 | 0 | 1 | * | * | * | 0 | 0 | 1.000000 | * | * | * | * | * |
| Th9 | 0 | 0 | 0 | 0 | 0 | 1.000000 | * | 0.000000 | 0 | 0 | * | * | * | * | 1.000000 | * |
| Th22 | 0 | 0 | 0 | 0 | 0 | * | 1.000000 | 0.000000 | 0 | 0 | * | 1.000000 | * | * | * | * |
Input conditions¶
The study relies on a set of input conditions for the network which should trigger cell type transdifferentiation. They are specified in the Table 3 of article, reproduced herebelow:
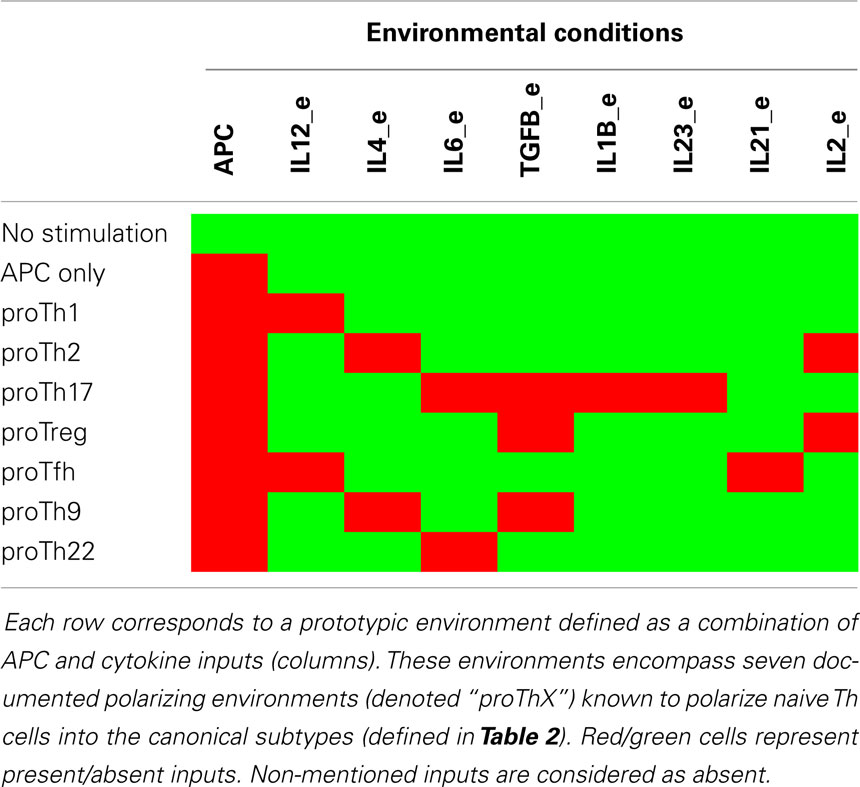
Warning The proTh9 condition requires an active IL15_e, which is not mentioned in the paper. Without it, there is no stable state matching with the condition, which seems a mistake.
conditions = {
"idle": set(),
"APC": {"APC"},
"proTh1": {"APC", "IL12_e"},
"proTh2": {"APC", "IL4_e", "IL2_e"},
"proTh17": {"APC", "IL6_e", "TGFB_e", "IL1B_e", "IL23_e"},
"proTreg": {"APC", "TGFB_e", "IL2_e"},
"proTfh": {"APC", "IL12_e", "IL21_e"},
"proTh9": {"APC", "IL4_e", "TGFB_e", "IL15_e"}, # warning IL15_e is necessary!
"proTh22": {"APC", "IL6_e"},
}
condition_nodes = reduce(set.union, conditions.values())
# sanity check
for nodes in conditions.values():
assert set(nodes).issubset(inputs), \
"unknown nodes in {}".format(nodes)
def condition_cfg(t):
return dict([(n, 1) for n in conditions[t]] \
+ [(n, 0) for n in (inputs - set(conditions[t]))])
conditions = dict([(c, condition_cfg(c)) for c in conditions])
# display
ecolumns = ["APC","IL12_e","IL4_e","IL6_e","TGFB_e","IL1B_e","IL23_e","IL21_e","IL2_e","IL15_e"]
key_conditions = list(conditions.keys())
df = pd.DataFrame([conditions[c] for c in key_conditions], index=key_conditions, columns=ecolumns)
colordf(df)
| APC | IL12_e | IL4_e | IL6_e | TGFB_e | IL1B_e | IL23_e | IL21_e | IL2_e | IL15_e | |
|---|---|---|---|---|---|---|---|---|---|---|
| idle | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| APC | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| proTh1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| proTh2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| proTh17 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| proTreg | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| proTfh | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| proTh9 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| proTh22 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Reprogramming graph¶
The core of the study lies on the prediction of reprogramming conditions accross the different subtypes. It results in a graph given in the Figure 3 of article, reproduced herebelow:
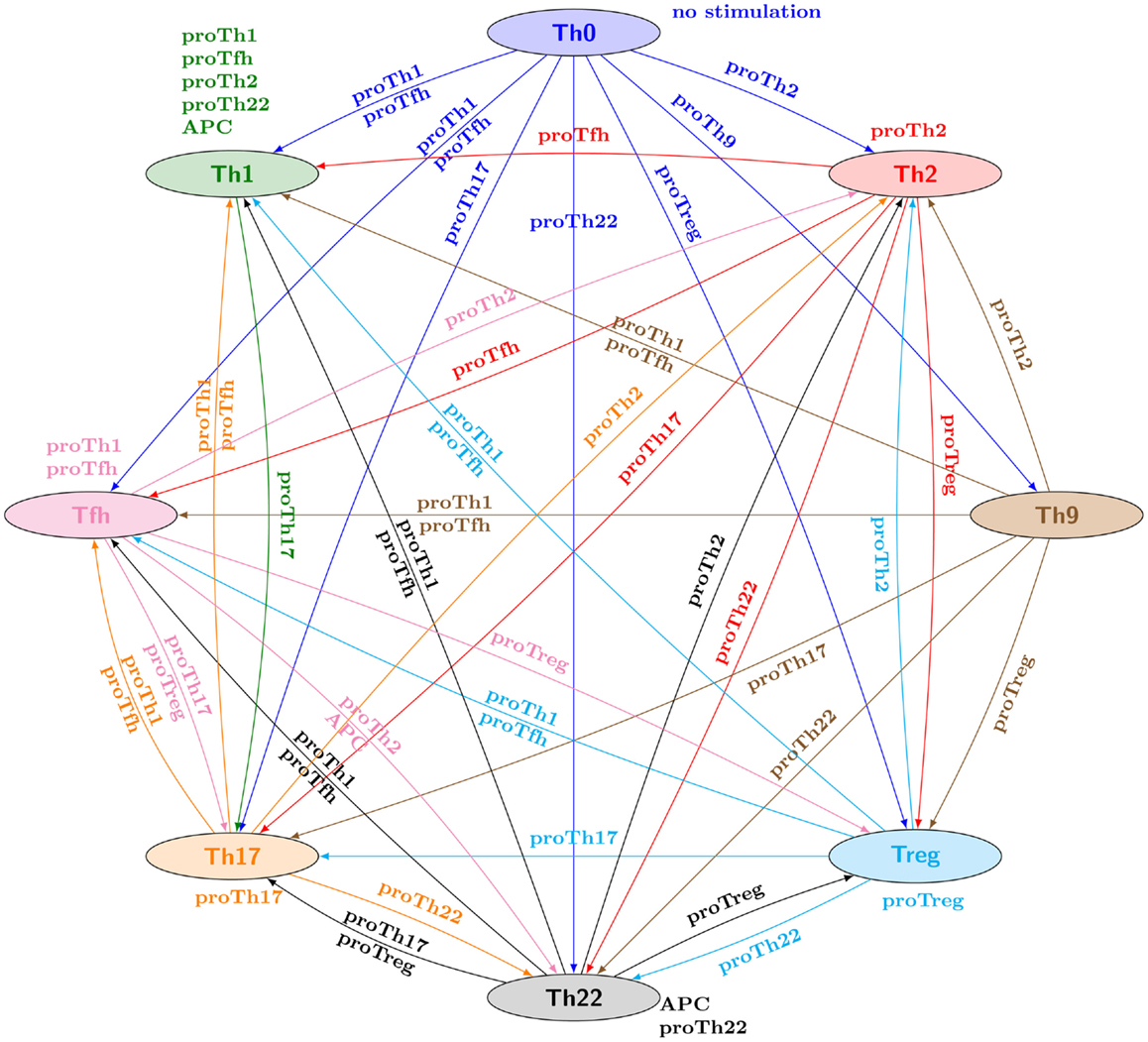
There is an edge from type T1 to T2 labeled with an input condition E whenever from any configuration matching with T1 markers there exists a path to an attractor matching with T2 under the steady input condition E.
The cell below lists the reprogramming paths of the above graph.
orig_reprogramming = {'Th0': {
'Th1': {'proTfh', 'proTh1'},
'Tfh': {'proTfh', 'proTh1'},
'Th9': {'proTh9'},
'Th2': {'proTh2'},
'Th17': {'proTh17'},
'Treg': {'proTreg'},
'Th22': {'proTh22'}},
'Th1': {
'Th1': {'APC', 'proTfh', 'proTh1', 'proTh2', 'proTh22'},
'Th17': {'proTh17'}},
'Th2': {
'Th2': {'proTh2'},
'Th1': {'proTfh'},
'Tfh': {'proTfh'},
'Th17': {'proTh17'},
'Treg': {'proTreg'},
'Th22': {'proTh22'}},
'Tfh': {
'Tfh': {'proTfh', 'proTh1'},
'Th22': {'APC', 'proTh22'},
'Th2': {'proTh2'},
'Th17': {'proTh17', 'proTreg'},
'Treg': {'proTreg'}},
'Th17': {
'Th17': {'proTh17'},
'Th22': {'proTh22'},
'Th1': {'proTfh', 'proTh1'},
'Tfh': {'proTfh', 'proTh1'},
'Th2': {'proTh2'}},
'Treg': {
'Treg': {'proTreg'},
'Th1': {'proTfh', 'proTh1'},
'Tfh': {'proTfh', 'proTh1'},
'Th2': {'proTh2'},
'Th17': {'proTh17'},
'Th22': {'proTh22'}},
'Th9': {
'Th2': {'proTh2'},
'Th1': {'proTfh', 'proTh1'},
'Tfh': {'proTfh', 'proTh1'},
'Th17': {'proTh17'},
'Th22': {'proTh22'},
'Treg': {'proTreg'}},
'Th22': {
'Th22': {'APC', 'proTh22'},
'Th1': {'proTfh', 'proTh1'},
'Tfh': {'proTfh', 'proTh1'},
'Th2': {'proTh2'},
'Th17': {'proTh17', 'proTreg'},
'Treg': {'proTreg'}}}
Analysis with MPBNs¶
Model import and helper functions¶
We convert the Boolean model to MPBN.
mbn = mpbn.MPBooleanNetwork(bn)
Herebelow are helper functions for the analysis.
def apply_condition(cfg, c):
ccfg = cfg.copy()
for n, v in conditions[c].items():
ccfg[n] = v
for n in [n for n, v in ccfg.items() if v == '*']:
del ccfg[n]
return ccfg
def trigger_subtype(t, c):
return apply_condition(subtypes[t], c)
def match_subtype(cfg, t):
markers = subtypes[t]
cyclic = []#[n for (n,v) in cfg.items() if v == '*']
if cyclic:
cfg = cfg.copy()
for n in cyclic:
cfg[n] = markers.get(n)
return set(markers.items()).issubset(set(cfg.items()))
def label_subtype(cfg):
for t in subtypes:
if match_subtype(cfg, t):
return t
def labels(a_it):
ls = set([label_subtype(a) for a in a_it])
ls.discard(None)
return ls
Computation of attractors¶
Let us first compute the list of attractors under each defined conditions:
%time attractors = \
dict([(c, list(mbn.attractors(constraints=conditions[c]))) for c in conditions])
CPU times: user 75.5 ms, sys: 226 µs, total: 75.7 ms Wall time: 75.4 ms
To analyse the nature of attractors, we filter the fixed point from the above list.
fixpoints = dict([(c, [x for x in ts if "*" not in x.values()]) \
for (c,ts) in attractors.items()])
For each condition, we display the count of attractors, and the count of fixed points.
dict([(c, (len(attractors[c]),len(fixpoints[c]))) for c in conditions])
{'idle': (8, 8),
'APC': (7, 6),
'proTh1': (5, 4),
'proTh2': (6, 6),
'proTh17': (1, 1),
'proTreg': (6, 6),
'proTfh': (3, 3),
'proTh9': (5, 5),
'proTh22': (3, 3)}
It results that all the attractors of the idle, proTh2, proTh17, proTreg, proTfh, proTh9, proTh22 are only fixed points and are thus equivalent with asynchronous interpretation. For APC and proTh1, one complex attractor is found, which translates in at least one complex asynchronous attractor.
We now classify the attractors by subtype, and display their count.
attractors_by_subtype=dict([(t,[]) for t in subtypes])
for ts in attractors.values():
for x in ts:
t = label_subtype(x)
if t is None:
continue
attractors_by_subtype[t].append(x)
attractors_by_subtype["Th0"].append(subtypes["Th0"])
dict([(t,len(ts)) for (t,ts) in attractors_by_subtype.items()])
{'Th0': 1,
'Th1': 9,
'Th2': 2,
'Th17': 3,
'Treg': 2,
'Tfh': 2,
'Th9': 1,
'Th22': 2}
Computation of the reprogramming graph¶
We divide the assessment of reprogramming paths from subtypes T1 to T2 under input conditions E in two steps:
- we first consider initial configurations which are in an attractor of T1, and check whever applying E enable the reachability of an attractor of T2;
- if true, we look for counter examples where there exists an initial configuration matching T1 but not necessarily in an attractor which cannot reach an attractor of T2.
Step 1¶
The algorithm of step 1 is the following:
- for each subtype t
- for each input condition c
- for each attractor x of subtype t
- compute the reachable attractors from a configuration matching with x with condition c
- assign the subtype for each reached attractor (ls[x])
- there is an edge from t to l with label c whenever the type l has been always reached
- for each attractor x of subtype t
- for each input condition c
Notice the computation time.
%%time
rg = {}
for t in subtypes:
rg[t] = {}
for c in conditions:
if c == "idle":
continue
ls = [labels(mbn.attractors(reachable_from=apply_condition(x,c))) \
for x in attractors_by_subtype[t]]
if not ls:
continue
ls = reduce(set.intersection, ls)
for l in ls:
if l not in rg[t]:
rg[t][l] = set()
rg[t][l].add(c)
CPU times: user 1.9 s, sys: 10.1 ms, total: 1.91 s Wall time: 1.91 s
Step 2¶
The authors of the original study consider any initial configuration matching a subtype T1, not necessarily those belonging to an attractor of T1. Therefore, the graph computed above can be over-estimated: there may exists non-stable configurations matching with T1 where applying the condition E does not lead to the subtype T2.
To find such counter-examples, we rely on a preview of an in-development tool which provides more features than the simple mpbn library.
try:
import bonesis
except:
import os
print("installing bonesis preview")
os.system("pip install --no-cache --user bonesis-preview-20200701.zip")
import importlib
importlib.invalidate_caches()
def has_nonreach(t1, e, t2):
"""
Returns True whenever there exists a configuration matching with t1
for which none of the attractor of t2 are reachable when applying conditin e
"""
# bonesis setup
data = {
"init": apply_condition(subtypes[t1], e)
}
for i, cfg in enumerate(attractors_by_subtype[t2]):
data[f"dest{i}"] = cfg
bo = bonesis.BoNesis(mbn, data)
bo.aspmodel.constants["bounded_nonreach"] = 1 # targets are in attractors
cfg = +bo.obs("init") # there exists a configuration..
for i in range(len(attractors_by_subtype[t2])):
cfg / +bo.obs(f"dest{i}")
return bo.is_satisfiable()
%%time
for c1 in rg:
ftodel = []
for c2, es in rg[c1].items():
todel = []
for e in es:
if has_nonreach(c1, e, c2):
todel.append(e)
print(f"counter-example found for {c1} -({e})-> {c2}")
for e in todel:
es.remove(e)
if not es:
ftodel.append(c2)
for c2 in ftodel:
del rg[c1][c2]
counter-example found for Th17 -(APC)-> Th22 counter-example found for Th17 -(proTreg)-> Th17 counter-example found for Th17 -(proTh9)-> Th17 counter-example found for Tfh -(proTh2)-> Th1 counter-example found for Tfh -(proTh22)-> Th1 counter-example found for Tfh -(APC)-> Th1 counter-example found for Tfh -(proTh9)-> Th17 counter-example found for Th9 -(proTh9)-> Th9 counter-example found for Th22 -(proTh9)-> Th17 CPU times: user 3.32 s, sys: 40.2 ms, total: 3.36 s Wall time: 3.34 s
Summary¶
Let us now compare the obtained graph with the graph from the original study:
rg == orig_reprogramming
True