Introduction¶
Linear polymers are molecules which form in long chains of basic units called monomers, and the chains can get as long as $10^{5}$ monomers. Real linear polymer chains can be seen in Fig. 1. Polymer scientists want to know how many different configurations an $n$-monomer chain can adopt, and also how far apart the endpoints of the polymer typically are, assuming each configuration is equally likely [1]. These questions translate into questions about self-avoiding walks, which is what we will look at in this notebook.
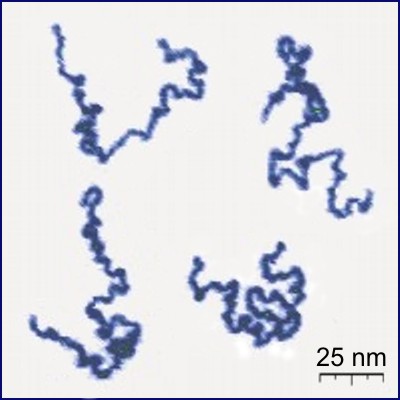
Figure 1: Appearance of real linear polymer chains as recorded using an atomic force microscope on a surface, under liquid medium. Chain contour length for this polymer is ~204 nm; thickness is ~0.4 nm. Taken from [2].
A self-avoiding walk is a path on a lattice that does not visit the same site more than once. Although simple, many questions concerning this model is difficult to answer in a rigorous mathematical fashion. In particular, there are the questions of how far an $n$-step self-avoiding walker typically travels from his starting point, or how many such walks there are [1]. Father and son P. C. Hemmer and S. Hemmer published a brief article in 1984 with the self-explanatory title An average self-avoiding random walk on the square lattice lasts 71 steps [3]. In the following we will with only a few lines of code show how they came to their conclusion.
A self-avoiding random walker¶
On the square lattice in two dimensions a self-avoiding random walker may get trapped. This is exemplified by the walks shown in Fig. 2. The figure shows all possible self-trapped walks consisting of seven, eight or nine steps.

Figure 2: Self-trapped walks with seven, eight or nine steps. Adapted from [3].
Say that in each step equal probability is given for jumping to the neighbor sites that have not been visited before. For low $n$, the probability $t(n)$ for self-trapping to occur after $n$ steps for 1 through 9 steps is:
$$ t(1) = ... = t(6) = 0; \:\: t(7) = \frac{2}{729}; \\ t(8) = \frac{5}{2187}; \:\: t(9) = \frac{31}{6561}. $$These distributions $t(n)$ can be calculated by performing a sufficiently large number of self-avoiding random walks on the lattice. For each step, which site the walker ends up moving to is decided by a random sampling.
Implement random walker function¶
We save two arrays. The number of steps of each walk is written to the array walk_lengths, while the distance $R$ between the trapped walker and its starting point is written to the array displacements.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import progressbar
import warnings
warnings.filterwarnings('ignore')
newparams = {'font.size': 20, 'lines.linewidth': 2, 'figure.figsize': (14, 7) }
plt.rcParams.update(newparams)
def random_walk2D(m, walks):
"""Perform self-avoiding random walks on an m-by-m (square) lattice.
Parameters:
m: int. Dimension of lattice.
walks: int. Number of walks to perform.
Returns:
walk_lengths: list. List of lengths of each walk.
displacements: list. List of displacement from starting point of each walk.
"""
walk_lengths = [0]*walks
displacements = [0]*walks
# Create a progress bar for the for loop
bar = progressbar.ProgressBar()
for i in bar(range(walks)):
# Create an m-by-m array (lattice) with all elements set to zero
a = np.zeros([m, m], dtype='Bool')
# Index the array using integer numbers. Walker starts in the
# middle of the array.
x = int(m/2)
y = int(m/2)
steps = 0
while (x > 0) and (x < m-1) and (y > 0) and (y < m-1):
# Check if trapped. If not, make a random move.
a[x][y] = 1
if a[x-1][y] and a[x+1][y] and a[x][y-1] and a[x][y+1]:
walk_lengths[i] = steps
# Calculate displacement from starting point
displacements[i] = np.sqrt((x - int(m/2))**2 + (y - int(m/2))**2)
break
# Random sampling
r = np.random.randint(1, 5)
if (r == 1) and (not a[x+1][y]):
x += 1
steps += 1
elif (r == 2) and (not a[x-1][y]):
x -= 1
steps += 1
elif (r == 3) and (not a[x][y+1]):
y += 1
steps += 1
elif (r == 4) and (not a[x][y-1]):
y -= 1
steps += 1
return walk_lengths, displacements
A sufficiently large square lattice is needed for the random walker not to walk off it. But a larger lattice will lead to a longer computation time. Previous runs have shown that the largest displacements usually are within a radius of 100 lattice points. Thus, it will be sufficient to define a lattice $m \times m$ of 200 $\times$ 200. If a walker should stray off this lattice, it gets a length of zero steps. As shown in Fig. 2, the fewest steps a random walker can trap itself in is seven. To check if our lattice is large enough we can thus check the shortest walk, and increase the lattice size if the shortest walk is zero.
Perform walks¶
In their paper, the Hemmers performed 60 000 walks and plotted the distribution of the probability $t(n)$ for self-trapping to occur after $n$ steps. Let us do the same and compare our results with theirs.
m = 200
walks = 60000
walk_lengths, displacements = random_walk2D(m, walks)
np.min(walk_lengths)
100% (60000 of 60000) |###################| Elapsed Time: 0:00:18 Time: 0:00:18
7
# Plot the probability distribution
plt.hist(walk_lengths, bins=np.max(walk_lengths), normed=True, color='k', label='Probabilities');
plt.xlabel('$n$');
plt.ylabel('$t(n)$');
plt.xlim([0, 300]);
# Plot the gross features of the distribution in an approximate formula
n = np.linspace(0, 300, 1000)
plt.plot(n, 0.37e-2*(n - 6)**(3/5)*np.exp(-n/40), label='Approximation');
plt.legend();
The gross features of our distribution can be expressed by approximate formulae, e.g. [3]
$$ t(n) \propto (n-6)^{3/5}e^{-n/40}. $$Adding a scaling factor of $0.37\cdot10^{-2}$ fits the approximation to our data. The approximation is shown in the plot above.
We can now from the arrays walk_lenghts and displacements calculate the average walk length with standard deviation, the most probable length, the maximum length, the average displacement from the starting point and the maximum displacement from the starting point.
# Calculate parameters
mean_len = np.mean(walk_lengths)
std_len = np.std(walk_lengths)/np.sqrt(walks)
most_prob_len = np.bincount(walk_lengths).argmax()
max_len = np.max(walk_lengths)
mean_dis = np.mean(displacements)
std_dis = np.std(displacements)/np.sqrt(walks)
max_dis = np.max(displacements)
print('An average self-avoiding random walk on the square lattice lasts %.1f ± %.1f steps (70.7 ± 0.2).'
% (mean_len, std_len))
print('Most probable length: %i (33).' % most_prob_len)
print('Maximum length: ', (max_len))
print('Average displacement R = %.2f ± %.2f (11.87 ± 0.05).' % (mean_dis, std_dis))
print('Maximum displacement: %.2f.' % (max_dis))
An average self-avoiding random walk on the square lattice lasts 70.8 ± 0.2 steps (70.7 ± 0.2). Most probable length: 29 (33). Maximum length: 463 Average displacement R = 11.87 ± 0.04 (11.87 ± 0.05). Maximum displacement: 85.91.
The Hemmers' results are in parantheses above. Ours are fairly close to the results in the paper.
Further questions¶
- How does the probability distribution for the displacement look?
- What other properties can be studied?
- How does a self-avoiding random walker behave on a hexagonal lattice?
- Or in three dimensions?
References¶
[1] Neal, M and Slade, G. The self-avoiding walk. Springer Science & Business Media, 2013.
[2] Roiter, Y and Minko, S. AFM Single Molecule Experiments at the Solid-Liquid Interface: In Situ Conformation of Adsorbed Flexible Polyelectrolyte Chains, Journal of the American Chemical Society, vol. 127, iss. 45, pp. 15688-15689 (2005).
[3] Hemmer, S and Hemmer, P C. An average self-avoiding random walk on the square lattice lasts 71 steps. J. Chem. Phys 81 (1), 1 July 1984.