The Cavendish Experiment¶
Examples - Mechanics¶
Last edited: March 15th 2018 ___Introduction¶
Newton's law of gravitation states that the force between two point masses is proportional to the product of their masses and inversely proportional to the square of the distance between them. This can be written as
\begin{equation} F= G\frac{m_1m_2}{r^2}, \label{eq:newton_grav} \end{equation}where $m_1$ and $m_2$ is the masses of the particles, $r$ is the distance between them and $G$ is some constant known as the gravitational constant. The force is directed along the line intersecting the point masses. It can be shown that this law holds for all spherically symmetric mass distributions, such as solid balls. The equation above can even be applied to the gravitational pull between stars and other celestial bodies with high accuracy! The current recommended value by CODATA for the gravitational constant is $(6.674 08 \pm 0.000 31)\cdot 10^{-11} \text{Nm$^2$/kg$^2$}$ [1]. This is a small number, and measuring the gravitational constant thus requires extremely precise equipment.
The first direct laboratory measurement of the gravitational constant was performed in 1798 by Henry Cavendish [2]. The apparatus in the original experiment consisted of a 1.8 meter long wooden arm with two lead balls about 5 cm in diameter attached on either side. The wooden arm was suspended in a horizontal position from a 1 meter long wire. This is known as a torsion pendulum. Two large lead balls was used to exert a gravitational pull on the torsion pendulum, making it rotate. Due to the torque in the wire, the pendulum began to oscillate around its new equilibrium position.
A similar experiment is performed by all first year physics students at NTNU. In this notebook we will discuss the Cavendish experiment. We will create a model that describes the oscillation of the torsion pendulum and by using curve fitting on a set of measurements, we will estimate the period of the oscillation and its equilibrium position. This will in turn be used to estimate the gravitational constant. The theory section is to a large extent based on the laboratory manual used in the course FY1001 Mechanical Physics at NTNU (see ref. [3]). We start by briefly discussing experimental setup (we refer to the Laboratory Manual for a more complete review of the experiment).
Experimental Setup¶
The apparatus used at NTNU is similar to the one used by Cavendish. The experiment is in principle performed in the following way. The two large lead balls of mass $M$ are set in position 1, as shown in figure 1. The torsion pendulum will begin to oscillate around some equilibrium angle $\theta_1$. A laser beam is reflected on a mirror attached to the torsion pendulum, and hits a ruler at a position $S(t)$. The position on the ruler is recorded every 30 seconds. When the system is at rest, the lead spheres are set in position 2, making the pendulum oscillate around $\theta_2$.
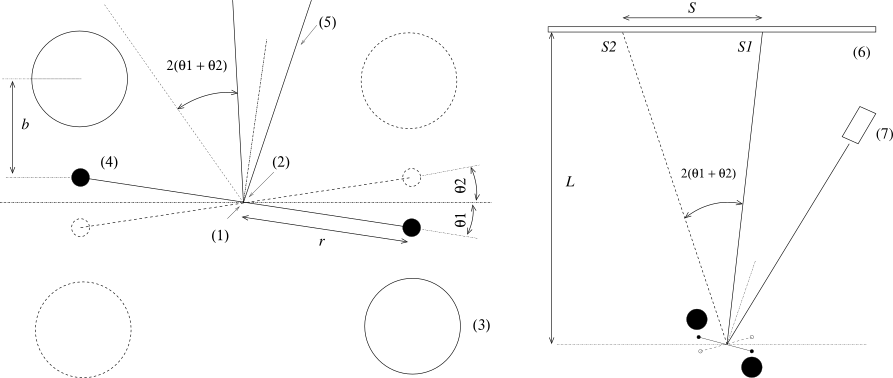
Figure 1. The figure to the left is a schematic diagram of the torsion pendulum used in the experiment, directed along the torsion wire. (1) Torsion wire, (2) mirror, (3) large lead balls, (4) small lead balls, (5) laser beam. The entire setup can be seen in the figure to the right. Position 1 is shown in solid lines and position 2 is shown in dashed lines. The equilibrium position in the absence of the large lead balls is along the horizontal dotted line. The figures are taken from the Laboratory Manual in the course F1001 Mechanical Physics at NTNU (ref. [2]).
Let's import needed packages and set common figure parameters before we proceed to derive a model that describes the damped oscillation of the pendulum.
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
%matplotlib inline
# Set some figure parameters
newparams = {'figure.figsize': (18, 9), 'axes.grid': False,
'lines.markersize': 6, 'lines.linewidth': 2,
'font.size': 15, 'mathtext.fontset': 'stix',
'font.family': 'STIXGeneral'}
plt.rcParams.update(newparams)
Model¶
As mentioned in the introduction, Cavendish used a torsion pendulum (also called a torsion balance) in his measurements. When the rotational angle (the torsion angle) $\theta$ is small, its torque $\vec \tau = \vec F\cdot\vec r$ is approximately proportional to $\theta$. That is,
\begin{equation} \label{eq:torsion_pendulum} \tau_1 =-D\theta, \end{equation}for some constant $D$, called the torsion constant. This is analogous to Hooke's law for a spring.
The air resistance of an object is approximately proportional to the velocity at small velocities. This relation is called Stoke's law. The torque due to air resistance is thus proportional to the angular velocity $\dot \theta$. That is,
\begin{equation} \tau_2 = -b\dot\theta. \label{eq:air_resistance} \end{equation}We neglect friction in the torsion wire.
Newton's second law for rotation reads,
\begin{equation} \sum \tau_i = I\ddot\theta, \label{eq:N2_rotation} \end{equation}where $I$ is the moment of inertia, in our case given by $I=2mr^2$ (two spherically symmetric masses $m$ at a distance $r$ from the reference point). By combining the equations \eqref{eq:torsion_pendulum}, \eqref{eq:air_resistance} and \eqref{eq:N2_rotation}, we obtain the differential equation
\begin{equation} I\ddot\theta + b\dot\theta+D\theta = 0, \label{eq:diff_eq} \end{equation}which describes the oscillation of the torsion pendulum. The general solution can in this case be written as
\begin{equation} \theta(t) = \theta_0 e^{-\alpha t}\sin\left(\omega t+\phi\right), \label{eq:model_theta} \end{equation}where $\theta_0$ is the initial amplitude, $\phi$ is some phase factor, $\omega\equiv\sqrt{\omega_0^2-\alpha^2}$, $\alpha \equiv b/2I$ and $\omega_0 \equiv\sqrt{D/I}$. The oscillation is in our case underdamped (see e.g. [4] for more information), which means that $\omega^2 = \omega_0^2-\alpha^2>0$. This is confirmed by the measured data.
In the actual experiment we do not measure $\theta$, but $S$ as a position of the laser beam on a ruler (see figure 1). The position $S$ is given by
\begin{equation} S/L=\tan\theta\approx \theta \label{eq:S_approx} \end{equation}when $L\ll S$ (see exercise 1). We therefore obtain
\begin{equation} S(t) = S_0 + A e^{-\alpha t}\sin\left(\omega t + \phi\right). \label{eq:model_S} \end{equation}def osc(t, S_0, A, alpha, omega, phi):
# Model for harmonic oscillations
return S_0 + A*np.exp(-alpha*t)*np.sin(omega*t + phi)
Curve fitting¶
The period of the oscillation is $T=2\pi/\omega$. The parameters $\phi$, $\omega$, $\alpha$, $A$ and $S_0$ can be estimated using curve fitting of the model on the measured data. There are several ways to perform curve fitting in Python. In this notebook we will be using optimize.curve_fit from SciPy, which uses non-linear least squares to fit a function to data. The function has three input parameters: the model function (osc), the measured $x$-data (t) and the measured $y$-data (S). In addition, we will use the optional argument p0, which is the initial guess for the parameters. The function returns an array of the optimal values for the parameters (params) and a corresponding covariance matrix (cov). The diagonals of the covariance matrix provide the variance of the parameter estimates. The standard deviation is in turn given by the square root of the variances.
def fit(S, t, params_init=[1,1,1,1,1]):
""" Performs curve fitting of the function osc() on the data points
stored in S.
Parameters:
S: array-like vector, len(N). The measured displacement
as a function of time.
t: array-like vector, len(N). Time corresponding to the
measurements in S.
params_init: Initial guess for the parameters.
Returns:
params: Parameters which minimizes the quadratic error (best fit).
cov: Covariance matrix for the parameters.
"""
try:
params, cov = curve_fit(osc, t, S, p0=params_init)
return params, cov
# curve_fit will return a RuntimeError if it can't estimate the parameters.
except RuntimeError as err:
print("Fit failed.")
return params_init, np.zeros(len(params_init), len(params_init))
# Read data from file with time in minutes in first column, time in
# seconds in second column and swing in third column
# Position 1
data = np.loadtxt('S1data.txt')
t1data = data[:, 0]*60 + data[:, 1]
S1data = data[:, 2]*0.001 # m
# Position 2
data = np.loadtxt('S2data.txt')
t2data = data[:, 0]*60 + data[:, 1]
S2data = data[:, 2]*0.001 # m
We are now ready to perform the curve fit!
# Initial values for fit (educated guesses)
S0_0 = 3.50e+00 # Equilibrium line
A0 = 0.3 # Amplitude, swing
Alpha0 = 0.001 # Exponential damping coefficient for the amplitude
T0 = 600 # Swing period
phi0 = 0 # Phase angle
params_init = [S0_0, A0, Alpha0, 2*np.pi/T0, phi0]
# Fit model parameters to data
params1, cov1 = fit(S1data, t1data, params_init) # POSITION 1
err1 = np.sqrt(np.diag(cov1))
params2, cov2 = fit(S2data, t2data, params_init) # POSITION 2
err2 = np.sqrt(np.diag(cov2))
Let's make a plot!
# Position 1
t = np.linspace(t1data[0], t1data[-1], 200)
plt.plot(t, params1[0]*np.ones(len(t)), '--', color='0.6')
plt.plot(t, osc(t, *params1), '-', color=(.5,.5,1), label='Fit position 1')
plt.plot(t1data, S1data, 'o', color=(0,0,1), label='Position 1 data')
# Position 2
t = np.linspace(t2data[0], t2data[-1], 200)
plt.plot(t, params2[0]*np.ones(len(t)), '--', color='0.6')
plt.plot(t, osc(t, *params2), '-', color=(1,.5,.5), label='Fit position 2')
plt.plot(t2data, S2data, 'o', color=(1,0,0), label='Position 1 data')
plt.xlabel('Time, (s)')
plt.ylabel('Displacement, (mm)')
plt.legend(loc='best')
plt.show()
The Gravitational Constant¶
Deriving an Expression for the Gravitational Constant¶
Consider for the moment only the gravitational force $F_0$ between the large lead balls and the nearest small balls (that is, neglect $f$ in figure 2). From figure 2 it is clear that the torque on the pendulum due to the gravitational force $F_0$ must be equal to the torque due to the torsion wire (equation \eqref{eq:torsion_pendulum}) at equilibrium (when the system is at rest). That is $2F_0r=D\theta_1=D\theta_2$. By making use of equation \eqref{eq:S_approx}, we obtain
\begin{equation} F_0 = \frac{D}{r}\cdot\frac{\theta_1+\theta_2}{4}\approx \frac{D}{r}\cdot\frac{S}{4L}. \label{eq:F0} \end{equation}
Figure 2. The large ball acts on the nearest small ball with a gravitational force $F_0$. There is also a gravitational pull $F_0'$ from the opposite large ball with a component $f$ that reduces the total torque on the pendulum. The figure is taken from the Laboratory Manual in the course F1001 Mechanical Physics at NTNU (ref. [2]).
We assume for simplicity that $\sqrt{\omega_0^2-\alpha^2}\approx \omega_0=\sqrt{D/I}$ in equation \eqref{eq:model_theta} (see exercise 2 and 3). The torsion constant can in this case be written as
\begin{equation} D = \frac{4\pi^2 I}{T^2}. \label{eq:torsion_const} \end{equation}If we insert equation \eqref{eq:F0} and \eqref{eq:torsion_const} and $I=2mr^2$ into Newton's law of Gravitation \eqref{eq:newton_grav} and solve for $G$, we obtain
\begin{equation} G = \frac{r^2}{F_0mM}=\frac{\pi^2b^2rS}{T^2LM}, \label{eq:grav_const} \end{equation}where $m$ is the mass of the small lead balls, $M$ is the mass of the large lead balls and $b$ is the distance between the masses $m$ and $M$. Note that $m$ is canceled in the final expression.
The component $\vec f$ of $\vec F_0'$ parallel to $\vec F_0$ lowers the total torque on the pendulum and gives a small correction to equation \eqref{eq:grav_const}. From figure 2 is is clear that
$$f = F_0'\cdot\frac{b}{r'},$$where $r'=\sqrt{b^2+4r^2}$ is the distance between the balls. If we insert this into the Newton's law of Gravitation \eqref{eq:newton_grav}, we obtain
$$f = G\frac{mM}{b^2+4r^2}\cdot\frac{b}{\sqrt{b^2+4r^2}}= G\frac{mM}{b^2}\cdot\frac{b^3}{(b^2+4r^2)^{3/2}}=F_0\cdot \beta,$$where $\beta\equiv b^3/(b^2+4r^2)^{3/2}$. The total force on each of the small balls are thus $F' = F_0-f = F_0(1-\beta)$. By comparing with equation \eqref{eq:grav_const}, we a corrected expression for the gravitational constant,
\begin{equation} G = \frac{1}{1-\beta}\cdot\frac{\pi^2b^2rS}{T^2LM}. \label{eq:grav_const_corr} \end{equation}Estimating the Gravitational Constant¶
$L$, $M$, $b$ and $r$ is found by measuring on the apparatus used in the experiment. The measured quantities corresponding to the data used in this notebook are defined in the following code snippet.
We store these quantities as arrays of length 2, with the first position being the value and the second position being the uncertainty.
b = [0.042, 0.001 ] # m
r = [0.050, 0.0001] # m
L = [2.265, 0.01 ] # m
M = [1.493, 0.002 ] # kg
In addition, we need to extract the difference in equilibrium positions $S=|S_{01}-S_{02}|$ and the period $T$ from the curve fit performed earlier.
We can extract $T_1$, $T_2$, $S_{01}$ and $S_{02}$ and their standard deviations (uncertainties) from params1, err1, params2 and err2. The period is given by $T_i=2\pi/\omega_i$, and their uncertainties are related by $\Delta T/T = \delta \omega/\omega\Rightarrow \Delta T = \Delta\omega\cdot2\pi/\omega^2$.
S01 = (params1[0], err1[0])
S02 = (params2[0], err2[0])
print("S01 = ( %.4f ± %.5f ) mm"%(S01))
print("S02 = ( %.4f ± %.5f ) mm"%(S02))
T1 = (2*np.pi/params1[3], 2*np.pi/params1[3]**2*err1[3])
T2 = (2*np.pi/params2[3], 2*np.pi/params2[3]**2*err1[3])
print("T1 = ( %.2f ± %.2f ) s"%(T1))
print("T2 = ( %.2f ± %.2f ) s"%(T2))
S01 = ( 0.3587 ± 0.00025 ) mm S02 = ( 0.4471 ± 0.00020 ) mm T1 = ( 651.53 ± 3.02 ) s T2 = ( 636.84 ± 2.88 ) s
The physical setup is the same in position 1 and position 2, and we would therefore expect that $T_1\approx T_2$. Note however that the estimated values of $T_1$ and $T_2$ differs by almost 15 seconds. This indicates that the uncertainty in the period is larger than the standard deviation in the fit. We will therefore use $$T = (T_1+T_2)/2, \qquad\Delta T = |T_2-T_1|/2,$$ as the period of the oscillations and its uncertainty.
The only error estimate we have for the equilibrium positions $S_{01}$ and $S_{02}$ are the standard deviation from the fit. We will therefore use $$S = |S_{02} - S_{01}|,\qquad \Delta S = \sqrt{\Delta S_{01}^2 + \Delta S_{01}^2}.$$
Note that we have not taken errors in the measurements into count. Better results for the uncertainties is obtained if the experiment is repeated.
S = (abs(S01[0] - S02[0]), (S01[1]**2 + S02[1]**2)**.5)
print("S = ( %.2e ± %.1e ) mm"%(S))
T = ((T1[0] + T2[0])/2, abs(T1[0] - T2[0])/2)
print("T = ( %.2f ± %.2f ) s"%(T))
S = ( 8.84e-02 ± 3.2e-04 ) mm T = ( 644.19 ± 7.34 ) s
We now insert these quantaties into equation \eqref{eq:grav_const_corr} in order to estimate the gravitational constant $G$.
beta = b[0]**3*(b[0]**2+4*r[0]**2)**(-3/2.)
G = 1/(1 - beta)*np.pi**2*b[0]**2*r[0]*S[0]/(T[0]**2*L[0]*M[0])
print("G = %.2e m^3/(kg s^2)"%(G))
G = 5.82e-11 m^3/(kg s^2)
This is in the same order of magnitude as the recommended value from CODATA $(6.674 08 \pm 0.000 31)\cdot 10^{-11} \text{Nm$^2$/kg$^2$}$. The gravitational constant is quite difficult to measure and the experiment is influenced by many systematic errors [5]. Moreover, the measurement was conducted during a laboratory session in a room full of people. This is not ideal conditions!
Since we have acquired the uncertainty in all the quantities used in equation \eqref{eq:grav_const_corr}, we can also compute the uncertainty in $G$. This is left as an exercise for the reader (exercise 4 and 5).
Exercises and Further Work¶
There are several exercises in the Laboratory Manual (ref. [3]). Check them out!
- How can we proceed without the approximation $S/L=\tan\theta\approx \theta$? What additional information is needed? Hint. Take a close look at figure 1. The angle between the ruler and the laser beam is in fact not known!
- Use the result to check if the approximation $\sqrt{\omega_0^2-\alpha^2}\approx \omega_0$ is valid.
- Find an expression for the torsion constant in equation \eqref{eq:torsion_const} without the approximation in exercise 3. Hint. Assume that information about the small lead balls are known.
- By only looking at equation \eqref{eq:grav_const}, which quantities are most important to measure precisely (which causes the largest error in the final expression)?
- Use the uncertainties $\Delta b$, $\Delta T$, $\Delta S$, $\Delta r$, $\Delta L$ and $\Delta M$ and equation \eqref{eq:grav_const} to find an uncertainty in the estimated value for the gravitational constant $\Delta G$. Hint. Use a formula for error propagation
Sources and Further Readings¶
[1] Mohr, Peter J., Newell, David B. & Taylor, Barry N. (2016). CODATA recommended values of the fundamental physical constants: 2014. Rev. Mod. Phys., 88, 035009. See http://www.codata.org/.
[2] Cavendish, Henry. Philosophical Transactions 17, 469 (1798). Note that the goal of the original experiment was to measure the density of the Earth. However, one can express his result in terms of the gravitational constant.
[3] Herland, Egil V., Sperstad, Iver B., Gjerden, Knut, et al.: Laboratorium i emne FY1001 mekanisk fysikk. NTNU 2016. URL: http://home.phys.ntnu.no/brukdef/undervisning/fy1001_lab/KompendiumMaster.pdf
[4] Hyperphysics.phy-astr.gsu.edu: Damped Harmonic Oscillator [Online]. http://hyperphysics.phy-astr.gsu.edu/hbase/oscda.html [retrieved Sep. 2017]
[5] Cross, William D. Systematic Error Sources in a Measurement of G using a Cryogenic Torsion Pendulum. University of California 2009. URL: http://www.physics.uci.edu/gravity/papers/WDCross%20thesis.pdf