Structures de données relationnelles : les graphes¶
On rappelle trois implémentations possible de la struture de graphe :
- sous forme de matrice d'adjacence
- sous forme de dictionnaire de listes de successeur
- sous forme de classe
On donne le graphe suivant. Ecrire sa matrice d'adjacence et son dictionnaire de listes de successeurs. On peut aussi construire une deuxième liste de successeurs du graphe en considérant qu'il n'est pas pondéré.
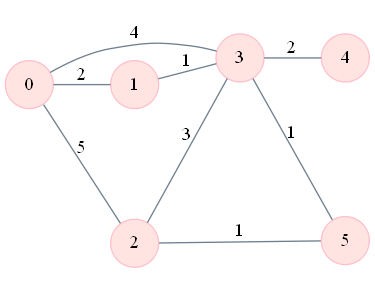
g_mat = []
g_suc = {}
g_suc_np = {}
La classe graphe est donnée ci-dessous. Créer l'objet correspond au graphe précédent.
class Node:
"""
Classe représentant les sommets d'un graphe
Attributs :
nom : le nom du sommet. Pas de type prédéfini (peut être aussi bien une chaîne qu'un entier ou autre,
cette dernière possibilité étant déconseillé ceci dit)
traité : booléen pour savoir si le sommet a été traité lors d'un parcours par exemple
"""
def __init__(self,nom):
self.nom =nom
self.traite = False
def __repr__(self):
return f' {self.nom} '
class Edge:
"""
Classe représentant les arcs d'un graphe orienté et éventuellement pondéré
Attributs :
depart, arrivee : objets de type Node (sommet), sommets de départ et d'arrivée.
poids : entier ou flottant donnat le poids de l'arête.
Pour un graphe non pondéré, on peut fixer ce poids systématiquement à 1
"""
def __init__(self, depart, arrivee, poids):
self.depart = depart
self.arrivee = arrivee
self.poids = poids
def __repr__(self):
return f' ({self.depart},{self.arrivee}, poids {self.poids})'
class Graphe:
"""
Classe implémentant un graphe. Si le graphe n'est pas orienté, il faut doubler les arcs (d -> a et a -> d)
pour obtenir un arête. Un graphe non pondéré aura tous les poids des arêtes à 1.
Attributs :
nom : chaîne (a priori), nom du graphe
listeNoeuds : liste d'objets de type Node
listeAretes : liste d'objets de type Edge
pondere : booléen Vrai si le graphe est pondéré et faux sinon
Méthodes :
addNode : ajoute un noeud de nom donné
addEdge : ajoute une arête du noeud1 vers le noeud2, de poids 1 si le grpahe n'est pas pondéeé
"""
def __init__(self, nom, pondere):
self.nom=nom
self.listeNoeuds=[]
self.listeAretes=[]
self.pondere = pondere
def addNode(self,nomNoeud):
# vérifie si le noeud du nom entré existe
for elN in self.listeNoeuds:
if nomNoeud == elN.nom:
return elN
noeud=Node(nomNoeud) # sinon le crée
self.listeNoeuds.append(noeud)
return noeud
def addEdge(self, nomNd1, nomNd2, poids = 1):
# G.addNode(nomNd1) crée le noeud dont le
# nom est passé en paramètre
Nd1=self.addNode(nomNd1)
Nd2=self.addNode(nomNd2)
for elA in self.listeAretes:
# on vérifie si l'arête est déjà là
if nomNd1 == elA.depart.nom and nomNd2 == elA.arrivee.nom:
return
arete=Edge(Nd1,Nd2,poids) # crée une arête entre Nd1 et Nd2
self.listeAretes.append(arete)
def __repr__(self):
c_s = ""
for s in self.listeNoeuds :
c_s = c_s + s.__repr__()
c_a = ""
for a in self.listeAretes :
c_a = c_a + a.__repr__() +"\n"
return "\nNom : "+ self.nom + "\nSommets : " + c_s + "\nAretes : \n" + c_a
Fonctions de conversion¶
Ecrire les fonctions permettant de passer d'une implémentation à une autre.
Au minimum : de matrice d'adjacence vers liste de successeurs, de dictionnaires de listes de successeurs vers objet. Si possible, d'objet vers matrice d'adjacence, histoire de pouvoir passer d'une représentation quelconque à n'importe quelle autre. Enfin, si vous allez vite, faites les conversions réciproques.
On pourra tester le programme avec les exemples précédemment faits.
def suc2Mat(g_s, pondere = False):
"""
Convertit le dictionnaires de listes de successeur d'un graphe
en matrice d'adjacence.
@param g_s : dictionnaire de listes de successeurs d'un graphe (orienté ou non)
@param pondere : Booléen vrai si le graphe est pondéré
@return g_m : liste de listes, matrice d'adjacence du graphe
"""
return(g_m)
def mat2Suc(g_m, pondere = False):
"""
Convertit la martrice d'adjacence d'un graphe
en dictionnaires de listes de successeur.
@param g_m : liste de listes, matrice d'adjacence d'un graphe (orienté ou non)
@param pondere : Booléen vrai si le graphe est pondéré
@return g_s : dictionnaire de listes de successeurs du graphe
"""
return(g_s)
def suc2Obj(g_s, nom, pondere = False):
"""
Convertit le dictionnaires de listes de successeur d'un graphe
en objet de type Graphe.
@param g_s : dictionnaire de listes de successeurs d'un graphe (orienté ou non)
@param nom : chaine de caractères, nom du graphe
@param pondere : Booléen vrai si le graphe est pondéré
@return g_o : objet de type Graphe
"""
return g_o
def obj2Suc(g_o):
"""
Convertit un objet de type Graphe en dictionnaires de listes de successeur du graphe
@param g_o : dictionnaire de listes de successeurs d'un graphe (orienté ou non)
@return g_s : dictionnaire de listes de successeurs du graphe
"""
return g_s
def mat2Obj(g_m, nom, pondere = False):
"""
Convertit le dictionnaires de listes de successeur d'un graphe
en objet de type Graphe.
@param g_m : liste de listes, matrice d'adjacence d'un graphe (orienté ou non)
@param nom : chaine de caractères, nom du graphe
@param pondere : Booléen vrai si le graphe est pondéré
@return g_o : objet de type Graphe
"""
return g_o
def obj2Mat(g_o):
"""
Convertit un objet de type Graphe en dictionnaires de listes de successeur du graphe
@param g_o : dictionnaire de listes de successeurs d'un graphe (orienté ou non)
@return g_m : mtrice d'adjacence du graphe
"""
return g_m
"""
assert mat2Suc(g_mat, True) == g_suc
assert suc2Mat(g_suc, True) == g_mat
assert mat2Suc(suc2Mat(g_suc_np)) == g_suc_np
print("conversion liste de successeurs -> objet")
print(suc2Obj(g_suc, "g objet",True))
print("conversion objet -> listes de successeurs")
print(g_suc)
g_s_b = obj2Suc(g_obj)
print(g_s_b)
#assert g_s_b == g_suc
# regarder la différence entre les deux représentations précédentes
print("\nconversion matrice d'adjacence -> objet")
print(mat2Obj(g_mat, "g objet",True))
print("\nconversion objet -> matrice d'adjacence")
print(g_mat)
print(obj2Mat(g_obj))
# assert obj2Mat(g_obj) == g_mat
# regarder la différence entre les deux représentations précédentes (et constater les limites des assertions)
"""
print()
Fonctions de parcours¶
Implémenter les algorithmes de parcours en largeur et en profondeur. On utilisera l'implémentation de son choix. Pour ceux qui doutent de l'implémentation à utiliser, privilégiez plutôt celle par listes de successeurs. L'algorithme est plus rapide qu'avec la matrice d'adjacence, et par ailleurs il n'y a pas à gérer l'aspect objet qui peut faire peur.
Pour la structure de pile, on pourra utiliser simplement une liste Python, avec append/poppour empiler/dépiler. Pour la structure de file, si possible utilisez la bibliothèque deque avec append/popleft pour enfiler/défiler. En cas d'allergie à cette bibliothèque, utilisez une liste Python et pop(0) pour défiler (rappel : c'est beaucoup plus lent).
from collections import deque
def dfs(g_s, depart, pondere = False):
"""
Parcours en profondeur d'un graphe donné sous forme de liste de successeurs
@param g_s : dictionnaire des listes de successeurs du graphe
@param depart : entier, sommet de départ du parcours
@param pondere : Booléen vrai si le graphe est pondéré
@return parkour_p : liste des sommets parcours en profondeur
"""
return parkour_p
def bfs(g_s, depart, pondere = False):
"""
Parcours en largeur d'un graphe donné sous forme de liste de successeurs
@param g_s : dictionnaire des listes de successeurs du graphe
@param depart : entier, sommet de départ du parcours
@param pondere : Booléen vrai si le graphe est pondéré
@return parkour_l : liste des sommets parcours en largeur
"""
return parkour_l
print("Profondeur")
print(dfs(g_suc, 0, True))
print(dfs(g_suc_np, 0))
print("Largeur")
print(bfs(g_suc, 0, True))
print(bfs(g_suc_np, 0))
Compléments¶
Pour ceux qui vont vite, programmer la recherche de cycles ainsi que celle d'un chemin entre deux sommets. On se placera dans le cas d'un graphe non pondéré.
def distances_chemin(g_s, depart, arrivee):
"""
Renvoie les distances entre le sommet de départ et tous les autres sommets,
ainsi qu'un chemin entre deux sommets d'un graphe non pondéré donné sous forme de liste de successeurs.
Ici on utilise le parcours en largeur.
@param g_s : dictionnaire des listes de successeurs du graphe non pondéré
@param depart : entier, sommet de départ du chemin
@param arrivee : entier, sommet d'arrivée du chemin
@return promenade : liste des sommets parcourus pour aller du départ à l'arrivée
@return distance : longueur du chemin en nombre d'arêtes
"""
return distances, promenade
def cycle(g_s, depart):
"""
recherche d'un cycle dans un graphe donné sous forme de liste de successeurs
Basé sur le parcours en profondeur
@param g_s : dictionnaire des listes de successeurs du graphe
@param depart : entier, sommet de départ du parcours
@return : booléen Vrai si le graphe possède au moins un cycle, faux sinon
@return pred : tableau des prédécesseurs (dans le cas où le retour vaut Vrai), None sinon
"""
return False, None
print(distances_chemin(g_suc_np, 0, 4))
print(cycle(g_suc_np, 0))
Application¶
Un critère graphe-ique de divisibilité par 7¶
Source : https://blogdemaths.wordpress.com/2013/02/02/un-critere-visuel-de-divisibilite-par-7/
Le graphe orienté suivant permet de savoir si un nombre $n$ est divisible par 7.
 Il s'utilise comme suit:
Il s'utilise comme suit:
- Partir du noeud 0
- Parcourir autant de flèches noires que le premier chiffre de $n$.
- Parcourir une flèche bleue
- S'il reste au moins deux chiffres dans $n$, supprimer le premier et boucler sur 2.
- Le nombre est divisible par 7 si et seulement si le noeud d'arrivée est 0
Tester cet algorithme à la main avec 437 et 378.
Le programmer (il est indispensable de réfléchir à l'implémentation à utiliser, on rajoutera un arc 0 -> 0). Le programme renverra la liste des sommets parcourus, et affichera le résultat sous la forme a->b->..., puis la conclusion. Tester le programme avec des grands nombres (comme 481466241735205727 ou 23197055899603)
Remarque : la méthode se généralise. Elle est justifiée ici. Voici par exemple le graphe pour la divisibilité par 13 :
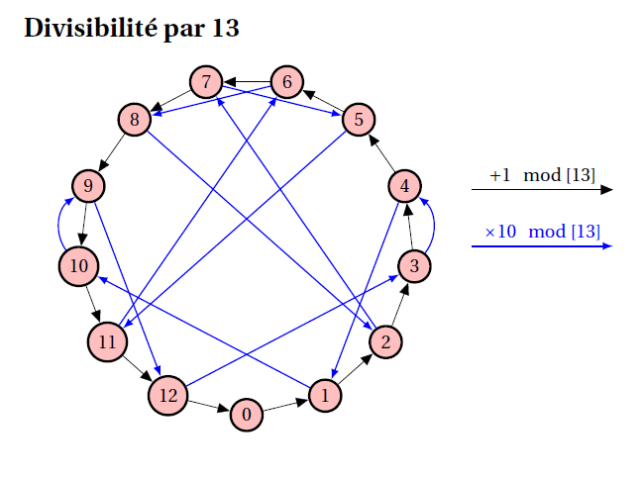

Ce(tte) œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.
frederic.mandon@ac-montpellier.fr, Lycée Jean Jaurès - Saint Clément de Rivière - France