Remarque préliminaire : Jupyter est parfois capricieux pour le téléchargement des images. Si les images n'apparaissent pas dans le notebook, chargez les dans le même dossier que le notebook. Les adresses se trouvent en double cliquant dans les cellules de texte (là où il y a précisé "image", c'est qu'il y a une image normalement...). Puis changez le code comme ceci : 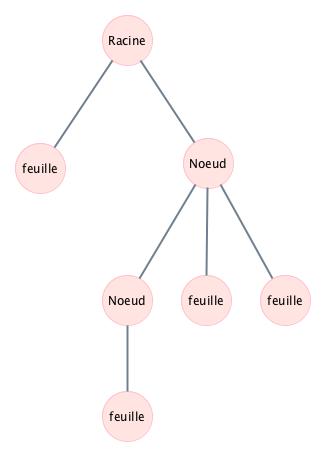 devient  ou même 
Retour sur les listes¶
Dans ce notebook, on va reprendre les listes pour résoudre de deux nouvelles manières le problème de Josèphe.
On va utiliser les listes, que l'on peut voir comme des arbres filiformes.
On rappelle les primitives sur les listes :
- test de vacuité d'une liste :
estVide(liste) - Obtention de la longueur de la liste :
longueur(liste) - Accéder au k-ième élément de la liste :
lire(liste , k) - Supprimer le k-ième élément de la liste :
supprimer(liste , k) - Insérer un élément en k-ième position dans la liste :
inserer(liste , k)
Une implémentation des listes chainées¶
Ubne liste peut être considérée comme une suite de cellules (ou noeuds), éventuellement vide (None) pour la liste vide. Chaque cellule comporte une tête (la donnée) et une queue (le suivant), qui est soit une autre liste, soit la liste vide (None, None). Pour faire le parallèle avec les arbres dégénérés, la tête correspond à la racine et la queue soit à vide(None), soit à l'unique sous-arbre, puisque qu'on se place dans le cas où l'arbre est filiforme.
Remarque : On utilise souvent tête au lieu de donnee et queue au lieu de suivant. Dans le cadre de ce TP, ces noms sont utilisés dans un autre sens pour les listes circulaires, ce qui pourrait porter à confusion.
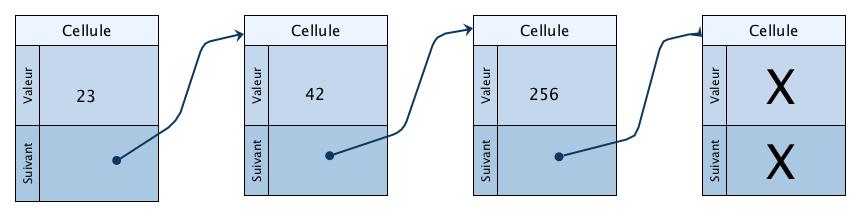
Les attributs de la classe CelluleL sont :
donnee: l'élément de tête de la liste (éventuellementNone)suivant: la liste composant la deuxième partie du noeudlongueur: on rajoute cet attribut pour plus de commodité
les méthodes sont celles données par les primitives ci-dessus.
Quelques remarques sous forme de questions :
- pourquoi est-il assez "naturel" d'utiliser des fonctions récursives, notamment pour insérer et supprimer ?
- Comment se fait-il que les longueurs des listes après insertion et suppression soient justes, alors qu'on ne modifie pas l'attribut longueur ?
Utilisations des listes chaînées¶
- piles
- allocation mémoire sur un disque dur : les blocs libres sont stockés dans une liste chaînée
- opérations arithmétiques sur des grands entiers
- page suivante/précédente sur un navigateur : on utilise une liste doublement chaînée
- idem pour un logiciel de visualisation d'images, ou d'écoute de musique
class CelluleL:
def __init__(self , donnee = None , suivant = None) :
self.donnee = donnee
if donnee is not None :
self.suivant = suivant
elif suivant is not None :
self.suivant = None
def __repr__(self):
if self.donnee is None :
return '()'
else:
# la 1ère possibilité met l'aspect récursif en avant
# la 2ème possibilité mes l'aspect chaiîné en avant
#return '(' + str(self.donnee) + repr(self.suivant).replace('None','()') + ')'
return str(self.donnee) + '->' + repr(self.suivant)
def estVide(self):
return self.donnee is None
def longueur(self):
long = 0
while not self.estVide():
long = long + 1
self = self.suivant
return long
def getMaillon(self, k):
if k > self.longueur() :
raise IndexError('Index trop grand')
else :
while k > 0:
k = k - 1
self = self.suivant
return self
def lire(self , k) :
return self.getMaillon(k).donnee
def inserer(self , k, element) :
if k > self.longueur() :
raise IndexError('Index trop grand')
elif k == 0 and not self.estVide():
return CelluleL(element,self)
elif k == 0 and self.estVide():
print("ici")
return CelluleL(element, CelluleL())
else :
maillon = self.getMaillon(k -1)
prochain = CelluleL(element,maillon.suivant)
maillon.suivant = prochain
return self
def supprimer(self , k) :
longueur_liste = self.longueur()
if k >= longueur_liste :
raise IndexError('Index trop grand')
elif k == 0 and longueur_liste == 1 :
self = CelluleL()
elif k == 0 :
self = self.suivant
else :
maillon = self.getMaillon(k - 1)
maillon.suivant = maillon.suivant.suivant
return self
Jeu de tests¶
Dans la cellule précédente, créer un jeu de tests pour les différentes méthodes. On pourra en particulier :
- créer la liste nil (vide), tester sa longueur et le fait qu'elle soit vide ;
- y ajouter un élément, puis le supprimer, et vérifier que les longueurs sont bonnes ainsi que le test de vacuité ;
- créer deux listes
1->2->3->4->5->()et5->4->3->2->1->(); - ajouter/supprimer des éléments en début, milieu et fin d'une de ces listes.
Application au problème de Josèphe¶
On rappelle le terrible problème de Josèphe. Un nombre n de soldats juifs sont positionnés en cercle. Les soldats romains tuent le 1er soldat, puis tuent un soldat sur k jusqu'à ce qu'il n'y ait plus que s survivants. On demande le(s) numéro(s) du(des) survivants.
Résoudre ce problème en utilisant une liste chainée.
def josephe(n, k, s):
"""
Résoud le problème de Josèphe. Les soldats sont numérotés de 1 à n
@param n : entier >= 1, nombre initial de soldats
@param k : entier >= 2, saut entre deux meurtres de soldats
@param s: entier >=0, nombre de soldats survivants
@return survivor : liste d'entiers, numéros des sopldats survivants
"""
survivor = CelluleL()
return survivor
#tests à compléter (ça ne risque pas de fonctionner avec les "?")
print("un soldat sur deux")
for i in range(1, 42):
print("Survivant pour ", i, "soldats :",josephe(i,2,1).???)
print()
tset = josephe(41, 3, 2)
print("2 survivants pour 41 soldats, avec 1 sur 3 :", tset.????, tset.????)
tset = josephe(1234,7, 10)
print("10 survivants pour 1234 soldats, avec 1 sur 7 :", tset)
Un deuxième type de liste : la liste chaînée circulaire¶
Une liste chaînée circulaire est une liste chaînée dans laquelle le dernier élément n'est pas la liste vide, mais le premier élément de la liste. les listes chaînées circulaires sont notamment utilisées pour représenter des files. Cette structure de données est particulièrement adaptée à la résolution du problème de Josèphe. Mais elle est aussi utilisée par exemple pour gérer le partage du processeur (CPU) entre différents programmes (différents processus).
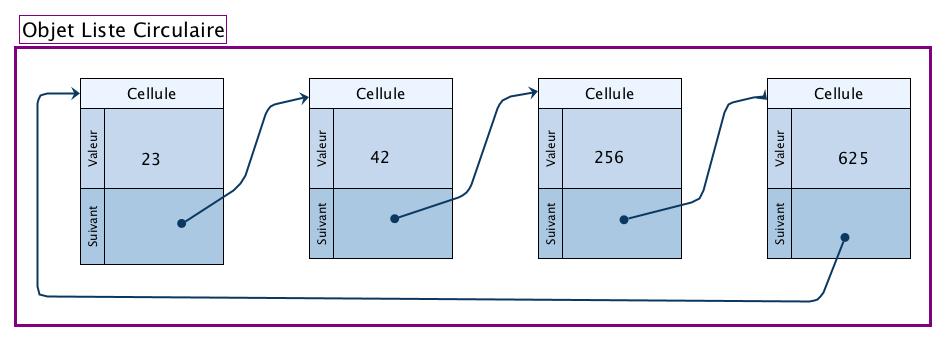
On peut proposer différentes interfaces pour ce type de données. Dans le cadre de ce TP, les primitives proposées de ListeCirc sont :
- Test de vacuité d'une liste :
estVide(liste) - Obtention de la longueur de la liste :
longueur(liste) - Ajout d'un élément en fin de liste :
ajoutfin(donnee) - Supprimer la cellule courante connaissant la précédente:
supprimer(courant , precedent)
Une implantation de cette structure est proposée ci-dessous. Elle possède deux classes, Noeud et ListeCirc. La classe Noeud est celle de la liste chaînée non circulaire, l'attribut longueuren moins.
Les attributs de Noeud sont:
donnée: le contenu du noeudsuivant: le noeud suivant
La classe ListeCirc comporte deux noeuds : tête et queue. Plus précisément, les attributs à la création sont :
tête:Noeud(None par défaut, ou données de la tête)queue: égale àtêtelors de la création de la liste circulairetête.suivant:queue. Le noeud suivant la tête est la queuequeue.suivant:tête. Le noeud suivant la queue est la tête
Remarques / questions :
- On aurait pu proposer une implémentation sans objet
ListeCirc, et de même on aurait pu proposer un objetListeChainee, qui aurait contenu les cellules de la liste chaînée non circulaire. On voit que les possibilités d'implémentations sont multiples. - Utiliser les mêmes noms de primitives permet d'écrire des programmes fonctionnant de manière identique avec les deux structures de données. Ce qui peut être très pratique.
- La liste vide est composée d'une seule cellule, de donnée
None, pointant sur elle-même. Lors du calcul de la longueur, de l'insertion ou de la suppression d'un élément, on est obligé de différencier ce cas. Le code est plus complexe que pour la liste chaînée non circulaire. - Pourquoi utilise-t-on ici deux classes, Noeud et ListeCirc ?
- Pourquoi ne reprend-on pas directement le calcul de la longueur comme dans le cas de la liste chaînée ?
class Noeud:
def __init__(self, donnee, suivant = None):
self.donnee = donnee
self.suivant = suivant
def __repr__(self):
if self.donnee == None:
return ""
else:
return str(self.donnee)
class ListeCirc:
def __init__(self, donnee_tete = None):
self.tete = Noeud(donnee_tete)
self.queue = self.tete
self.tete.suivant = self.queue
self.queue.suivant = self.tete
def estVide(self):
return self.tete.donnee is None
def longueur(self):
lg = None
return lg
def supprimerCourant(self, precedent, courant):
# Suppression du noeud courant connaissant le précédent
if self.tete == self.queue : # cas particulier : un seul noeud
self.tete.donnee = None
elif courant == self.tete : # cas particulier : suppression de la tête
self.tete = self.tete.suivant
self.queue.suivant = self.tete
elif courant == self.queue : # cas particulier : suppression de la queue
self.queue = precedent
self.queue.suivant = self.tete
else: # cas général
precedent.suivant = courant.suivant
def ajoutfin(self, donnee):
if self.tete.donnee is None: # on remplit d'abord la tête
self.tete.donnee = donnee
else: # sinon on crée un nouveau noeud
nouveauNoeud = Noeud(donnee)
self.queue.suivant = nouveauNoeud # On ajoute le noeud à la fin
self.queue = nouveauNoeud # il devient la nouvelle queue
self.queue.suivant = self.tete # et pointe sur la tête
def __repr__(self):
if self.tete.donnee is None :
return 'Liste vide'
else:
chaine = str(self.tete.donnee) + "->"
courant = self.tete
while courant.suivant != self.tete and courant.suivant.donnee is not None :
courant = courant.suivant
chaine = chaine + str(courant.donnee) + "->"
chaine = chaine + "tête"
return chaine
Jeu de tests¶
Comme pour la liste chaînée, créer un jeu de tests pour les méthodes de la liste chaînée circulaire.
Attention ici pas d'indices. Faire notamment un test pour supprimer la tête d'une liste, et pour supprimer le 2ème ou 3ème élément d'une liste.
Le retour de Flavius¶
Résoudre le problème de Flavius Josèphe avec une liste chaînée circulaire.
Remarque : on utilisera la spécificité des listes circulaires, un petit schéma pour s'en sortir sur les courants/précédents est bien utile
def josephe(n, k, s):
"""
Résoud le problème de Josèphe. Les soldats sont numérotés de 1 à n
@param n : entier >= 1, nombre initial de soldats
@param k : entier >= 2, saut entre deux meurtres de soldats
@param s: entier >=0, nombre de soldats survivants
@return survivor : liste d'entiers, numéros des sopldats survivants
"""
survivor = ListeCirc()
return survivor
print("un soldat sur deux")
for i in range(1,42):
print("Survivant pour ", i, "soldats :",josephe(i,2,1).tete.donnee)
print()
tset = josephe(41,3,2)
print("2 survivants pour 41 soldats, avec 1 sur 3 :", tset.tete.donnee, tset.queue.donnee)
tset = josephe(1234,7,10)
print("10 survivants pour 1234 soldats, avec 1 sur 7 :", tset)
S'il vous reste du temps¶
- Construire un jeu de tests aussi complet que possible pour la classe
ListeCirc. - Coder la méthode
longueurpour la classeListeCirc. - Coder des méthodes
lire(liste , k),supprimer(liste , k)etinserer(liste , k)pour la classeListeCirc. - Le fin du fin serait d'avoir la même interface pour les deux classes
listeCiretlisteChainee(mêmes méthodes avec les mêmes spécifications), afin de pouvoir les utiliser indifféremment. L'optique de ce TP était de montrer deux types d'implémentation différents. Mais si vous en avez le courage, vous pouvez écrire la classelisteChainee, y mettre toutes les méthodes auparavant dansCelluleL, et compléter les deux classes afin que leur interface soit identique.

Ce(tte) œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.
frederic.mandon@ac-montpellier.fr, Lycée Jean Jaurès - Saint Clément de Rivière - France (2015-2019)