Remarque préliminaire : Jupyter est parfois capricieux pour le téléchargement des images. Si les images n'apparaissent pas dans le notebook, chargez les dans le même dossier que le notebook. Les adresses se trouvent en double cliquant dans les cellules de texte (là où il y a précisé "image", c'est qu'il y a une image normalement...). Puis changez le code comme ceci :  devient  ou même 
Structures de données linéaires¶
Les structures de données linéaires sont des suites d'éléments $e_1 , e_2 , \dots , e_n$. Dans une structure linéaire, on traite les données séquentiellement, c'est-à-dire les unes après les autres. De plus on doit pouvoir ajouter et supprimer des éléments.
On va s'intéresser à trois types de structures linéaires : les listes, les piles et les files.
Compléter ce cours/TD au fur et à mesure que vous le faites. Pour écrire dans une cellule, double-cliquez dedans. Une fois le TD fait, imprimez-le : pour réviser, la mémorisation se fait mieux avec un cours papier que sur écran.
Les listes¶
Une première remarque fondamentale : on ne parle pas du type listvu en Python en première. Le type listde Python est en fait un tableau dynamique.
Une liste en informatique est une suite d'éléments. Cette suite est finie, et peut être vide. Chaque élément de la suite est repérée par son indice : la liste est ordonnée par l'indice (et non par la valeur de l'élément).
Deuxième remarque : une liste informatique n'est pas non plus ce qu'on appelle une liste dans le langage courant. Quand on a une liste de courses, on ne suit pas l'ordre de la liste pour faire ses courses. Et on ne met pas deux fois le même ingrédient (sauf étourderie). Dans un style plus littéraire, vous pouvez lire les notes de chevet (枕草子, Makura no sōshi) de Sei Shōnagon, écrites vers 990. Ce sont des listes poétiques : "Choses dont on néglige souvent la fin", "Choses que l'on méprise", "Choses qui font battre le cœur", "Fleurs des arbres", "Cascades"...
Une liste est généralement définie comme une liste chaînée, avec un élément de tête, avec ensuite une autre liste, qui contient les éléments suivants. On a ici une définition récursive de la structure de données liste. Chaque élément de la liste est une cellule ou un maillon (cell).
Exemple à compléter :
On donne la liste L1des jours de la semaine :
L1 = [lundi , mardi, mercredi , jeudi , vendredi , samedi , dimanche]
L1a pour tête ... à compléter ... et est suivie de la liste L2 =... à compléter...
L2a pour tête ... à compléter ... et est suivie de la liste L3 = ... à compléter ...
Donner la dernière étape de cette décomposition:
Appeler le professeur pour vérification
Une défintion simple du type Liste utilise les primitives (c'est-à-dire les méthodes de la classe) suivantes :
- construction d'une liste vide :
creerListe() - test de vacuité d'une liste :
estVide(liste) - Ajouter un élément en tête de la liste :
cons(élément). C'est en fait le constructeur "historique" du typeliste. - Renvoyer le premier élément de la liste sans le supprimer :
car(liste). Renvoie la "tête" de liste - Renvoyer la liste, éventuellement vide, obtenue à partir de la liste initiale en supprimant son premier élément. :
cdr(liste , k). Renvoie la "queue" de la liste.
Une liste L peut s'écrire L = cons(car(L) , cdr(L)). On remarque que cette définition est récursive ; cdr(L)pouvant être une liste.
Une implémentation est donnée ci-dessous, basée sur des cellules (tête , queue). Construire des fonctions ou des méthodes permettant de renvoyer un tableau dynamique Python (type list, entre []) et de donner la longueur de la liste (sans passer par le tableau dynamique de Python).
Exercices (sur papier ou à compléter dans la cellule) :¶
On utilisera uniquement les fonctions primitives définies ci-dessus
- Créer la liste de vos quatre films préférés. les films doivent être dans l'ordre de vos préférences. Essayez d'écrire une seule ligne.
- On donne une liste L1. Ecrire un algorithme en langage naturel renvoyant la liste L2, qui est dans l'ordre inverse de L1.
Une première implémentation¶
Compléter le code suivant pour implémenter toutes les primitives du type liste. L'unique attribut de cette classe est :
cellule: la liste proprement dite Les attributs de la classeCellsont :tete: l'élément de tête de la liste (éventuellementNone)queue: la liste composant la deuxième partie deCell(éventuellementNone)
Compléter le code en rajoutant les primitives longueurListe qui, comme son nom l'indique, renvoie la longueur de la liste ; et listeElements, qui, comme son nom l'indique moins clairement, renvoie un tableau dynamique Python (type 'list) comportant les éléments de la liste.
class Cellule :
def __init__(self, tete, queue) :
self.car = tete
self.cdr = queue
class Liste :
def __init__(self, c) :
self.cellule = c
def estVide(self):
return self.cellule is None
def car(self):
assert not(self.cellule is None) , 'Listevide'
return self.cellule.car
def cdr(self):
assert not(self.cellule is None) , 'Listevide'
return self.cellule.cdr
def __repr__(self):
if self.estVide() :
return '()'
else:
return '(' + repr(self.car( )) + ',' + repr(self.cdr()) + ')'
def longueurListe(self):
return
def listeElements(self) :
return
def cons(tete, queue) :
return Liste(Cellule(tete, queue))
nil = Liste(None) # notation "nil" historique
print("liste nil : ",print(nil)," de longueur : ",nil.longueurListe(),". Test pour vide :",nil.estVide())
#print("la liste nil a pour tête ", nil.car() , " et pour queue ",nil.cdr())
liste = Liste(Cellule(4,nil))
for i in range(3,-1,-1):
liste = Liste(Cellule(i,liste))
print("liste :" , liste," de tête ",liste.car()," et de queue ",liste.cdr())
print("Qu'est-ce ? : " , liste.cdr().cdr().car())
print("la longueur de la liste est : ",liste.longueurListe())
"""
print("Conversion en tableau dynamique :", liste.listeElements())
print ("3 est dans ",liste," : ",liste.appartient(3))
print ("7 est dans ",liste," : ",liste.appartient(7))
# Egalité de listes
listeb = Liste(Cellule(4,nil))
for i in range(3,-1,-1):
listeb = Liste(Cellule(i,listeb))
print(listeb , "est égale à ",liste," : ", liste.estEgale(listeb))
listeb = cons(4,listeb)
print(listeb , "est égale à ",liste," : ", liste.estEgale(listeb))
"""
print()
Tester votre code avec les réponses aux exercices précédents. Pour l'exercice 1, on rédigera le test sous forme d'un assert(). Pour l'exercice 2, on pourra rajouter une méthode inverser(liste).
Exercices¶
- Donner la complexité dans le pire des cas des méthodes
estVide(),longueur(),listeElements() - Ecrire une méthode
estEgale(liste2)qui teste si la liste2 est égale à la liste appelant la méthode. - Ecrire une méthode
appartient(element)qui renvoieNonesi l'élément n'appartient pas à la liste, et son indice sinon. Complément pour ceux qui vont vite : en déduire une méthodesupprElement(element)qui supprime la première occurence d'un élément donné dans une liste - Pour ceux qui vont vite. Ecrire une méthode
derniere(liste)qui renvoie la dernière cellule de la liste. En déduire une méthodeconcatener(liste2)qui concatène la liste2 en fin de la liste appelant la méthode.
Autres versions des listes¶
On peut créer d'autres versions des listes:
- Listes basées sur des tableaux. On perd l'intérêt des listes, qui est d'insérer facilement un élément
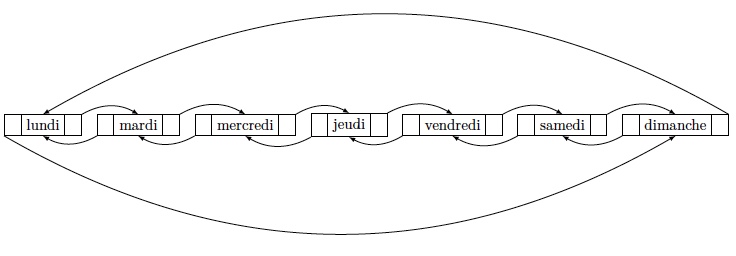
- Listes circulaires. Permet de boucler en fin de liste sur le premier élément
- Listes doublement chaînées. Permet de connaîter non seulement l'élément suivant dans la liste, mais aussi le précédent
- Listes doublement chaînées circulaires
Rappel sur une remarque importante : le type abstrait Listen'est pas le type list de Python. Les listes de Python sont basées sur des tableaux, et mélangent des accès de type fonctions (del(ma_liste[3]), des accès de type objet (ma_liste.append('truc')), et des accès plus étranges (machin in ma_liste , ma_liste[3:6])
Une deuxième implémentation¶
Changer la programmation des méthodes longueurListe() et listeElements() (vous pouvez par exemple passer de l'itératif au récursif, et vice-versa).
Le changement de programmation change-t-il l'usage de la classe ?
Réponse : l'implémentation de la classe ne change pas sa signature, c'est-à-dire que l'usage pour l'utilisateur ne change pas
Types abstraits¶
Comme vous venez de le voir juste ci-dessus, la manière dont est programmée la classe n'influe pas sur son usage. Plus précisément, l'implémentation de la classe ne joue pas sur sa signature. Le type de données Liste peut être définit de manière abstraite. Par exemple, pour utiliser des flottants en Python, vous n'av(i)ez pas besoin de connaître la représentation sous la forme mantisse-exposant, forme que l'on a vue dans le cours sur le codage.
On définit un type abstrait par sa signature : nom des opérations, type des arguments, type du retour des opérations.
Autant l'implémentation d'un type abstrait ne joue pas sur sa signature, par définition même, autant elle peut jouer sur la complexité des opérations du type.
Des primitives différentes pour le type liste¶
Le type Liste n'est pas fixé dans le marbre. On peut proposer des primitives plus nombreuses et plus riches.
On propose ici les fonctions primitives sur les listes suivantes :
- construction d'une liste. La liste peut être vide, ou bien on peut la construire à partir d'un élément de tête et d'une autre liste. On appelle cette fonction :
creerListe(e = Aucun , liste = Aucun) - test de vacuité d'une liste :
estVide(liste) - Obtention de la longueur de la liste :
longueur(liste) - Accéder au k-ième élément de la liste :
lire(liste , k) - Supprimer le k-ième élément de la liste :
supprimer(liste , k). Cette méthode renvoie une nouvelle liste. - Insérer un élément en k-ième position dans la liste :
inserer(liste , k). Cette méthode renvoie une nouvelle liste.
Exercice pour ceux qui vont vite : programmer les méthodes insérer et supprimer, dans l'implémentation suivante du type liste. On peut éventuellement refuser l'insertiion d'un élément en dernière position (c'est un cas particulier à traiter)
class Cell:
def __init__(self , tete = None , queue = None):
self.car = tete
self.cdr = queue
def __repr__(self):
if self.car is None :
return '()'
else:
return str(self.car) + "-" + str(self.cdr)
class Liste :
def __init__(self, *args):
#if isinstance(queue, Liste):
#print(queue," est une liste")
if len(args) == 0:
# No parameter: builds an empty list
self.cell = None
elif len(args) == 2:
# Two parameters: an element and a list
if isinstance(args[1], Liste):
self.cell = Cell(args[0], args[1])
else:
print("le deuxième argument du constructeur doit être une liste")
else:
print("le constructeur de liste prend au plus 2 arguments")
def estVide(self) :
return self.cell is None
def longueur(self) :
long = 0
while not self.estVide():
long = long + 1
self = self.getQueue()
return long
def lire(self , i) :
if i >= self.longueur() :
raise IndexError('Index trop grand')
else :
while i > 0:
i = i - 1
self = self.getQueue()
return self.getTete()
def supprimer(self , i) :
return
def inserer(self , i, element) :
# peut éventuellement insérer en fin de liste avec i = self.longueur()
return
def getTete(self) :
if not self.estVide() :
return self.cell.car
def getQueue(self) :
if not self.estVide() :
return self.cell.cdr
def __repr__(self) :
if self.estVide() :
return '()'
else:
return '(' + repr(self.getTete()) + ',' + repr(self.getQueue()) + ')'
truc = Liste()
print(truc, truc.estVide())
maliste = Liste("film5",truc)
for i in range(4 , -1 , -1) :
maliste = Liste("film"+str(i),maliste)
print("affichage : ",maliste, "de longueur ",maliste.longueur())
print("lecture des éléments d'indices 1 et 5 :",maliste.lire(1),maliste.lire(5))
print()
i = 5
print("Suppression puis ajout de l'élément d'indice ",i, " en itératif")
maliste = maliste.supprimer(i)
print("affichage : ",maliste, "de longueur ",maliste.longueur())
maliste = maliste.inserer(i , "film5b")
print("affichage : ",maliste, "de longueur ",maliste.longueur())
print()
i = 3
print("Suppression puis ajout de l'élément d'indice ",i, " en récursif")
maliste = maliste.supprimerRec(i)
print("affichage : ",maliste, "de longueur ",maliste.longueur())
maliste = maliste.insererRec(i , "film3b")
print("affichage : ",maliste, "de longueur ",maliste.longueur())
Piles¶
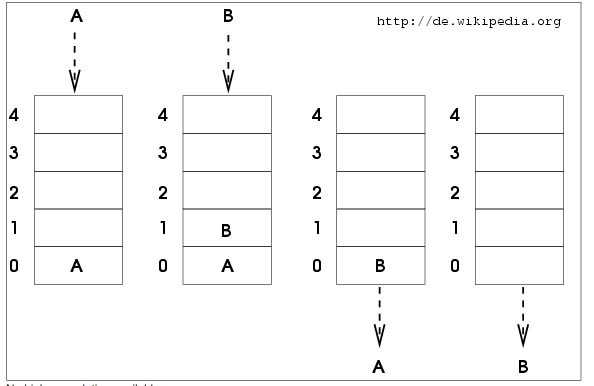
Une pile est une structure linéaire où les insertions et les suppressions se font toutes du même côté, à l'image d'une pile d'assiettes : on rajoute les nouvelles assiettes au sommet de la plie, on prend des assiettes sur le sommet de la pile également. Les piles sont appelées stack ou LIFO en anglais (last in, first out).
Une interface (un peu plus détaillée que la signature) d'une pile peut être :
| Fonction (créerPile)/méthode(les autres) | Description |
|---|---|
| creerPile() $\rightarrow$ Pile | Créer une pile vide |
| estPileVide(p) $\rightarrow$ Booléen | Teste si la pile p est vide |
| empliler(p , élément) | Insère élément en tête de p |
| depiler(p) $\rightarrow$ élément | Enlève l'élément au sommet de la pile p et le renvoie |
| sommet(p) $\rightarrow$ élément | Renvoie l'élément au sommet de la pile p |
Exercices Piles 1¶
- Dans quel état se trouve une pile vide après les opérations suivantes
- empiler(1)
- empiler(2)
- dépiler
- empiler(3)
- empiler(4)
- empiler(5)
- dépiler
- dépiler
- Créer le type
Pile, le tester. Si vous avez implémenté ce type d'une manière différente de votre voisin, vous pouvez tester et comparer l'efficacité de vos implémentations avec%timeit (mon_test(...))
from random import randint
class Pile :
def __init__(self) :
def estPileVide(self):
return
def empiler(self , element):
def depiler(self):
if self.estPileVide():
raise IndexError("la pile est déjà vide")
else :
def __repr__(self):
if self.estPileVide() :
return 'Pile vide'
else:
return
def creerPile():
return Pile()
# un test parmi d'autres
a = creerPile()
for i in range(6):
a.empiler(randint(1, 20))
print(a)
print(a)
for i in range(6):
a.depiler()
print(a)
il est légitime de se demander à quoi sert une pile en informatique. On en trouve dans la gestion des modifications de documents dans les traitements de texte. Dans LibreOffice, ctrl-z permet d'annuler la dernière modification du texte, en "dépilant". On peut itérer cette opération. De même dans les navigateurs, le bouton "page précédente" cache une pile conservant les adresses visitées.
Plus généralement, on a précédemment mentionné les "piles d'appel", notamment en programmation récursive. C'est bien une structure du type abstrait pile qui est utilisée.
Exercice Piles 2¶
3 . Ecrire une deuxième implémentation de la structure Pile. Si vous ne l'avez pas fait, utilisez la classe précédente Cellule pour cela : on peut réaliser Pile très économiquement à partir de cette dernière. C'est le code proposé ci-dessous, il ne reste que depilerà coder. Et si vous avez déjà utilisé Cellule, implémentez par exemple à partir de tableaux (type list) Python.
class Cellule :
# On reprend la définition de la cellule d'une liste chaînée
def __init__(self, haut, suite) :
self.haut = haut
self.suite = suite
def __repr__(self):
if self.haut is None :
return 'cellule vide'
elif self.suite is None :
return str(self.haut)
else :
return str(self.haut) + "-" + str(self.suite)
class Pile :
def __init__(self) :
self.pile = None
def estPileVide(self):
return self.pile is None
def empiler(self , element):
self.pile = Cellule(element , self.pile)
def depiler(self):
def __repr__(self):
if self.estPileVide() :
return 'Pile vide'
elif self.pile.suite is None:
return repr(self.pile.haut)
else :
return repr(self.pile.haut) + '-' + repr(self.pile.suite)
def creerPile():
return Pile()
ma_poule = creerPile()
print(ma_poule)
ma_poule.empiler(1)
print(ma_poule)
ma_poule.empiler(2)
print(ma_poule)
ma_poule.depiler()
print(ma_poule)
ma_poule.empiler(3)
print(ma_poule)
ma_poule.empiler(4)
print(ma_poule)
ma_poule.empiler(5)
print(ma_poule)
ma_poule.depiler()
print(ma_poule)
ma_poule.depiler()
print(ma_poule)
Encore un exercice (plus amusant)¶
La notation polonaise inverse (notation postfixe) est une manière de noter les calculs sans utiliser de parenthèses. Cette notation a été utilisée ar certaines calculatrices, notamment de Hewlett-Packard.
Exemple : calcul de 7 8 * 2 +
- On lit les deux premiers nombres et l'opérateur, on calcule 7*8 = 56
- On garde le 56 en tête, on lit le nombre et l'opérateur suivant : 56 + 2 = 58 qui est le résultat du calcul
Pour cet exercice, on n'utilisera que des nombre positifs et pas de division (pour éviter la division par 0) . L'évaluation d'une expression est simple et utilise une pile :
- Initialement la pile est vide
- Si on trouve un nombre, on l'empile
- Si on trouve un opérateur, on dépile deux fois pour trouver les deux opérandes (attention à l'ordre pour la soustraction, non symétrique). On effectue l'opération, et on empile le résultat
- Le résultat de l'opération se lit en sommet de pile.
- Sur papier, donner le résultat de 1 2 3 4 + x 5 x - 7 + . Ecrire ce calcul sous forme infixe (c'est-à-dire de la manière usuelle avec les parenthèses).
- Ecrire une fonction Python qui, étant donnée une chaîne de caractères exprimant un calcul sous forme postfixe, donne le résultat du calcul, sous les préconditions : nombres positifs, pas de division, expression "bien formée". La tester.
Rappel : la méthode
splitpermet d'obtenir une liste comportant les différents "mots" d'une chaîne de caractères. Utilisée sans arguments, le séparatuer est l'espace :'un deux trois'.split()renvoie['un', 'deux', 'trois'].
def calculPostFixe(calcul) :
pile = Pile()
return
print(calculPostFixe("1 2 3 4 + * 5 * - 7 +"))
Files¶
Une file est une structure linéaire où les insertions et les suppressions se font à l'opposé l'une de l'autre, à l'image d'une file d'attente : le premier arrivé est le premier servi. Les piles sont appelées FIFO ou queue en anglais (first in, first out).
Une interface possible d'une file est :
| Fonction | Description |
|---|---|
| creerFile() $\rightarrow$ Pile | Créer une file vide |
| estFileVide(f) $\rightarrow$ Booléen | Teste si la file f est vide |
| enfiler(f , élément) | Insère élément en queue de f |
| defiler(f) $\rightarrow$ élément | Enlève l'élément aen tête de la file f et le renvoie |
| tete(f) $\rightarrow$ élément | Renvoie l'élément en tête de la file f |
Exercices Files 1¶
- Dans quel état se trouve une pile vide après les opérations suivantes
- enfiler(1)
- enfiler(2)
- défiler
- enfiler(3)
- enfiler(4)
- enfiler(5)
- défiler
- défiler
Comparer avec l'exercice correspondant sur les piles
- Créer le type
File, le tester. Si vous avez implémenté ce type d'une manière différente de votre voisin, vous pouvez tester et comparer l'efficacité de vos implémentations avec%timeit (mon_test(...))
from random import randint
class File :
# Implémentation avec un inconvénient majeur : defiler(self) est lent, car autant liste.pop()
#est en temps constant, autant liste.pop(0) est en temps linéaire
def __init__(self) :
def estFileVide(self):
return
def enfiler(self , element):
def defiler(self):
if self.estFileVide():
raise IndexError("la pile est déjà vide")
else :
return
def __repr__(self):
if self.estFileVide() :
return 'File vide'
else:
return
def creerFile():
return File()
# un test parmi d'autres
a = creerFile()
for i in range(6):
a.enfiler(randint(1, 20))
print(a)
print(a)
for i in range(6):
a.defiler()
print(a)
Exercices Files suite¶
3 . Ecrire un programme qui permet de retourner une pile, en utilisant uniquement une file.
def retournerPile(mapile):
return mapile
a = creerPile()
for i in range(6):
a.empiler(i)
print(a)
print(retournerPile(a))
Exercice Files suite (et +/- fin)¶
Implémenter une structure de file à l'aide de deux piles. Pour cela, une des piles est l'entrée, l'autre la sortie. Les deux sont liées. Lorsque l'on ajoute un élément, on l'empile sur l'entrée. Lorsque l'on retire un élément, si la pile de sortie n'est pas vide alors on la dépile (forcément le premier élément). Si la pile de sortie est vide, alors on retourne la pile d'entrée en la mettant sur la pile de sortie (on transforme au passage un structure LIFO en FIFO, puisqu'on inverse la pile d'entrée). Remarquons au passage que la file est vide si et seulement si les deux piles sont vides.
class Pile :
def __init__(self) :
self.pile = []
def estPileVide(self):
return self.pile == []
def empiler(self , element):
self.pile.append(element)
def depiler(self):
if self.estPileVide():
raise IndexError("la pile est déjà vide")
else :
return self.pile.pop()
def __repr__(self):
if self.estPileVide() :
return 'Pile vide'
else:
return str(self.pile)
def creerPile():
return Pile()
class File:
def __init__(self):
self.entree = creerPile()
self.sortie = creerPile()
def estFileVide(self):
return
def enfiler(self , element):
def defiler(self):
def __repr__(self):
if self.estFileVide() :
return 'File vide'
else:
return repr(self.entree) + " - " + repr(self.sortie)
def creerFile():
return File()
# un test parmi d'autres
a = creerFile()
for i in range(4):
a.enfiler(randint(1, 20))
print(a)
for i in range(2):
print("défiler : ",a.defiler())
print(a)
for i in range(4):
a.enfiler(randint(1,20))
print(a)
while not (a.estFileVide()):
print("défiler : ",a.defiler())
print(a)
On constate avec cette implémentation, très différente a priori de ce que vous avez fait précédemment, que le type abstrait Filepeut être traduit en code de manières très différentes les unes de autres.
Le module deque¶
Le type deque(double ended queue, se lit deck) permet l'implémentation directe d'une file, où les primitives enfileret defiler sont en complexité temporelle constante $O(1)$. On donne ci-dessous une exemple de code permettant la création d'une file. Ce type fait partie de la bibliothèque collections.
Exercice : reprendre la fonction qui permet d'inverser une pile avec une file, et la réécrire en utilisant deque (et éventuellement une pile formée tout simplement à partir d'un tableau dynamique Python, type list).
from collections import deque
file = deque()
for i in range(6):
file.append(randint(1, 20))
print(file)
for i in range(6):
file.popleft()
print(file)
# Retourner une pile
def retournerPile(pile):
file=deque()
return pile
poil = []
for i in range(6):
poil.append(i)
print(poil)
print(retournerPile(poil))
Exercices complémentaires¶
Dans ces exercices, la structure de données à utiliser parmi liste, pile et file n'est pas précisée : c'est à vous de la déterminer.
- Bon parenthésage. On donne une chaîne de caractères dans laquelle figurent des parenthèes ouvrantes
(, fermantes), et de même pour les crochets[et]. Ecrire une fonction qui vérifie le bon parenthésage de l'expression.([()])est bien parenthésée,([()]et([(]))ne le sont pas (il manque une)dans le premier cas, et dans le deuxième)et]sont inversés) - Problème de Flavius Josèphe. Flavius Josèphe est un historiographe romain juif du 1er siècle, dont l'oeuvre historique est sujette à caution. Il a donné la première version du problème suivant : "41 soldats juifs, cernés par des soldats romains, décident de former un cercle. Un premier soldat est choisi au hasard et est exécuté, le troisième à partir de sa gauche (ou droite) est ensuite exécuté. Tant qu'il y a des soldats, la sélection continue. Le but est de trouver à quel endroit doit se tenir un soldat pour être le dernier. Josèphe, peu enthousiaste à l'idée de mourir, parvint à trouver l'endroit où se tenir. Quel est-il ?"
Variante : 42 soldats juifs, deux survivants, et les romains en tuent un sur trois.
Sources :
- cours de Clémentine Nebut, Université de Montpellier II
- Wikipedia
- Types de Données et Algorithmes, C. Froidevaux, MC Gaudel, M Soria
- Eléments d'Algorithmique, D. Beauquier, J. Berstel, Ph. Chrétienne
- Document d'accompagnement éduscol Terminale NSI