Lisibilité des programmes¶
Les bibliothèques¶
Une bibliothèque est un ensemble de fonctions préprogrammées, que l'on incorpore en début de programme.
On utilisera principalement les bibliothèques mathématiques (math) et aléatoire (random).
Avant d'utiliser une bibliothèque, autre que les deux précédentes, posez-vous les questions suivantes:
- en ai-je besoin ? (9 fois sur 10 la réponse est non);
- cela va-t-il me simplifier le travail ? (la réponse est souvent non, ça sera bien plus compliqué, mais parfois oui, ça sera beaucoup plus simple...);
- la bibliothèque est-elle dépréciée ? (c'est à dire "périmée mais quand même vaguement comestible à vos risques et périls").
Jusqu'à ce que vous ayez entamé vos projets, vous perdrez du temps à chercher des solutions toutes faites sur le web, et vous apprenez moins bien : je vous déconseille fortement d'utiliser le web comme autre chose qu'une source de documentation. Il est vrai que ça rassure et que ça semble plus simple de chercher sur internet, mais au début c'est une perte de temps pour ce qui est de la programmation proprement dite.
import math
print(math.pi)
print(math.cos(math.pi))
print(math.sqrt(3)) # fonction racine carré (square root = sqrt)
Il y a plusieurs manières d'importer une bibliothèque. Comparez la cellule précédente import math, où l'on précise les fonctions ou variables de la bibliothèque (comme math.pi), avec les trois cellules suivantes from random import random, from random import *, et enfin import random as rd.
C'est la dernière solution qui est privilégiée (import random as rd). Voyez cela comme lorsque l'on cite un auteur : on donne la phrase (ici par exemple la fonction random) et l'auteur (ici rd), pas juste la phrase. Et surtout, lorsque l'on a un code (un programme) long, cela permet de savoir d'où viennent les fonctions utilisées.
from random import random
for i in range(10):
print(random())
from random import *
for i in range(10):
print(randint(3,8))
import random as rd
for i in range(10):
print(rd.randrange(3,8))
for i in range(10):
print(rd.randrange(3,8,2))
Remarques :
- lorsqu'une bibliothèque a été importée, on n'a pas besoin de la réimporter (deux dernières boucles);
- différence entre randint et randrange : compléter
Dessiner avec la bibliothèque Turtle¶
Le module Turtle est un outil graphique qui permet de faire des dessins dans une fenêtre.
Tester le code ci-dessous et l'otimiser.
from turtle import *
forward(100)
left(120)
forward(100)
left(120)
forward(100)
left(120)
Une fonction 'triangle'¶
La logique derrière les fonctions en informatique est la même que celle des fonctions en mathématiques. On donne une variable (ou plusieurs, ou aucune), et on récupère un résultat (ou plusieurs, ou aucun). Les variables sont appelées paramètres, et on dit que la fonction renvoie un résultat.
On reprend le programme précédent, mais on souhaite que l'utilisateur choisisse la taille du triangle. On va écrire ce programme à l'aide d'une fonction.
from turtle import *
def triangle(l_cote):
"""
Dessine un triangle de cote donne
@param l_cote : entier strictement positif, donnant la taille du triangle
@return : ne renvoie rien
"""
for i in range(3):
forward(l_cote)
left(120)
return
l_c = int(input("Quelle est la longueur du côté du triangle ? "))
triangle(l_c)
Remarques :
- La fonction est spécifiée, on précise entre les triples guillemets :
- ce qu'elle fait ;
- quels sont ses paramètres d'entrée, avec leur nom, leur type, les conditions supplémentaires éventuelles (dites préconditions), et leur usage. Ici le nom est
cote, le typeentierouint, la préconditionstrictement positif. Préciser la précondition permet d'éviter de la vérifier dans la fonction, cela doit être fait auparavant par l'utilisateur/le programme qui appelle la fonction. - quelles sont les variables retournées, sous la même forme que les paramètres d'entrée.
- On ne donne pas forcément le même nom aux paramètres (dans la définition de la fonction, ici
l_cote), et aux arguments (lors de l'appel de la fonction, icil_c). Cela peut paraître bizarre. Mais en mathématiques on fait la même chose : on définit bien $f$ par $f(x) = 5x + 3$ puis on calcule $f(2)$. On a de même deux "noms" différents : $x$ qui correspond àl_coteet $2$ qui correspond àl_c.
Une fonction 'polygone'¶
On reprend la fonction précédente, en la transformant de manière à tracer n'importe quel polygône régulier, dont le nombre de côtés et la longueur des côtés sont passés en paramètres. La fonction doit renvoyer l'angle entre deux côtés. Compléter le code
from turtle import *
def polygone(l_cote, n_cote):
"""
Dessine un polygone régulier
@param l_cote : entier strictement positif, donnant la taille d'un côté du polygone
@param n_cote : entier supérieur ou égal à 3, donnant le nombre de côtés du polygone
@return angle : flottant strictement positif (compris entre ? et ?),
angle entre deux côtés du polygone
"""
angle = 0 # à modifier !
return angle
l_c = int(input("Quelle est la longueur du côté du triangle ? "))
n_c = int(input("Combien de côtés a le polygone ? "))
a = polygone(l_c, n_c)
print("l'angle entre deux côtés vaut ", a, "degrés.")
Quelques commandes turtle utiles¶
La tortue est positionnée par défaut au centre de la fenêtre, de coordonnées (0, 0). Pour faire des dessins plus variés, on peut utiliser les commandes suivantes :
up()etdown()permettent de lever le crayon, ainsi la tortue peut se déplacer sans dessiner, et respectivement de le baisser.right(angle)tourne à droite d'un angle donné.backward(distance)recule d'une distance donnée en pixels.position()renvoie la la position(x, y)de la tortue.speed(vitesse)fixe la vitesse de la tortue, avec un entier entre 0 et 10. La vitesse normale est 6. Lent = 1, rapide = 10, pas d'animation (obtenir la figure directement) = 0.circle(rayon)trace un cercle de rayon donné. On peut donner un deuxième paramètre pour tracer un arc de cercle d'angle au centre donné. Le centre du cercle est àrayonpixels de la tortue sur la gauche.hideturtle()etshowturtle()cache/montre la tortueclear()efface le dessin et remet la tortue au centre
Ecrire une fonction qui dessine un segment de longueur donnée en pointillés. Les pointillés feront 1/20 de la longueur du segment. Attention à vérifier que le segment a bien la longueur voulue. Spécifier et tester votre fonction.
Penser aux cas problématiques éventuels (longueur < 20 ou longueur non multiple de 20). Suivant votre aisance, ne pas traiter le cas "longueur < 20", qui offre peut d'intérêt. Le traitement du cas "longueur non multiple de 20" est compliqué, intéressant, mais pas obligatoire pour la suite. Modifier éventuellement les spécifications de la fonction pour tenir compte des cas particuliers traités ou non.
from turtle import *
def pointille(l_segment):
return
l_s = int(input("longueur du segment ? "))
pointille(l_s)
hideturtle()
Ecrire deux fonctions qui réalisent les deux premiers schémas suivants, de plus en plus complexes à tracer. Les segments augmentent par 20 pixels entre chaque polygone. Le nombre de polygones à tracer, ainsi que la taille du segment initial, sont passés en paramètres. Ces fonctions appelleront les fonctions précédemment créées. Pour ceux qui font la spécialité mathématique, le troisième dessin est intéressant à faire, il demande d'utiliser la trigonométrie avec la fonction tangente, et des angles en radians. Par contre il n'apporte rien de plus au niveau programmation : c'est un exercice de mathématiques.
On pourra modifier la fonction polygone pour les deux derniers dessins, et pour la dernière utiliser les méthodes goto(x,y) et color(couleur)de turtle. Les couleurs sont des chaines de caratères données en anglais ("red", "blue", etc.)
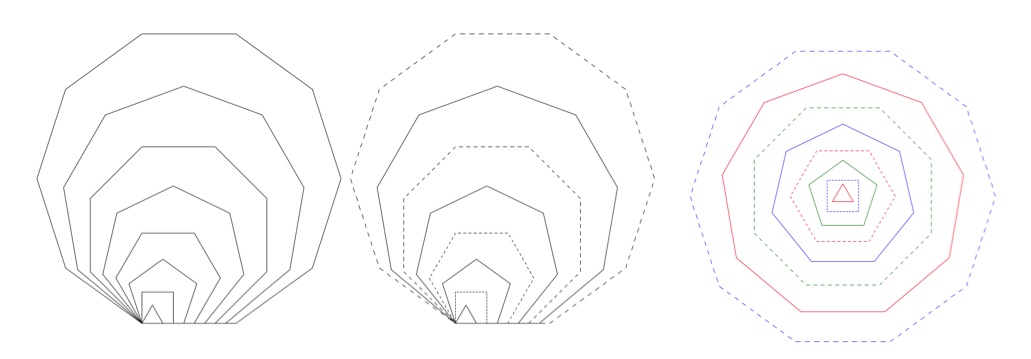
from turtle import *
from math import tan, pi
def polygone(l_cote, n_cote, b_pointilles):
"""
Dessine un polygone régulier
@param l_cote : entier strictement positif, donnant la taille d'un côté du polygone
@param n_cote : entier supérieur ou égal à 3, donnant le nombre de côtés du polygone
@param b_pointilles : booléen vrai si le segment est tracé en pointillés
@return angle : flottant strictement positif (compris entre ? et ?),
angle entre deux côtés du polygone
"""
angle = 0
return angle
De l'intérêt des fonctions¶
Pourquoi programmer en fonctions ?
- parce qu'écrire 10 fois 10 lignes de code indépendantes, c'est plus facile que d'écrire 100 lignes entremélées ;
- parce qu'une fonction bien documentée se réutilise sans se poser de questions : on n'a pas à la retaper, ni à y réfléchir ;
- parce que quand un programme plante, trouver d'où vient l'erreur dans une fonction de 10 lignes est plus facile que dans un code de 100 lignes
- parce que s'il faut modifier/maintenir/corriger le programme, les parties de celui-ci sont clairement identifiées. Les spécifications permettent d'en comprendre l'essentiel ;
- parce que lorsque l'on écrit un programme, la syntaxe "fonction magique" est très pratique : c'est un problème que l'on laisse en suspens pour le moment.
Exemple de fonction magique :
Début
Fonction equation_logarithme(a,b)
fonction magique "résolution d'une équation du type a*ln(x) = b" sans même savoir ce qu'est la fonction logarithme népérien, notée ln
paramètres et retour : on verra ça plus tardrenvoie (1) valeur choisie au hasard
Fin
La traduction en Python :
def eln(a,b):
"""
Resolution de l'equation a.ln(x) = b a faire ulterieuremnt
@param : a ?
@param : b ?
@return : c ?
"""
return (1)
#ci-dessous appel de la fonction dans le print
print("la solution de l'equation 3.ln(x) = 2 vaut",eln(3,2))
# bien sûr le résultat est faux, mais il permet d'avancer dans la programmation
De l'utilité des spécifications¶
Les fonctions ci-dessous ont beaucoup de défauts :
- elles ne sont pas spécifiées, ce qui peut d'ailleurs entrainer des erreurs lors de leur usage ;
- leur nom n'explique pas ce qu'elles font. Par ailleurs il est conseillé d'écrire les noms des fonctions de la même manière que le nom des variables (mots en minuscules séparés par des tirets bas : _ ).
- les noms des variables ne sont pas clairs et/ou cohérents.
Trouver ce que font ces fonctions (en testant c'est plus simple, au moins pour la troisième), les modifier pour les rendre lisibles, et écrire les spécifications.
def xionfonun(grl, jht, klwst):
# ici un exemple de fonction avec deux "return". On peut le faire quand la fonction est très simple
dzaui = (grl + jht + klwst)/3
if dzaui >= 10 :
return True
else :
return False
def ksionfondeux(argh, blu):
zlorg = 0
if blu >= 0 :
while argh >= 0 :
argh = argh - blu
zlorg = zlorg + 1
return zlorg
def malfonction3(hhhjt, hjjjt):
xwtz = 1
while hjjjt != 0 :
if hjjjt % 2 == 1 :
xwtz = xwtz * hhhjt
hjjjt = hjjjt - 1
else :
hhhjt = hhhjt * hhhjt
hjjjt = hjjjt // 2
return xwtz
print(malfonction3(231, 729))
Des erreurs classiques à éviter¶
Les fonctions suivantes montrent quelques erreurs que l'on peut faire en utilisant des fonctions.
On suppose que vous écrivez une lettre au Père Noël et que celui-ci procède à un traitement automatisé des courriers. Expliquez pourquoi les deux premières fonctions présentent une erreur de logique, mais pas la troisième.
def lettre_pere_noel_1(lettre) :
"""
Récupère une lettre écrite au Père Noël. Le dernier mot de la lettre est le cadeau demandé
@param lettre : chaine de caractères
@return cadeau : chaine de caractères
"""
# Erreur à expliquer
lettre = "Cher Père Noël, j'aimerais bien avoir un cerveau"
# on découpe la phrase en mots, et on récupère le dernier mot qui est le cadeau demandé
# ne cherchez pas à comprendre comment ces deux lignes fonctionnent
mots = lettre.split()
cadeau = mots[-1]
return cadeau
def lettre_pere_noel_2(lettre) :
"""
Récupère une lettre écrite au Père Noël. Le dernier mot de la lettre est le cadeau demandé
@param lettre : chaine de caractères
@return cadeau : chaine de caractères
"""
# on découpe la phrase en mots, et on récupère le dernier mot qui est le cadeau demandé
# ne cherchez pas à comprendre comment ces deux lignes fonctionnent
mots = lettre.split()
cadeau = mots[-1]
# Erreur à comprendre
print(cadeau)
def lettre_pere_noel_3(lettre) :
"""
Récupère une lettre écrite au Père Noël. Le dernier mot de la lettre est le cadeau demandé
@param lettre : chaine de caractères
@return cadeau : chaine de caractères
"""
# on découpe la phrase en mots, et on récupère le dernier mot qui est le cadeau demandé
# ne cherchez pas à comprendre comment ces deux lignes fonctionnent
mots = lettre.split()
cadeau = mots[-1]
# Expliquer pourquoi ce n'est pas une erreur
cadeau = cadeau + " chocolats"
return cadeau
print("Erreur 1")
ma_lettre = "Cher Père Noël, j'aimerais bien avoir un vélo"
mon_cadeau = lettre_pere_noel_1(ma_lettre)
print("vous allez recevoir : ")
print(mon_cadeau)
print()
print("Erreur 2")
ma_lettre = "Cher Père Noël, j'aimerais bien avoir un vélo"
mon_cadeau = lettre_pere_noel_2(ma_lettre)
print("vous allez recevoir : ")
print(mon_cadeau)
print()
print("Fonction valable 3")
ma_lettre = "Cher Père Noël, j'aimerais bien avoir un vélo"
mon_cadeau = lettre_pere_noel_3(ma_lettre)
print("vous allez recevoir : ")
print(mon_cadeau)

Ce(tte) œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.
frederic.mandon@ac-montpellier.fr, Lycée Jean Jaurès - Saint Clément de Rivière - France