Lab10 - Introduction to GPS¶
Authors:¶
v1.0 (2014 Fall) Rishi Sharma **, Sahaana Suri **, Paul Rigge **, Kangwook Lee **, Kannan Ramchandran **
v1.1 (2015 Fall) Kabir Chandrasekher *, Max Kanwal *, Kangwook Lee **, Kannan Ramchandran **
v1.2 (2016 Fall) Ashvin Nair ***, Tony Duan ***, David Marn ***, Kabir Chandrasekher **, Kannan Ramchandran *
In this lab, you will learn how GPS signals are used to estimate the location of an object. GPS satellites broadcast several different signals. These signals contain a very accurate measurement of the satellite's time, as well as the satellite's position, velocity, etc.
Overview¶
Part 1.¶
- Finding your location from noisy GPS measurements
- Implementing GPS estimation - first person to get the location and go there gets 1% bonus in the class!
Part 2.¶
- Low-level GPS communication and physics
- Decoding signals with matched filters
Part 1: Finding your location¶
How does a GPS chip determine where it is located?¶
Let's explore what a GPS chip does: we'll build up a simple model, and then let you pretend to be the GPS chip.

We first assume that we have obtained the $N$ GPS signals, each of which gives a noisy measurement of the distance between the GPS satellite and the object.
The noisy measurements are modeled as follows, where $n_i$ is iid Gaussian noise with zero mean and variance $\sigma^2$. $$D_i = d_i + n_i $$
In the above equation, $d_i$ is the actual distance to the $i$-th satellite, and $D_i$ is the reported distance, which is corrupted by additive noise $n_i$. This additive white gaussian noise (AWGN) channel model is actually very common in information theory, and can be analyzed just like how we analyzed the BEC and BSC earlier in the course! It is a pretty good model for satellite communication links as you don't have to deal with shadowing, multipath, excessive interference, etc. (come talk to one of us if you're interested in learning more about this stuff/what it means!)
For simplicity, let's visualize the entire space as a 2D plane. Assume that all GPS satellites and the object to be located (GPS chip) are on the plane. Denote the position of the unknown object as $(x, y)$, and let $(x_i, y_i)$ be the position of the $i$th GPS satellite.
Q1. Find the MLE of $(x, y)$ given $\{(x_i,y_i)\}$ and $\{D_i\}$.¶
Hint 1: To get started thinking about the problem, consider the case where $\sigma=0$, i.e., noiseless distance measures are given. What is the minimum $N$ necessary to estimate the unknown position exactly, and how would you estimate it?
Hint 2: Leave your answer in the form of an expression to be maximized (as in, something proportional to the likelihood function)
Hint 3: Use the distance formula. What is the relationship betweek $d_i$ and $(x_i,y_i)$?
Q1. Answer here¶

Subject: [cory-info] CORY HALL BURGLARY YESTERDAY NIGHT BETWEEN 11:03 P.M.- 11:44 P.M.¶
Date: Wed, April 6, 2016 at 10:19 AM¶
Dear Building Occupants:
Yesterday night between 11:03 p.m. and 11:44 p.m. the BLISS Lab was burglarized. The elapsed time for entry, theft and exit from the building was approximately 6 minutes. To prevent thefts from occurring inside or nearby Cory Hall and Soda Hall please remember to:
- Be AWARE of your surroundings; Be aware;
- Lock up all personal belongings when you leave the building
- Never prop doors open allowing individuals without card key access to enter a secure space
Don’t allow strangers to “tail gate” behind you through card reader controlled doors. Immediately report any suspicious activity to UCPD at (510) 642-6760 and myself at (415) 713-3403.
BE SAFE, REMAIN VIGILIGENT and AWARE.¶
======================================================================================================================
Indeed, the hidden secret of EE126 is stolen from Kangwook’s desk in the BLISS lab. The note has been secretly shared among teaching staffs at Berkeley for more than 50 years, and has been secret sauce of EE126.
Note: Treat all (x,y) coordinates in the following paragraphs as (latitude, longitude).

Fortunately, the UCPD promptly reacted and caught the suspect, but the suspect didn’t possess the note; he claims that he lost it while escaping. We believe that he must have dropped the note at $(x_0, y_0)$, where he started running at a constant velocity $(v_x, v_y)$ for $99$ minutes until he reached $(x_{99}, y_{99}) = (x_0,y_0) + 99(v_x, v_y)$. We found that the GPS sensor in his iPhone has collected distance measurements from $5$ GPS towers in the SF bay area for $99$ minutes. The GPS towers are located as described in the following figure.

The UCPD asked us to locate the treasure (or $(x_0,y_0)$). We need your help! The location of the GPS towers and measurement data are provided below. If you think that you found the location of the secret, please check out the location. Whoever finds the ‘secret notes’ and return the notes without opening it will be awarded 1% bonus to his/her final grade. If you physically find the note, please make a post on Piazza declaring your victory to gloat so other teams know not to go searching.
Thanks,
EE126 teaching staff
Q2. Using the sensor positions and measured distances please locate the treasure.¶
import numpy as np
# (x,y) coordinates of the 5 GPS towers
sensor_position = [(37.7,-122.3), (37.9,-122.15), (37.83,-122.15), (37.91, -122.4), (37.9, -122.21)]
# measured_dist[i, j]: measured distance from tower j at time i
measured_dist = np.load('measured_dist.npy')
n_of_sensors = len(sensor_position)
n_of_timeslots = len(measured_dist)
# Q2. your solution here
Part 2: Data Acquisition¶
GPS receivers make use of the fact that light propagates at a known speed, so the receiver can compute distances from the satellites by measuring how long it takes the GPS signal to propagate from the satellite to the receiver. This requires very accurate time measurements — light in free space travels 300m in a microsecond, so small timing errors result in huge distance errors.
The first section of the lab will be to determine how a GPS chip actually goes about receiving and decoding signals. We will step through a subset of problems that must be combatted to successfully send signals from a satellite to your GPS chip. The second portion of the lab will then explore how a GPS chip can use the data it receives to determine its location, assuming the raw, received signals were acquired and decoded. We end with a little open-ended challenge for you. Hope you have fun!
How does a GPS chip decode received signals?¶
When you a turn a GPS on, it immediately begins to listen for satellite signals. The satellites are continuously transmitting data, and the GPS chip is expected to receive this signal and make sense of it.
The first signal a GPS receiver attempts to find is the Coarse/Acquisition signal. This contains a 1500 bit chunk of data called the "almanac." It contains information and status concerning all the satellites (locations and status) agreed upon by all satellites and is valid for approximately 180 days. This signal is sent at a very low data rate and is intended only to give the receiver a rough idea of the time/location before moving on to the higher data rate, more precise signals. In this lab, we will only focus on the almanac being modulated over the C/A signal.
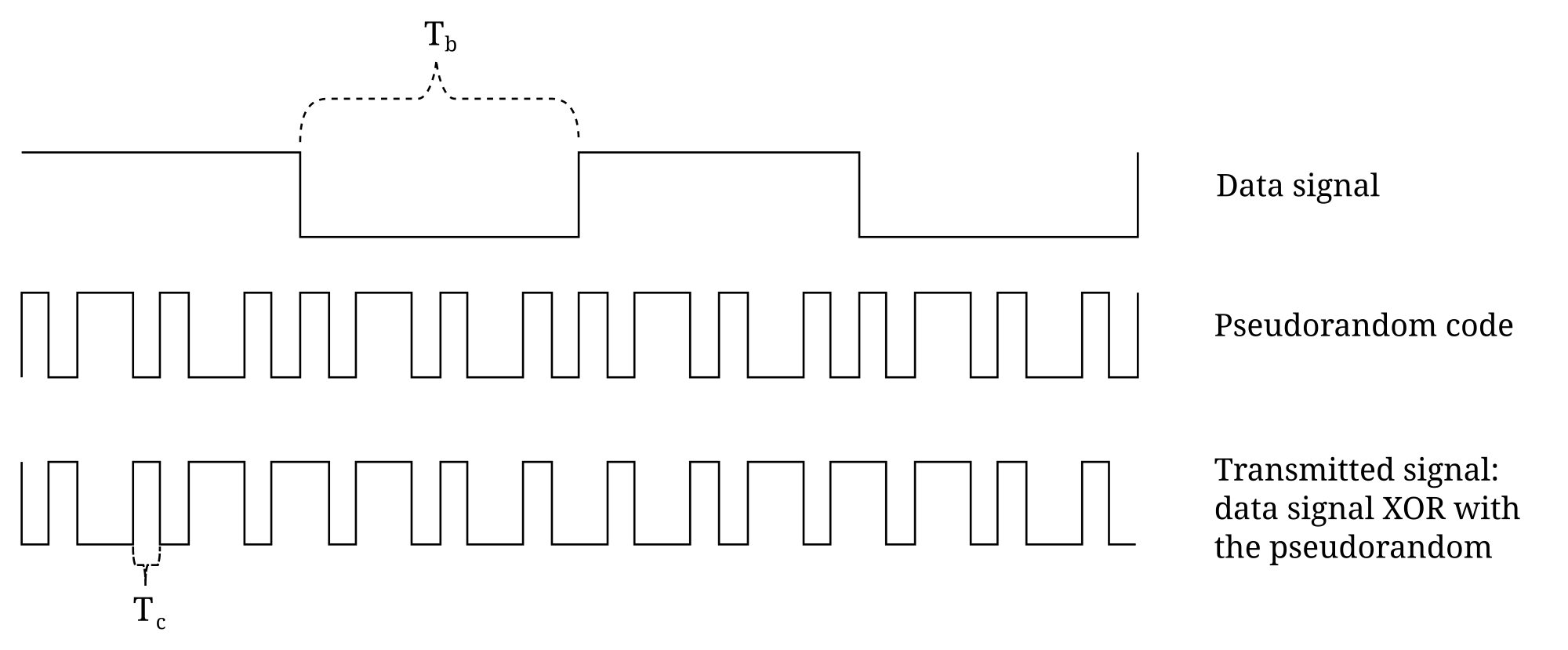
A simplified version of the C/A signal is depicted and described below.
Data bits (data signals) from each satellite is transmitted at 50 bits / second. This slow data signal is xor'd with a much faster pseudorandom bit sequence (pseudorandom noise, PRN) that repeats every millisecond (1023 samples). Each satellite transmits with a unique PRN that will not correlate with any other satellite's code (the codes orthogonal to one another, and will "cancel each other out" when xor'd together). This is a form of "Code Division Multiple Access," (CDMA) where multiple transmitters can send messages over a single channel without risk of collision. As long as each PRN is orthogonal to the rest, each data signal can be independently recovered.
See http://en.wikipedia.org/wiki/GPS_signals, http://en.wikipedia.org/wiki/Code_division_multiple_access#Steps_in_CDMA_modulation, and come talk to us if you're interested in learning more about this!
The following code allows you to simulate an idealized GPS receiver with some plausible parameters.
The pseudorandom code is generated by a linear feedback shift register (see http://en.wikipedia.org/wiki/Linear_feedback_shift_register).
The function transmit_to_earth(signal) simulates what the signal might look like by the time it reaches your receiver. Skim through the code, but don't worry if you don't understand all of it.
import numpy as np
import scipy.signal
# linear feedback shift register, default for taps is that used by GPS C/A Signal
def lfsr(n, starting_state=(1 << 10) - 1, taps=[3,10]):
state = starting_state
for i in range(n):
yield state
state = ((state << 1) & ((1 << max(taps))-1)) + \
reduce(lambda x,y: x^y, map(lambda x: state & (1<<(x-1)) != 0, taps), False)
# coarse/acquisition code generation. reset is all 1's state. This is data that
# is modulated by a pseudorandom bit sequence.
def ca(starting_state=(1 << 10) -1):
return np.fromiter( ( 2*(i >> 9)-1 for i in lfsr(1023, starting_state=starting_state)), dtype=np.float)
ca_canonical=ca()
offset = int(np.random.uniform(0, ca_canonical.size))
# adapted from http://common.globalstar.com/doc/axonn/GPS-L1-Link-Budget.pdf
def transmit_to_earth(signal, temp=290, offset=offset, bw=2e6, SNR_boost=0, NF=0):
signal = np.roll(signal, -offset) # add a random phase
elevation = 2.5e7 #m, approximately over the horizon
antenna_gain = 13. #dBi
power = 46.5 #dBm
c_lambda = .1904 #m
temp = 290 #K
thermal_noise = 10*np.log10(1.38e-23 * temp) + 30 #kT in dBm
# Carrier to Noise ratio in dB
CbyN0 = power + antenna_gain - 20 * np.log10(4*np.pi * elevation / c_lambda) - thermal_noise
SNR = CbyN0 - 10*log10(bw) + SNR_boost - NF
#print SNR
return signal + 10**(-SNR/20.) * np.random.normal(size=signal.size)
Question 3: Signal Strength and Phase¶
GPS satellites have limited power and need to spread their signals over the entire surface of the earth, so the signals are very weak by the time they get to the GPS receiver. As a result, thermal noise and noise from other sources will be large compared to the signal. The code below plots the received signal in the time domain. There is a slider on the bottom that you can move around to boost the signal to noise ratio (SNR) in dB. The SNR measures exactly what you would expect it to: what is the ratio of actual signal to noise in the received message. As an analogy, think of yourself talking to a friend in a loud, crowded room. In order for your friend to hear you, you most likely have to speak very loudly to be heard over the background noise. Imagine what you would have to do to be heard from across the room! In a similar fashion, as you increase your SNR, you are more likely to get your signal across successfully. However, just as you need to exert more energy to speak louder, this also requires more power on the satellite's end.
NOTE: The slider in the following code will not work inline!¶
%pylab
# from nbviewer.ipython.org
from matplotlib.widgets import Slider
fig, ax = plt.subplots()
fig.subplots_adjust(bottom=0.2, left=0.1)
x = np.linspace(0, 1023, len(ca_canonical))
line, = plt.plot(x, [0.]*len(x))
ax.set_xlim([0, 1023])
ax.set_ylim([-5,5])
def on_change(val):
line.set_ydata(transmit_to_earth(ca_canonical, SNR_boost=val))
on_change(0)
slider_ax = plt.axes([0.1, 0.1, 0.8, 0.02])
slider = Slider(slider_ax, "Noise Figure", 0, 50, valinit=0, color="#AAAAAA")
slider.on_changed(on_change)
print "Look for offset = " + str(offset)
3a: By approximately how much do you need to boost the SNR for the received signal to look "clean"? What was the original SNR of the signal?¶
This is subjective, but there should be some SNR where it stops looking like garbage and starts looking like the signal. Is it reasonable to ask a satellite to use this much more power?
3a. Your answer here¶
The next problem is that when the GPS first starts up and hears a signal, it doesn't know when the data starts.
Note that transmit_to_earth() "rolls" the input by a randomly generated offset in order to simulate the fact that a GPS receiver doesn't know where the bits start and end.
Once a receiver knows this time offset, it knows the time to $<1$ms (unfortunately, light goes really far in a millisecond).
The next step is for the receiver to take each group of 1023 samples and figure out if they correspond to a 1 bit or a 0 bit.
A GPS receiver needs to do all of these tasks despite the signal being weaker than the noise!
The basic tool for achieving these tasks is the matched filter (http://en.wikipedia.org/wiki/Matched_filter). Matched filters perform a correlation on an input signal with an expected reference signal. A matched filter performs a convolution with the time-reversed, conjugated signal, which essentially amounts to a sliding dot product (remember, convolution time-reverses and conjugates the signal, generally, so if you time-reverse and conjugate in the first place, then the operation becomes a simple sliding dot product). The idea is that this sliding dot product will in general be small, until the two signals precisely align, where you will see a spike. If the two signals are aligned, $\sum_{i=0}^N r_i * (b * r_i) = Nb$ (recall $r_i$ is $\pm 1$). If the two signals are not aligned, because we have chosen our sequence to look random, we say $r_i$ is approximately independent from $r_k$ if $k\ne i$, so $\sum_{i=0}^N r_i (b * r_{i+k})$ has expectation approximately 0.
3b. In the space below, implement a function that performs matched filtering, i.e. performs a correlation on signal and reference. It should be able to handle signal and reference being different sizes.¶
def matched_filter(signal, reference=ca_canonical):
# 3b. Your code here
pass
If you have correctly implemented matched_filter, the below code should plot the result of matched filtering your noisy signal. The slider on the bottom boosts (or reduces) the SNR. If you boost the SNR, you should see a peak at offset (your particular random offset is printed by the above code). Cool stuff!
%pylab
# from nbviewer.ipython.org
from matplotlib.widgets import Slider
fig, ax = plt.subplots()
fig.subplots_adjust(bottom=0.2, left=0.1)
x = np.linspace(0, 1023, len(ca_canonical))
line, = plt.plot(x, [0.]*len(x))
ax.set_xlim([0, 1023]), ax.set_ylim([0,80])
def on_change(val):
line.set_ydata(10*np.log10(matched_filter(transmit_to_earth(ca_canonical, SNR_boost=val))**2))
on_change(0)
slider_ax = plt.axes([0.1, 0.1, 0.8, 0.02])
slider = Slider(slider_ax, "SNR Boost", -10, 10, valinit=0, color="#AAAAAA")
slider.on_changed(on_change)
print "Look for offset = " + str(offset)
3c. When the matched filter is aligned with the input, the output is $X=Nb + \sum_{i=0}^N v_i$, where $v_i\sim N(0,\sigma^2)$ is some additional noise. For our value of $N=1023$, what is the variance of our estimator $\hat{b}=\frac{1}{N}X$? What is the SNR of $\hat{b}$? How much bigger is it than our original SNR? (Recall $b\in \{ -1, 1\}$). Based on Q1, is this enough to make our signal look clean?¶
3c. Your answer here¶
For the higher datarate GPS signals that give more precise timing information, $N$ is smaller and the noise averaging takes longer. To average out enough noise to get a good lock, GPS receivers need to correlate for a long time. This is the primary reason it can take a long time for your GPS to figure out where you are.
Noise Figure¶
So far, we have assumed that our receiver detects the signal perfectly. In reality, no receiver is perfect and designers must work around many nonidealities. One common problem is noise figure. Before converting a signal from analog to digital, receivers pass the signal through an amplifier to get the weak signal to a high enough level for sampling. Unfortunately, active components like amplifiers add their own noise to the system. The parameter that measures this noise is called noise figure—it measures how much extra noise an active component adds to a signal.
For the purposes of this lab, we can treat $SNR_{out}=SNR_{in} - NF$, where $SNR_{in}$ is the SNR of the signal before going through the amplifier, $NF$ is the noise figure of the amplifier, and $SNR_{out}$ is the SNR of the signal at the output of the amplifier. All values are in dB.
3d. Write code that generates 100 different random offsets. Use the noise_figure and offset parameter of transmit_to_earth to generate 100 different simulated signals with noise figures of 1dB and 8dB. Use your matched filter code to find the offsets for the two different noise figures. Which noise figure performs better? By how much?¶
# 3d. Your code here
3d. Your answer here¶
Great! Now you know how GPS signals are transmitted and received :D
$\mathcal{SCIENCE\ on\ the\ SIDE}$
Note: this section on relativistic corrections for satellites is optional
Keeping time to an extreme level of accuracy is the crux of the utility of GPS, but even infinite accuracy isn't enough. If engineers don't take into account both Einstein's theories of special and general Relativity, the whole system goes up in flames.
Consider the following simple calculations:
Let's say we want our GPS location to be accurate to within $15m$ on Earth. Since distances are measured from the satellite via the change in time of the satellite's clock and the GPS device's clock, multiplied by the speed of light, this implies that we need our device to keep time accurately at the level of $\frac{15m}{c} = \frac{15m}{3 \times 10^{8} \frac{m}{s}} \approx 50ns$.
Since the satellites with which the GPS device communicates with are orbitting the Earth (twice per day) at speeds of $14,000\ km/hr$, according to special relativity, the clocks on the satellites actually run slower relative to those on the Earth's surface according to $T_{sat} = \frac{T_{Earth}}{\sqrt{1 - \frac{v^c}{c^2}}}$. Plugging in the appropriatae values, we see that the satellites' clocks tick more slowly by about $7 \mu s$ per day.
However, according to general relativity, objects under the influence of relatively weaker gravitational fields experience time faster than those under stronger gravitational fields, according to $T_{sat} = \frac{T_{Earth}}{\sqrt{1 - \frac{2GM}{Rc^2}}}$. Given that these satellites are $20,000km$ above the Earth and that they experience approximately one-fourth the gravity as we do on Earth, the resulting rate at which time passes faster for the satellites is $45 \mu s$ per day.
Thus, we have that the net change in the amount of time satellites experience relative to us on Earth is $45 \mu s - 7 \mu s = \boxed{+38 \mu s / day}$.
Given that a $50ns$ error in keeping time corresponded to a distance error of $15m$, a $38\mu s$ error in keeping time corresponds to an error in location of more than $11km$. Even crazier is that this is the amount of error in location that builds up per day! Without taking relativity into consideration, GPS devices would be rendered useless within 2 minutes of being synchronized with the satellites' atomic clocks.

For more info on the awesomeness of Einstein's Theory of Relativity, see Wikipedia.
Fore some mind-boggling results due to relativity, see these paradoxes.
For more info about relativity in GPS, see this doc.
Warning: Time dilation may occur in your head while your brain works at relativistic speeds to contemplate these ideas!