FM(Factorization Machine)系列主要参考美团的《深入FFM原理与实践》这篇博客内容做介绍并实现,首先介绍一下原理
一.FM原理¶
大家可能用过sklearn中的这个多项式特征处理函数:sklearn.preprocessing.PolynomialFeatures,它作用是就是将原始特征扩展为多项式特征,比如原始特征为$a,b$,那么它会做如下扩展:
而FM的初衷便是对这组新特征做线性建模,一般地,它可以表示如下:
$$ y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^nw_{ij}x_ix_j $$FM通常不会对平方项建模(比如上面的$a^2,b^2$),这里$n$代表样本的特征数量,$x_i$是第$i$个特征值,$w_0,w_i,w_{ij}$是模型参数,到这里大家可能会有疑惑,我们干嘛不先通过多项式特征处理函数做转换,然后再接着做一个线性回归或者logistic回归之类的不就行了吗?那这个...FM拿它何用?如果按照刚刚的操作其实是有很大问题的,主要有两点问题:
(1)参数爆炸;
(2)高维稀疏;
第一点比较容易理解,对于$n$个特征,$w_{ij}$将会有$\frac{n(n-1)}{2}$项,形象点说就是平常随意用到的100个特征,扩展后将会有5000个,而参数越多,如果没有足够的数据做训练,模型很容易陷入过拟合,而对于第二点,经常处理离散特征的同学会很容易理解,比如下图
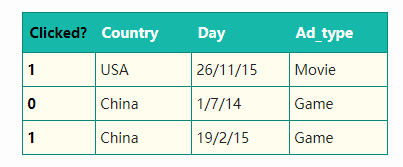
包含有三个特征(最左侧的是标签),且都是离散特征,而对于离散特征我们经常做的一种操作便是one-hot转换,转换后的结果如下图:

如果我们在对这些特征做多项式转换,可以发现转后的20多个特征中,仅仅只有3个非零特征,这就意味着绝大部分的$x_ix_j$将会是0,而损失函数关于$w_{ij}$的导数必然会包含有$x_ix_j$这一项,这就意味$w_{ij}$大部分情况下就是个摆设,很难被更新到,而FM便可以解决这两个问题,它假设$w_{ij}$由两个向量的内积生成:
$$ w_{ij}:=<v_i,v_j> $$这里,$v_i$表示第$i$个特征的隐向量,其向量长度为$k(k<<n)$,通常$k=4$即可,这时FM模型方程如下:
$$ y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n<v_i,v_j>x_ix_j $$进一步的,我们可以将其化简为如下形式:
$$ y(x)=w_0+\sum_{i=1}^nw_ix_i+\frac{1}{2}\sum_{f=1}^k((\sum_{i=1}^nv_{i,f}x_i)^2-\sum_{i=1}^nv_{i,f}^2x_i^2) $$这里,$v_{i,f}$表示向量$v_i$的第$f$个元素,上述化简用到了这样的关系:$ab+ac+bc=\frac{1}{2}((a+b+c)^2-(a^2+b^2+c^2))$,接下来我们可以进一步看看梯度:
$$ \frac{\partial}{\partial\theta}y(x)=\left\{\begin{matrix} 1 &\theta=w_0 \\ x_i &\theta=w_i \\ x_i\sum_{j=1}^nv_{j,f}x_j-v_{i,f}x_i^2 & \theta=v_{i,f} \end{matrix}\right. $$可以发现前面的两个问题可以被FM解决了,第一个问题,参数量从$n(n-1)/2$降低到了$kn$,第二个高维稀疏导致参数无法被训练的问题,对于$v_{i,f}$只要$x_i$不为0,且所有$x_j,j=1,2,...,n$中有一个不为0,那么梯度$\frac{\partial}{\partial v_{i,f}}y(x)$就不为0,这比$x_ix_j$不为0的条件松了很多
二.代码实现¶
这里就对FM应用到回归任务做简单实现,更多的功能扩展放到FFM中,下面推导一下损失函数对参数的梯度,假设样本$x$对应的标签为$t$,那么损失函数可以表示如下:
$$ L(\theta)=\frac{1}{2}(y(x)-t)^2 $$那么:
$$ \frac{\partial L(\theta)}{\partial y(x)}=y(x)-t $$再根据链式求导有:
$$ \frac{\partial L(\theta)}{\partial \theta}=\frac{\partial L(\theta)}{\partial y(x)}\frac{\partial y(x)}{\partial\theta}\\ =(y(x)-t)\cdot \left\{\begin{matrix} 1 &\theta=w_0 \\ x_i &\theta=w_i \\ x_i\sum_{j=1}^nv_{j,f}x_j-v_{i,f}x_i^2 & \theta=v_{i,f} \end{matrix}\right. $$"""
FM因子分解机的简单实现,只实现了损失函数为平方损失的回归任务,更多功能扩展请使用后续的FFM
代码封装到ml_models.fm中
"""
import numpy as np
class FM(object):
def __init__(self, epochs=1, lr=1e-3, adjust_lr=True, batch_size=1, hidden_dim=4, lamb=1e-3, alpha=1e-3,
normal=True, solver='adam', rho_1=0.9, rho_2=0.999, early_stopping_rounds=100):
"""
:param epochs: 迭代轮数
:param lr: 学习率
:param adjust_lr:是否根据特征数量再次调整学习率 max(lr,1/n_feature)
:param batch_size:
:param hidden_dim:隐变量维度
:param lamb:l2正则项系数
:param alpha:l1正则项系数
:param normal:是否归一化,默认用min-max归一化
:param solver:优化方式,包括sgd,adam,默认adam
:param rho_1:adam的rho_1的权重衰减,solver=adam时生效
:param rho_2:adam的rho_2的权重衰减,solver=adam时生效
:param early_stopping_rounds:对early_stopping进行支持,使用rmse作为评估指标,默认20
"""
self.epochs = epochs
self.lr = lr
self.adjust_lr = adjust_lr
self.batch_size = batch_size
self.hidden_dim = hidden_dim
self.lamb = lamb
self.alpha = alpha
self.solver = solver
self.rho_1 = rho_1
self.rho_2 = rho_2
self.early_stopping_rounds = early_stopping_rounds
# 初始化参数
self.w = None # w_0,w_i
self.V = None # v_{i,f}
# 归一化
self.normal = normal
if normal:
self.xmin = None
self.xmax = None
def _y(self, X):
"""
实现y(x)的功能
:param X:
:return:
"""
# 去掉第一列bias
X_ = X[:, 1:]
X_V = X_ @ self.V
X_V_2 = X_V * X_V
X_2_V_2 = (X_ * X_) @ (self.V * self.V)
pol = 0.5 * np.sum(X_V_2 - X_2_V_2, axis=1)
return X @ self.w.reshape(-1) + pol
def fit(self, X, y, eval_set=None, show_log=True):
X_o = X.copy()
if self.normal:
self.xmin = X.min(axis=0)
self.xmax = X.max(axis=0)
X = (X - self.xmin) / self.xmax
n_sample, n_feature = X.shape
x_y = np.c_[np.ones(n_sample), X, y]
# 记录loss
train_losses = []
eval_losses = []
# 调整一下学习率
if self.adjust_lr:
self.lr = max(self.lr, 1 / n_feature)
# 初始化参数
self.w = np.random.random((n_feature + 1, 1)) * 1e-3
self.V = np.random.random((n_feature, self.hidden_dim)) * 1e-3
if self.solver == 'adam':
# 缓存梯度一阶,二阶估计
w_1 = np.zeros_like(self.w)
V_1 = np.zeros_like(self.V)
w_2 = np.zeros_like(self.w)
V_2 = np.zeros_like(self.V)
# 更新参数
count = 0
best_eval_value = np.power(2., 1023)
eval_count = 0
for epoch in range(self.epochs):
np.random.shuffle(x_y)
for index in range(x_y.shape[0] // self.batch_size):
count += 1
batch_x_y = x_y[self.batch_size * index:self.batch_size * (index + 1)]
batch_x = batch_x_y[:, :-1]
batch_y = batch_x_y[:, -1:]
# 计算y(x)-t
y_x_t = self._y(batch_x).reshape((-1, 1)) - batch_y
# 更新w
if self.solver == 'sgd':
self.w = self.w - (self.lr * (np.sum(y_x_t * batch_x, axis=0) / self.batch_size).reshape(
(-1, 1)) + self.lamb * self.w + self.alpha * np.where(self.w > 0, 1, 0))
elif self.solver == 'adam':
w_reg = self.lamb * self.w + self.alpha * np.where(self.w > 0, 1, 0)
w_grad = (np.sum(y_x_t * batch_x, axis=0) / self.batch_size).reshape(
(-1, 1)) + w_reg
w_1 = self.rho_1 * w_1 + (1 - self.rho_1) * w_grad
w_2 = self.rho_2 * w_2 + (1 - self.rho_2) * w_grad * w_grad
w_1_ = w_1 / (1 - np.power(self.rho_1, count))
w_2_ = w_2 / (1 - np.power(self.rho_2, count))
self.w = self.w - (self.lr * w_1_) / (np.sqrt(w_2_) + 1e-8)
# 更新 V
batch_x_ = batch_x[:, 1:]
V_X = batch_x_ @ self.V
X_2 = batch_x_ * batch_x_
# 从i,f单个元素逐步更新有点慢
# for i in range(self.V.shape[0]):
# for f in range(self.V.shape[1]):
# if self.solver == "sgd":
# self.V[i, f] -= self.lr * (
# np.sum(y_x_t.reshape(-1) * (batch_x_[:, i] * V_X[:, f] - self.V[i, f] * X_2[:, i]))
# / self.batch_size + self.lamb * self.V[i, f] + self.alpha * (self.V[i, f] > 0))
# elif self.solver == "adam":
# v_reg = self.lamb * self.V[i, f] + self.alpha * (self.V[i, f] > 0)
# v_grad = np.sum(y_x_t.reshape(-1) * (
# batch_x_[:, i] * V_X[:, f] - self.V[i, f] * X_2[:, i])) / self.batch_size + v_reg
# V_1[i, f] = self.rho_1 * V_1[i, f] + (1 - self.rho_1) * v_grad
# V_2[i, f] = self.rho_2 * V_2[i, f] + (1 - self.rho_2) * v_grad * v_grad
# v_1_ = V_1[i, f] / (1 - np.power(self.rho_1, count))
# v_2_ = V_2[i, f] / (1 - np.power(self.rho_2, count))
# self.V[i, f] = self.V[i, f] - (self.lr * v_1_) / (np.sqrt(v_2_) + 1e-8)
# 从隐变量的维度进行更新
for f in range(self.V.shape[1]):
if self.solver == 'sgd':
V_grad = np.sum(
y_x_t.reshape((-1, 1)) * (batch_x_ * V_X[:, f].reshape((-1, 1)) - X_2 * self.V[:, f]),
axis=0)
self.V[:, f] = self.V[:, f] - self.lr * V_grad - self.lamb * self.V[:, f] - self.alpha * (
self.V[:, f] > 0)
elif self.solver == 'adam':
V_reg = self.lamb * self.V[:, f] + self.alpha * (self.V[:, f] > 0)
V_grad = np.sum(
y_x_t.reshape((-1, 1)) * (batch_x_ * V_X[:, f].reshape((-1, 1)) - X_2 * self.V[:, f]),
axis=0) + V_reg
V_1[:, f] = self.rho_1 * V_1[:, f] + (1 - self.rho_1) * V_grad
V_2[:, f] = self.rho_2 * V_2[:, f] + (1 - self.rho_2) * V_grad * V_grad
V_1_ = V_1[:, f] / (1 - np.power(self.rho_1, count))
V_2_ = V_2[:, f] / (1 - np.power(self.rho_2, count))
self.V[:, f] = self.V[:, f] - (self.lr * V_1_) / (np.sqrt(V_2_) + 1e-8)
# 计算eval loss
eval_loss = None
if eval_set is not None:
eval_x, eval_y = eval_set
eval_loss = np.std(eval_y - self.predict(eval_x))
eval_losses.append(eval_loss)
# 是否显示
if show_log:
train_loss = np.std(y - self.predict(X_o))
print("epoch:", epoch + 1, "/", self.epochs, ",samples:", (index + 1) * self.batch_size, "/",
n_sample,
",train loss:",
train_loss, ",eval loss:", eval_loss)
train_losses.append(train_loss)
# 是否早停
if eval_loss is not None and self.early_stopping_rounds is not None:
if eval_loss < best_eval_value:
eval_count = 0
best_eval_value = eval_loss
else:
eval_count += 1
if eval_count >= self.early_stopping_rounds:
print("---------------early_stopping-----------------------------")
break
return train_losses, eval_losses
def predict(self, X):
"""
:param X:
:return:
"""
if self.normal:
X = (X - self.xmin) / self.xmax
n_sample, n_feature = X.shape
X_V = X @ self.V
X_V_2 = X_V * X_V
X_2_V_2 = (X * X) @ (self.V * self.V)
pol = 0.5 * np.sum(X_V_2 - X_2_V_2, axis=1)
return np.c_[np.ones(n_sample), X] @ self.w.reshape(-1) + pol
三.测试¶
import matplotlib.pyplot as plt
%matplotlib inline
#造伪数据
data1 = np.linspace(1, 10, num=200)
data2 = np.linspace(1, 10, num=200) + np.random.random(size=200)
target = data1 * 2 + data2 * 1 + 10 * data1 * data2 + np.random.random(size=200)
data = np.c_[data1, data2]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.4, random_state=0)
#训练模型
model = FM()
train_losses,eval_losses = model.fit(X_train, y_train, eval_set=(X_test,y_test))
epoch: 1 / 1 ,samples: 1 / 120 ,train loss: 327.43304536928594 ,eval loss: 291.9721877542085 epoch: 1 / 1 ,samples: 2 / 120 ,train loss: 326.7160901918784 ,eval loss: 291.3271189485855 epoch: 1 / 1 ,samples: 3 / 120 ,train loss: 325.7151828483661 ,eval loss: 290.43528663690176 epoch: 1 / 1 ,samples: 4 / 120 ,train loss: 324.4152130238985 ,eval loss: 289.2810645127806 epoch: 1 / 1 ,samples: 5 / 120 ,train loss: 323.01897436328363 ,eval loss: 288.0444933403834 epoch: 1 / 1 ,samples: 6 / 120 ,train loss: 321.3838207470574 ,eval loss: 286.5995936954016 epoch: 1 / 1 ,samples: 7 / 120 ,train loss: 319.94927792261774 ,eval loss: 285.3310103840077 epoch: 1 / 1 ,samples: 8 / 120 ,train loss: 318.5719337115685 ,eval loss: 284.11400223694636 epoch: 1 / 1 ,samples: 9 / 120 ,train loss: 316.9476360205337 ,eval loss: 282.6800903373831 epoch: 1 / 1 ,samples: 10 / 120 ,train loss: 314.7864859352729 ,eval loss: 280.7747654767163 epoch: 1 / 1 ,samples: 11 / 120 ,train loss: 312.13341354273456 ,eval loss: 278.43789101462926 epoch: 1 / 1 ,samples: 12 / 120 ,train loss: 309.16581289509793 ,eval loss: 275.8247460891347 epoch: 1 / 1 ,samples: 13 / 120 ,train loss: 306.27255717177525 ,eval loss: 273.2781949183259 epoch: 1 / 1 ,samples: 14 / 120 ,train loss: 302.69416496771913 ,eval loss: 270.1306586526588 epoch: 1 / 1 ,samples: 15 / 120 ,train loss: 298.94444644455086 ,eval loss: 266.8335058027848 epoch: 1 / 1 ,samples: 16 / 120 ,train loss: 295.3143220143411 ,eval loss: 263.6423561128022 epoch: 1 / 1 ,samples: 17 / 120 ,train loss: 291.3237509064271 ,eval loss: 260.1354974551523 epoch: 1 / 1 ,samples: 18 / 120 ,train loss: 287.49921467259674 ,eval loss: 256.77523476633075 epoch: 1 / 1 ,samples: 19 / 120 ,train loss: 283.7042670379911 ,eval loss: 253.4414837569022 epoch: 1 / 1 ,samples: 20 / 120 ,train loss: 278.9662785039226 ,eval loss: 249.28103217515456 epoch: 1 / 1 ,samples: 21 / 120 ,train loss: 274.36280682169763 ,eval loss: 245.23921862961456 epoch: 1 / 1 ,samples: 22 / 120 ,train loss: 269.9916328968292 ,eval loss: 241.4018533233914 epoch: 1 / 1 ,samples: 23 / 120 ,train loss: 265.6497926902622 ,eval loss: 237.59063822710482 epoch: 1 / 1 ,samples: 24 / 120 ,train loss: 261.5304618788339 ,eval loss: 233.97503851467806 epoch: 1 / 1 ,samples: 25 / 120 ,train loss: 255.9712297539595 ,eval loss: 229.0974061155879 epoch: 1 / 1 ,samples: 26 / 120 ,train loss: 249.63664207715678 ,eval loss: 223.540478679283 epoch: 1 / 1 ,samples: 27 / 120 ,train loss: 243.5177699482245 ,eval loss: 218.1731976241854 epoch: 1 / 1 ,samples: 28 / 120 ,train loss: 235.93035644162356 ,eval loss: 211.51827263729555 epoch: 1 / 1 ,samples: 29 / 120 ,train loss: 228.29334367815406 ,eval loss: 204.8203973571134 epoch: 1 / 1 ,samples: 30 / 120 ,train loss: 221.0354471284559 ,eval loss: 198.45549752245287 epoch: 1 / 1 ,samples: 31 / 120 ,train loss: 213.95307377288907 ,eval loss: 192.2449043683773 epoch: 1 / 1 ,samples: 32 / 120 ,train loss: 207.1184199693237 ,eval loss: 186.25187133472122 epoch: 1 / 1 ,samples: 33 / 120 ,train loss: 200.57104162351598 ,eval loss: 180.5110271166571 epoch: 1 / 1 ,samples: 34 / 120 ,train loss: 194.30667243270833 ,eval loss: 175.01858282042767 epoch: 1 / 1 ,samples: 35 / 120 ,train loss: 185.93707682966206 ,eval loss: 167.68207164353436 epoch: 1 / 1 ,samples: 36 / 120 ,train loss: 175.7761789726375 ,eval loss: 158.77665170450192 epoch: 1 / 1 ,samples: 37 / 120 ,train loss: 164.91722726673692 ,eval loss: 149.26036101318223 epoch: 1 / 1 ,samples: 38 / 120 ,train loss: 154.08437475131961 ,eval loss: 139.76767558665097 epoch: 1 / 1 ,samples: 39 / 120 ,train loss: 143.8890967396074 ,eval loss: 130.8343368901387 epoch: 1 / 1 ,samples: 40 / 120 ,train loss: 132.60651489715613 ,eval loss: 120.94947293213396 epoch: 1 / 1 ,samples: 41 / 120 ,train loss: 122.05404130856687 ,eval loss: 111.70494507865556 epoch: 1 / 1 ,samples: 42 / 120 ,train loss: 112.12358484286929 ,eval loss: 103.00579214468047 epoch: 1 / 1 ,samples: 43 / 120 ,train loss: 102.89744660707402 ,eval loss: 94.92394460267941 epoch: 1 / 1 ,samples: 44 / 120 ,train loss: 91.42133543792461 ,eval loss: 84.87225024380368 epoch: 1 / 1 ,samples: 45 / 120 ,train loss: 78.13817406765556 ,eval loss: 73.23715667480447 epoch: 1 / 1 ,samples: 46 / 120 ,train loss: 65.70062355560859 ,eval loss: 62.33800496293836 epoch: 1 / 1 ,samples: 47 / 120 ,train loss: 54.02535849002556 ,eval loss: 52.094392295236844 epoch: 1 / 1 ,samples: 48 / 120 ,train loss: 41.683807766260934 ,eval loss: 41.22614231474926 epoch: 1 / 1 ,samples: 49 / 120 ,train loss: 30.433511697626553 ,eval loss: 31.185882623013303 epoch: 1 / 1 ,samples: 50 / 120 ,train loss: 21.514229448428743 ,eval loss: 22.771017028293713 epoch: 1 / 1 ,samples: 51 / 120 ,train loss: 17.16571530025454 ,eval loss: 17.13932905161945 epoch: 1 / 1 ,samples: 52 / 120 ,train loss: 19.682964325018517 ,eval loss: 16.627893626619425 epoch: 1 / 1 ,samples: 53 / 120 ,train loss: 26.17980787137188 ,eval loss: 20.579384922979518 epoch: 1 / 1 ,samples: 54 / 120 ,train loss: 33.98060706754525 ,eval loss: 26.580680020029057 epoch: 1 / 1 ,samples: 55 / 120 ,train loss: 40.718522653083056 ,eval loss: 32.11709555436113 epoch: 1 / 1 ,samples: 56 / 120 ,train loss: 47.1280969103238 ,eval loss: 37.51589197307846 epoch: 1 / 1 ,samples: 57 / 120 ,train loss: 53.23655823745947 ,eval loss: 42.72628701847929 epoch: 1 / 1 ,samples: 58 / 120 ,train loss: 57.91439837653235 ,eval loss: 46.7435156480082 epoch: 1 / 1 ,samples: 59 / 120 ,train loss: 62.2916257861008 ,eval loss: 50.517296176954176 epoch: 1 / 1 ,samples: 60 / 120 ,train loss: 63.37465187759853 ,eval loss: 51.453547885856835 epoch: 1 / 1 ,samples: 61 / 120 ,train loss: 62.79759163667555 ,eval loss: 50.95608888525005 epoch: 1 / 1 ,samples: 62 / 120 ,train loss: 62.14927336845161 ,eval loss: 50.397184853260356 epoch: 1 / 1 ,samples: 63 / 120 ,train loss: 58.68121179556597 ,eval loss: 47.407939684556275 epoch: 1 / 1 ,samples: 64 / 120 ,train loss: 54.521834742756766 ,eval loss: 43.83360698214427 epoch: 1 / 1 ,samples: 65 / 120 ,train loss: 50.152024574195885 ,eval loss: 40.09547496724038 epoch: 1 / 1 ,samples: 66 / 120 ,train loss: 44.39992720800713 ,eval loss: 35.213398197916526 epoch: 1 / 1 ,samples: 67 / 120 ,train loss: 39.333586356144004 ,eval loss: 30.969734556859894 epoch: 1 / 1 ,samples: 68 / 120 ,train loss: 34.594628478215704 ,eval loss: 27.079303861985274 epoch: 1 / 1 ,samples: 69 / 120 ,train loss: 30.59771443493049 ,eval loss: 23.897471633271614 epoch: 1 / 1 ,samples: 70 / 120 ,train loss: 27.012269759755636 ,eval loss: 21.175346759436962 epoch: 1 / 1 ,samples: 71 / 120 ,train loss: 24.206812085666503 ,eval loss: 19.193485550720503 epoch: 1 / 1 ,samples: 72 / 120 ,train loss: 21.92448958652032 ,eval loss: 17.744576448472227 epoch: 1 / 1 ,samples: 73 / 120 ,train loss: 20.28332003228646 ,eval loss: 16.855437337583528 epoch: 1 / 1 ,samples: 74 / 120 ,train loss: 19.048206816991755 ,eval loss: 16.332043336716456 epoch: 1 / 1 ,samples: 75 / 120 ,train loss: 18.153218019182912 ,eval loss: 16.097736138464715 epoch: 1 / 1 ,samples: 76 / 120 ,train loss: 17.62019020726425 ,eval loss: 16.078084905499313 epoch: 1 / 1 ,samples: 77 / 120 ,train loss: 17.276138511016793 ,eval loss: 16.184496145420404 epoch: 1 / 1 ,samples: 78 / 120 ,train loss: 17.095845317846123 ,eval loss: 16.35939284722499 epoch: 1 / 1 ,samples: 79 / 120 ,train loss: 17.01710369315616 ,eval loss: 16.582774084657874 epoch: 1 / 1 ,samples: 80 / 120 ,train loss: 17.010142091853233 ,eval loss: 16.78141646069649 epoch: 1 / 1 ,samples: 81 / 120 ,train loss: 17.039469465368413 ,eval loss: 16.983741883163493 epoch: 1 / 1 ,samples: 82 / 120 ,train loss: 17.09361648072788 ,eval loss: 17.183288214670156 epoch: 1 / 1 ,samples: 83 / 120 ,train loss: 17.103607965717508 ,eval loss: 17.215825153711435 epoch: 1 / 1 ,samples: 84 / 120 ,train loss: 17.054551444977335 ,eval loss: 17.058868161589743 epoch: 1 / 1 ,samples: 85 / 120 ,train loss: 17.002073634940558 ,eval loss: 16.763590578211996 epoch: 1 / 1 ,samples: 86 / 120 ,train loss: 17.0432834771113 ,eval loss: 16.429314526411407 epoch: 1 / 1 ,samples: 87 / 120 ,train loss: 17.20566174022564 ,eval loss: 16.206362628856045 epoch: 1 / 1 ,samples: 88 / 120 ,train loss: 17.454192113839586 ,eval loss: 16.086808426814954 epoch: 1 / 1 ,samples: 89 / 120 ,train loss: 17.810801283058517 ,eval loss: 16.047768615374864 epoch: 1 / 1 ,samples: 90 / 120 ,train loss: 18.352418415549227 ,eval loss: 16.11499606954419 epoch: 1 / 1 ,samples: 91 / 120 ,train loss: 18.949218549079465 ,eval loss: 16.281230192264882 epoch: 1 / 1 ,samples: 92 / 120 ,train loss: 19.745142441168305 ,eval loss: 16.591784659561966 epoch: 1 / 1 ,samples: 93 / 120 ,train loss: 20.56392873099257 ,eval loss: 16.981097554999526 epoch: 1 / 1 ,samples: 94 / 120 ,train loss: 21.492873758070026 ,eval loss: 17.483056184086117 epoch: 1 / 1 ,samples: 95 / 120 ,train loss: 22.638913137139614 ,eval loss: 18.166733085093927 epoch: 1 / 1 ,samples: 96 / 120 ,train loss: 23.784450245546704 ,eval loss: 18.903240572621787 epoch: 1 / 1 ,samples: 97 / 120 ,train loss: 25.096632758570667 ,eval loss: 19.79634156759791 epoch: 1 / 1 ,samples: 98 / 120 ,train loss: 26.379321474881408 ,eval loss: 20.708880523495196 epoch: 1 / 1 ,samples: 99 / 120 ,train loss: 27.730190859825026 ,eval loss: 21.703041579812098 epoch: 1 / 1 ,samples: 100 / 120 ,train loss: 29.024156936889867 ,eval loss: 22.680837567070597 epoch: 1 / 1 ,samples: 101 / 120 ,train loss: 30.446320541768557 ,eval loss: 23.778754692244608 epoch: 1 / 1 ,samples: 102 / 120 ,train loss: 31.90272032223926 ,eval loss: 24.923654288406865 epoch: 1 / 1 ,samples: 103 / 120 ,train loss: 33.25186049429429 ,eval loss: 25.999494771611396 epoch: 1 / 1 ,samples: 104 / 120 ,train loss: 34.67854715054938 ,eval loss: 27.150439790282746 epoch: 1 / 1 ,samples: 105 / 120 ,train loss: 34.645435697943064 ,eval loss: 27.123685246246136 epoch: 1 / 1 ,samples: 106 / 120 ,train loss: 34.68994743526686 ,eval loss: 27.159874803596903 epoch: 1 / 1 ,samples: 107 / 120 ,train loss: 34.81225420024342 ,eval loss: 27.259213281522232 epoch: 1 / 1 ,samples: 108 / 120 ,train loss: 34.93032281889466 ,eval loss: 27.355191146766472 epoch: 1 / 1 ,samples: 109 / 120 ,train loss: 35.214471007739654 ,eval loss: 27.58635316409818 epoch: 1 / 1 ,samples: 110 / 120 ,train loss: 35.65887123004236 ,eval loss: 27.94868223998747 epoch: 1 / 1 ,samples: 111 / 120 ,train loss: 35.95282974874901 ,eval loss: 28.188932498818 epoch: 1 / 1 ,samples: 112 / 120 ,train loss: 36.40533677831546 ,eval loss: 28.559526013999065 epoch: 1 / 1 ,samples: 113 / 120 ,train loss: 36.878308753734025 ,eval loss: 28.947889054255956 epoch: 1 / 1 ,samples: 114 / 120 ,train loss: 37.38011945871737 ,eval loss: 29.360998690623084 epoch: 1 / 1 ,samples: 115 / 120 ,train loss: 37.86842339837046 ,eval loss: 29.763993967202698 epoch: 1 / 1 ,samples: 116 / 120 ,train loss: 38.40383736296162 ,eval loss: 30.20691691837426 epoch: 1 / 1 ,samples: 117 / 120 ,train loss: 38.93430977980122 ,eval loss: 30.64680085481013 epoch: 1 / 1 ,samples: 118 / 120 ,train loss: 39.50290701669599 ,eval loss: 31.119384447400858 epoch: 1 / 1 ,samples: 119 / 120 ,train loss: 39.83255578849347 ,eval loss: 31.39391286683079 epoch: 1 / 1 ,samples: 120 / 120 ,train loss: 40.15889993779814 ,eval loss: 31.66603426567604
#查看拟合效果
plt.scatter(data[:, 0], target)
plt.plot(data[:, 0], model.predict(data), color='r')
[<matplotlib.lines.Line2D at 0x2dac366ed30>]
#查看loss
plt.plot(range(0,len(train_losses)),train_losses,label='train loss')
plt.plot(range(0,len(eval_losses)),eval_losses,label='eval loss')
plt.legend()
<matplotlib.legend.Legend at 0x2dadc90a8d0>