上一节主要基于PRML中10.3节的内容,利用变分推断实现了贝叶斯线性回归,并且效果还不错,但是呢,还留下了一个超参数$\beta$需要人工设定,这一节我们假设$\beta$也来源于一个Gamma分布,然后利用变分推断来求解,所以接下来的推导会和上一节有很多相同的地方,但为了完整性还是将这部分内容copy过来
一.联合概率分布¶
贝叶斯线性回归的图模型如下
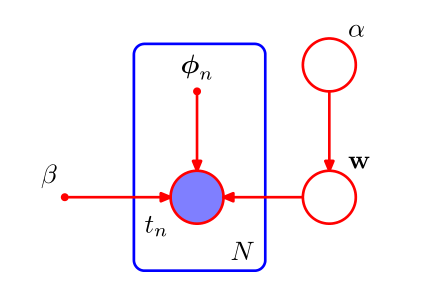 我们的似然函数和共轭先验可以假设如下:
我们的似然函数和共轭先验可以假设如下:
这里,$X=\{x_1,x_2,...,x_N\}$,$I$为单位矩阵,所以所有变量上的联合概率分布为:
$$ p(t,w,\alpha,\beta)=p(t\mid w,\beta)p(w\mid\alpha)p(\alpha)p(\beta) $$二.变分分布¶
接下来,我们就是要构建一个变分分布$q(w,\alpha,\beta)$去近似后验概率分布$p(w,\alpha,\beta\mid t)$,利用平均场假设,令:
$$ q(w,\alpha,\beta)=q(w)q(\alpha)q(\beta) $$根据VI第一节最后推导的公式,我们可以直接写出最优解:
$$ ln\ q^*(\alpha)=ln\ p(\alpha)+E_w[ln\ p(w\mid\alpha)]+const\\ =(a_0-1)ln\ \alpha-b_0\alpha+\frac{M}{2}ln\ \alpha-\frac{\alpha}{2}E[w^Tw]+const $$可以发现这个Gamma分布取对数的形式,通过观察系数项,我们有
$$ q^*(\alpha)=Gam(a\mid a_N,b_N) $$其中
$$ a_N=a_0+\frac{M}{2}\\ b_N=b_0+\frac{1}{2}E[w^Tw] $$同样的方式,我们可以求解$q^*(w)$:
$$ ln\ q^*(w)=E_\beta[ln\ p(t\mid w,\beta)]+E_\alpha[ln\ p(w\mid \alpha)]+const\\ =-\frac{E[\beta]}{2}\sum_{n=1}^N\left \{w^T\phi(x_n)-t_n\right \}^2-\frac{1}{2}E[\alpha]w^Tw+const\\ =-\frac{1}{2}w^T(E[\alpha]I+E[\beta]\Phi^T\Phi)w+E[\beta] w^T\Phi^Tt+const $$可以发现这是关于$w$的二次型,所以$q^*(w)$是一个高斯分布,通过配方可以得到:
$$ q^*(w)=N(w\mid m_N,S_N) $$其中
$$ m_N=E[\beta] S_N\Phi^Tt\\ S_N=(E[\alpha]I+E[\beta]\Phi^T\Phi)^{-1} $$可以发现,相比于上一节,$\alpha,\beta$分别变为了$E[\alpha],E[\beta]$
接下来就是$q^*(\beta)$:
$$ ln\ q^*(\beta)=ln\ p(\beta)+E_w[ln\ p(t\mid w,\beta)]+const\\ =(a_1-1)ln\ \beta-b_1\beta+\frac{N}{2}ln\ \beta-\frac{\beta}{2}E_w[(t-\Phi w^T)^T(t-\Phi w^T)] $$显然,这也是一个Gamma分布取对数的形式,它的形式如下:
$$
q^*(\beta)=Gam(\beta\mid a_M,b_M)
$$
其中
三.迭代求解¶
同样地,$q^*(w),q^*(\alpha),q^*(\beta)$之间互相耦合,$q^*(w)$中需要用到$E[\alpha],E[\beta]$,$q^*(\alpha)$中需要用到$E[w^Tw]$,而$q^*(\beta)$需要用到$E_w[(t-\Phi w^T)^T(t-\Phi w^T)]$,根据Gamma分布和高斯分布的性质,我们可以写出这几个期望的求解公式
$$ E[\alpha]=\frac{a_N}{b_N}\\ E[\beta]=\frac{a_M}{b_M}\\ E[w^Tw]=m_N^Tm_N+Tr(S_N)\\ E_w[(t-\Phi w^T)^T(t-\Phi w^T)]=E_w[w^T\Phi^T\Phi w]-2E_w[w^T\Phi^Tt]+t^Tt\\ =m_N^T\Phi^T\Phi m_N+Tr(\Phi S_N\Phi^T)-2m_N^T\Phi^Tt+t^Tt $$那么,我们初始随意为$E[\alpha],E[\beta]$赋予一个大于0的值,就可以迭代起来了:$E_0[\alpha]\rightarrow E_0[\beta]\rightarrow E_0[w^Tw]\rightarrow E_0[(t-\Phi w^T)^T(t-\Phi w^T)] \rightarrow \cdots$
四.预测分布¶
该过程与上一节一样
$$ p(\hat{t}\mid \hat{x},t)=\int p(\hat{t}\mid\hat{x},w)p(w\mid t)dw\\ \simeq \int p(\hat{t}\mid\hat{x},w)q(w)dw\\ =\int N(\hat{t}\mid w^T\phi(\hat{x}),\beta^{-1})N(w\mid m_N,S_N)dw\\ =N(\hat{t}\mid m_N^T\phi(\hat{x}),\sigma^2(\hat{x})) $$这里$\sigma^2(\hat{x})=\frac{1}{\beta}+\phi(\hat{x})^TS_N\phi(\hat{x})$
五.代码实现¶
"""
代码同样封装到ml_models.vi中,上一vi版本的类名改为LinearRegression1
"""
import numpy as np
import matplotlib.pyplot as plt
class LinearRegression(object):
def __init__(self, basis_func=None, tol=1e-5, epochs=100):
"""
:param basis_func: list,基函数列表,包括rbf,sigmoid,poly_{num},linear,fm,默认None为linear,其中poly_{num}中的{num}表示多项式的最高阶数,fm表示构建交叉因子
:param tol: 两次迭代参数平均绝对值变化小于tol则停止
:param epochs: 默认迭代次数
"""
if basis_func is None:
self.basis_func = ['linear']
else:
self.basis_func = basis_func
self.tol = tol
self.epochs = epochs
# 特征均值、标准差
self.feature_mean = None
self.feature_std = None
# 训练参数,也就是m_N
self.w = None
def _map_basis(self, X):
"""
将X进行基函数映射
:param X:
:return:
"""
n_sample, n_feature = X.shape
x_list = []
for basis_func in self.basis_func:
if basis_func == "linear":
x_list.append(X)
elif basis_func == "rbf":
x_list.append(np.exp(-0.5 * X * X))
elif basis_func == "sigmoid":
x_list.append(1 / (1 + np.exp(-1 * X)))
elif basis_func.startswith("poly"):
p = int(basis_func.split("_")[1])
for pow in range(1, p + 1):
x_list.append(np.power(X, pow))
elif basis_func == 'fm':
X_fm = np.zeros(shape=(n_sample, int(n_feature * (n_feature - 1) / 2)))
c = 0
for i in range(0, n_feature - 1):
for j in range(i + 1, n_feature):
X_fm[:, c] = X[:, i] * X[:, j]
c += 1
x_list.append(X_fm)
return np.concatenate(x_list, axis=1)
def fit(self, X, y):
self.feature_mean = np.mean(X, axis=0)
self.feature_std = np.std(X, axis=0) + 1e-8
X_ = (X - self.feature_mean) / self.feature_std
X_ = self._map_basis(X_)
X_ = np.c_[np.ones(X_.shape[0]), X_]
n_sample, n_feature = X_.shape
E_alpha = 1.0
E_beta = 1.0
current_w = None
for _ in range(0, self.epochs):
S_N = np.linalg.inv(E_alpha * np.eye(n_feature) + E_beta * X_.T @ X_)
self.w = E_beta * S_N @ X_.T @ y.reshape((-1, 1)) # 即m_N
if current_w is not None and np.mean(np.abs(current_w - self.w)) < self.tol:
break
current_w = self.w
# 更新 E_alph,E_beta
E_w = (self.w.T @ self.w)[0][0] + np.trace(S_N)
E_alpha = (n_feature - 1) / E_w # 这里假设a_0,b_0都为0
E_w_phi = np.dot(y.reshape(-1), y.reshape(-1)) + np.sum(X_ @ S_N * X_) + (self.w.T @ X_.T @ X_ @ self.w)[0][
0] - 2 * (self.w.T @ X_.T @ y.reshape((-1, 1)))[0][0]
E_beta = (n_sample - 1) / E_w_phi # 这里假设a_1,b_1都为0
# ml_models.vi包中,没有这一部分
return E_alpha, E_beta
def predict(self, X):
X_ = (X - self.feature_mean) / self.feature_std
X_ = self._map_basis(X_)
X_ = np.c_[np.ones(X_.shape[0]), X_]
return (self.w.T @ X_.T).reshape(-1)
def plot_fit_boundary(self, x, y):
"""
绘制拟合结果
:param x:
:param y:
:return:
"""
plt.scatter(x[:, 0], y)
plt.plot(x[:, 0], self.predict(x), 'r')
六.测试¶
#造伪样本
X=np.linspace(0,100,100)
X=np.c_[X,np.ones(100)]
w=np.asarray([3,2])
Y=X.dot(w)
X=X.astype('float')
Y=Y.astype('float')
X[:,0]+=np.random.normal(size=(X[:,0].shape))*3#添加噪声
Y=Y.reshape(100,1)
#加噪声
X=np.concatenate([X,np.asanyarray([[100,1],[101,1],[102,1],[103,1],[104,1]])])
Y=np.concatenate([Y,np.asanyarray([[3000],[3300],[3600],[3800],[3900]])])
%matplotlib inline
lr=LinearRegression()
alpha,beta=lr.fit(X[:,:-1],Y)
lr.plot_fit_boundary(X[:,:-1],Y)
alpha/beta
2.0081038570209815
可以发现L2正则化项的约束还没有证据近似的结果紧...,有些忧伤....,该问题留到后面再优化...