0.补充¶
在介绍高斯混合模型的变分推断之前先补充两个分布的知识,一个是高斯-Wishart分布,它是高维高斯分布的共轭先验,另一个是学生t分布,它是高斯-Gamma分布对精度积分的边缘概率分布,下面分别介绍
高斯-Wishart分布¶
对于$D$维向量$x$的多元高斯分布$N(x\mid\mu,\Lambda^{-1})$,假设精度$\Lambda$已知,则均值$\mu$的共轭先验分布仍为高斯分布,但对于均值已知,精度未知的情况,其共轭先验是Wishart分布,定义如下:
$$ \mathcal{W}(\Lambda\mid W,\mathcal{v})=B|\Lambda|^{\frac{\mathcal{v}-D-1}{2}}exp(-\frac{1}{2}Tr(W^{-1}\Lambda)) $$其中,$\mathcal{v}$被称为分布的自由度数量,$W$是一个$D\times D$的标量矩阵,$Tr(\cdot)$表示矩阵的迹,归一化系数$B$为:
$$ B(W,\mathcal{v})=|W|^{-\frac{\mathcal{v}}{2}}(2^{\frac{\mathcal {v}D}{2}}\pi^{\frac{D(D-1)}{4}}\prod_{i=1}^D\Gamma(\frac{\mathcal{v}+1-i}{2}))^{-1} $$而对于均值和精度均未知的情况,那么类似于一元变量的推理方法,可以得到其共轭先验为:
$$ p(\mu,\Lambda\mid\mu_0,beta,W,\mathcal{v})=N(\mu\mid\mu_0,(\beta\Lambda)^{-1})\mathcal{W}(\Lambda\mid W,\mathcal{v}) $$该分布便是高斯-Wishart分布,或者正态-Wishart分布
学生t分布¶
根据之前的推导我们知道,对于$\mu$已知,$\tau$未知的一元高斯分布$N(x\mid\mu,\tau^{-1})$,它的共轭分布为Gamma分布,不妨表示为$Gam(\tau\mid a,b)$,如果把精度积分掉,那么就得到了一个边缘概率分布:
$$ p(x\mid \mu,a,b)=\int_0^\infty N(x\mid\mu,\tau^{-1})Gam(\tau\mid a,b)d\tau\\ =\int_0^\infty \frac{b^ae^{(-b\tau)}\tau^{a-1}}{\Gamma(a)}(\frac{\tau}{2\pi})^{\frac{1}{2}}exp(-\frac{\tau}{2}(x-\mu)^2)d\tau\\ =\frac{b^a}{\Gamma(a)}(\frac{1}{2\pi})^{\frac{1}{2}}\int_0^\infty(\frac{z}{b+\frac{(x-\mu)^2}{2}})^{a-\frac{1}{2}}e^{-z}[b+\frac{(x-\mu)^2}{2}]^{-1}dz(令z=\tau(b+\frac{(x-\mu)^2}{2}))\\ =\frac{b^a}{\Gamma(a)}(\frac{1}{2\pi})^{\frac{1}{2}}(b+\frac{(x-\mu)^2}{2})^{-a-\frac{1}{2}}\int_0^\infty z^{(a+\frac{1}{2})-1}e^{-z}dz\\ =\frac{b^a}{\Gamma(a)}(\frac{1}{2\pi})^{\frac{1}{2}}(b+\frac{(x-\mu)^2}{2})^{-a-\frac{1}{2}}\Gamma(a+\frac{1}{2}) $$我们对参数做一下调整,令$\mathcal{v}=2a,\lambda=\frac{a}{b}$,那么这就是学生t分布:
$$ St(x\mid\mu,\lambda,\mathcal{v})=\frac{\Gamma(\frac{\mathcal{v}}{2}+\frac{1}{2})}{\Gamma(\frac{\mathcal{v}}{2})}(\frac{\lambda}{\pi\mathcal{v}})^{\frac{1}{2}}(1+\frac{\lambda(x-\mu)^2}{\mathcal{v}})^{-\frac{\mathcal{v}}{2}-\frac{1}{2}} $$这里,参数$\lambda$被称为t分布的精度(注意:通常情况下,它不是方差的倒数),参数$\mathcal{v}$被称为自由度,它的作用如下图所示(其中$\mu=0,\lambda=1$),对于$\mathcal{v}=1$的情况下,t分布是柯西分布,而对于$\mathcal{v}\rightarrow \infty$的情况下,t分布$St(x\mid\mu,\lambda,\mathcal{v})$就变成了高斯分布$N(x\mid\mu,\lambda^{-1})$
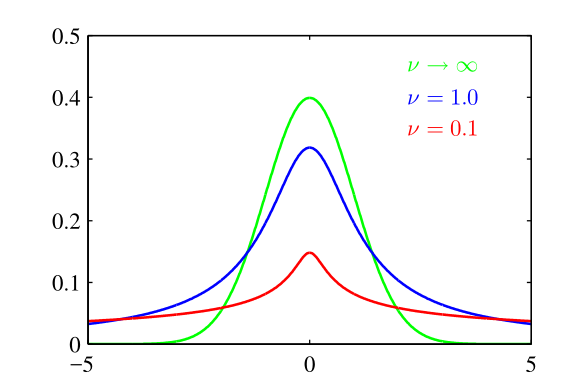
需要注意的一点是,学生t分布可以看作无限个同均值不同精度的高斯分布相加所得到(高斯混合模型的极限),所以t分布通常有更长的“尾巴”,建模时具有更强的鲁棒性,如下图是用t分布(红线)和高斯分布(绿线)建模的对比,在未引入噪声数据之前,如(a)图,t分布和高斯分布的建模效果相同,而在引入噪声数据之后,如(b)图,会对高斯分布模型造成较大的影响,而t分布几乎不受影响

高维学生t分布:
将一维学生t分布扩展到高维,可以写作
$$ St(x\mid\mu,\Lambda,\mathcal{v})=\frac{\Gamma(\frac{D}{2}+\frac{\mathcal{v}}{2})}{\Gamma(\frac{\mathcal{v}}{2})}\frac{|\Lambda|^{\frac{1}{2}}}{(\pi\mathcal{v})^{\frac{D}{2}}}[1+\frac{(x-\mu)^T\Lambda(x-\mu)}{\mathcal{v}}]^{-\frac{D}{2}-\frac{\mathcal{v}}{2}} $$其中,$D$是$x$的维度,另外t分布具有如下的性质:
(1)$E[x]=\mu,\mathcal{v}>1$;
(2)$cov[x]=\frac{\mathcal{v}}{\mathcal{v}-2}\Lambda^{-1},\mathcal{v}>2$;
(3)$mode[x]=\mu$
好的,补充内容差不多就是这些了,接下来按照上一节总结的四个步骤来介绍高斯混合模型的变分推断
一.联合概率分布¶
高斯混合模型的图模型如下图
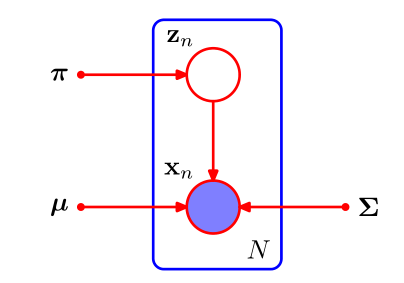
这里是概率图的盘式记法,其中,紫色实心的圈表示观测变量,红色空心圈表示隐变量(参数),框(盘子)内表示$N$次独立同分布的观测,接下来首先从似然函数出发,对于我们的每个观测$x_n$,都有一个对应的隐变量$z_n$,它是一个$K$维的二值向量,每个元素为$z_{nk},k=1,2,...,K$,表示对应的观测$x_n$是否采样于第$k$个高斯分布,对于给定的混合系数$\pi=\{\pi_1,\pi_2,...,\pi_K\}$(即每个高斯分布的权重系数),可以写出$Z={z_1,z_2,...,z_N}$关于$\pi$的条件概率分布:
$$ p(Z\mid\pi)=\prod_{n=1}^N\prod_{k=1}^K\pi_k^{z_{nk}} $$同样地,在给定了$Z,\mu,\Lambda=\Sigma^{-1}$的条件下,我们可以写出观测数据的条件概率分布:
$$ p(X\mid Z,\mu,\Lambda)=\prod_{n=1}^N\prod_{k=1}^KN(x_n\mid\mu_k,\Lambda_k^{-1})^{z_{nk}} $$这里,$\mu=\{\mu_k\},\Lambda=\{\Lambda_k\}$,这里使用精度矩阵是为了后面的计算方便,接下来引入参数$\mu,\Lambda,\pi$上的先验概率分布,显然为了计算简单,我们可以使用共轭先验,对于混合系数$\pi$的先验概率,我们可以使用狄利克雷分布:
$$ p(\pi)=Dir(\pi\mid\alpha_0)=C(\alpha_0)\prod_{k=1}^K\pi_k^{\alpha_0-1} $$这里,我们假设每个高斯分布的被观测的先验数量都一样为$\alpha_0$,$C(\alpha_0)$表示归一化系数,而对于$\mu,\Lambda$可以选择高斯-Wishart先验分布:
$$ p(\mu,\Lambda)=p(\mu\mid\Lambda)p(\Lambda)\\ =\prod_{k=1}^KN(\mu_k\mid m_0,(\beta_0\Lambda_k)^{-1})\mathcal{W}(\Lambda_k\mid W_0,\mathcal{v}_0) $$为了对称性,通常取$m_0=0$,注意,由于高斯-Wishart分布中$\mu$的概率分布的方差是$\Lambda$的函数,所以,这时的概率图模型需要被更新为如下形式:

根据概率图模型,我们将上面的几项乘起来就是联合概率分布咯:
$$ p(X,Z,\pi,\mu,\Lambda)=p(X\mid Z,\mu,\Lambda)p(Z\mid\pi)p(\pi)p(\mu\mid\Lambda)p(\Lambda) $$二.变分分布¶
上面推导出了联合概率分布,那么接下来就需要造一个变分分布去近似它的后验概率分布咯:
$$ q(Z,\pi,\mu,\Lambda)\rightarrow p(Z,\pi,\mu,\Lambda\mid X) $$接下来,我们做一个假设:变分分布可以在隐变量和参数之间记性分解,即:
$$ q(Z,\pi,\mu,\Lambda)=q(Z)q(\pi,\mu,\Lambda) $$注意,这里省略了下标,$q(Z)$与$q(\pi,\mu,\Lambda)$是不一样的分布,我们通过参数来区分不同的分布,接下来,就有:
$$ ln\ q^*(Z)=E_{\pi,\mu,\Lambda}[ln\ p(X,Z,\pi,\mu,\Lambda)]+const $$将上面,联合概率分布的表达式带入可得(将与$Z$无关的项整合到$const$中):
$$ ln\ q^*(Z)=E_\pi[ln\ p(Z\mid\pi)]+E_{\mu,\Lambda}[ln\ p(X\mid Z,\mu,\Lambda)]+const $$替换右侧的两个条件分布,然后再次把与$Z$无关的项整合到$const$中:
$$ ln\ q^*(Z)=\sum_{n=1}^N\sum_{k=1}^Kz_{nk}ln\ \rho_{nk}+const $$其中:
$$
ln\ \rho_{nk}=E[ln\ \pi_k]+\frac{1}{2}E[ln\ |\Lambda_k|]-\frac{D}{2}ln(2\pi)-\frac{1}{2}E_{\mu_k,\Lambda_k}[(x_n-\mu_k)^T\Lambda_k(x_n-\mu_k)]
$$
其中,$D$是观测变量$x$的维度,对上面的等式两边取指数,有:
$$ q^*(Z)\propto\prod_{n=1}^N\prod_{k=1}^K\rho_{nk}^{z_{nk}} $$由于,$q^*(Z)$需要是归一化的,而且同时$z_{nk},k=1,2,...,K$是二值的($K$个数中只有一个为1,其余为0),所以,我们有:
$$ q^*(Z)=\prod_{n=1}^N\prod_{k=1}^Kr_{nk}^{z_{nk}}\\ r_{nk}=\frac{\rho_{nk}}{\sum_{j=1}^K\rho_{nj}} $$对于离散情况有:
$$ E[z_{nk}]=r_{nk} $$可以发现,$q^*(Z)$的最优解是依赖于其他变量的,即它们是耦合的,需要使用迭代的方式进行求解,为了后面的推导方便,我们定义如下的三个量:
$$ N_k=\sum_{n=1}^Nr_{nk}\\ \bar{x}_k=\frac{1}{N_k}\sum_{n=1}^Nr_{nk}x_n\\ S_k=\frac{1}{N_k}\sum_{n=1}^Nr_{nk}(x_n-\bar{x}_k)(x_n-\bar{x}_k)^T $$大家可以发现,这里定义的这些量其实和EM算法中计算用到的量类似,接下来看看$q(\pi,\mu,\Lambda)$:
$$ ln\ q^*(\pi,\mu,\Lambda)=ln\ p(\pi)+\sum_{k=1}^Kln\ p(\mu_k,\Lambda_k)+E_Z[ln\ p(Z\mid\pi)]+\sum_{k=1}^K\sum_{n=1}^NE[z_{nk}]ln\ N(x_n\mid\mu_k,\Lambda_k^{-1})+const $$可以发现,表达式右边中一些项只与$\pi$相关,另外一些项只与$\mu$和$\Lambda$相关,也就是说$q(\pi,\mu,\Lambda)$还可以进一步分解为$q(\pi)q(\mu,\Lambda)$,而$q(\mu,\Lambda)$由可以分解为$k$与$\mu_k,\Lambda_k$相关的项,所以:
$$ q(\pi,\mu,\Lambda)=q(\pi)\prod_{k=1}^Kq(\mu_k,\Lambda_k) $$分离出与$\pi$相关的项,我们有:
$$ ln\ q^*(\pi)=(\alpha_0-1)\sum_{k=1}^Kln\ \pi_k+\sum_{k=1}^K\sum_{n=1}^Nr_{nk}ln\ \pi_k+const $$对上面的表达式两侧取指数可以发现,$q^*(\pi)$是一个狄利克雷分布:
$$ q^*(\pi)=Dir(\pi\mid\alpha),\alpha_k=\alpha_0+N_k $$最后,我们可以推出$q^*(\mu_k,\Lambda_k)$是一个高斯-Wishart分布:
$$ q^*(\mu_k,\Lambda_k)=N(\mu_k\mid m_k,(\beta_k\Lambda_k)^{-1})\mathcal{W}(\Lambda_k\mid W_k,\mathcal{v}_k) $$其中:
$$ \beta_k=\beta_0+N_k\\ m_k=\frac{1}{\beta_k}(\beta_0m_0+N_k\bar{x}_k)\\ W_k^{-1}=W_0^{-1}+N_kS_k+\frac{\beta_0N_k}{\beta_0+N_k}(\bar{x}_k-m_0)(\bar{x}_k-m_0)^T\\ \mathcal{v}_k=\mathcal{v}_0+N_k $$三.迭代更新¶
根据上面的推导,迭代更新流程就知道了:$r_{nk}\rightarrow \pi_k,\mu_k,\Lambda_k\rightarrow r_{nk}\rightarrow \cdots$,剩余还需要进一步求解的便是$r_{nk}$被归一化前的变量$\rho_{nk}$,它的计算公式,我们再写一下:
$$ ln\ \rho_{nk}=E[ln\ \pi_k]+\frac{1}{2}E[ln\ |\Lambda_k|]-\frac{D}{2}ln(2\pi)-\frac{1}{2}E_{\mu_k,\Lambda_k}[(x_n-\mu_k)^T\Lambda_k(x_n-\mu_k)] $$根据Wishart分布,狄利克雷分布的特性,我们可以得到:
$$ E[ln\ |\Lambda_k|]=\sum_{i=1}^D\psi(\frac{\mathcal{v}_k+1-i}{2})+Dln2+ln|W_k|\\ E[ln\ \pi_k]=\psi(\alpha_k)-\psi(\hat{\alpha}) $$这里$\hat{\alpha}=\sum_k\alpha_k$,$\psi(\cdot)$表示Digamma函数:
$$
\psi(a)=\frac{d}{da}ln\Gamma(a)
$$
另外,由高斯-Wishart分布,可以求得:
$$ E_{\mu_k,\Lambda_k}[(x_n-\mu_k)^T\Lambda_k(x_n-\mu_k)]=D\beta_k^{-1}+\mathcal{v}_k(x_n-m_k)^TW_k(x_n-m_k) $$四.变分分布的应用:概率密度预测¶
对于GMM,我们通常对新样本$\hat{x}$的概率密度感兴趣,根据贝叶斯推断理论,它的预测过程可以写作:
$$ p(\hat{x}\mid X)=\sum_{\hat{z}}\int\int\int p(\hat{x}\mid \hat{z},\mu,\Lambda)p(\hat{z}\mid \pi)p(\pi,\mu,\Lambda\mid X)d\pi d\mu d\Lambda\\ =\sum_{k=1}^K\int\int\int \pi_kN(\hat{x}\mid \mu_k,\Lambda_k^{-1})p(\pi,\mu,\Lambda\mid X)d\pi d\mu d\Lambda(消去\hat{x})\\ \simeq \sum_{k=1}^K\int\int\int \pi_kN(\hat{x}\mid \mu_k,\Lambda_k^{-1})q(\pi)q(\mu_k,\Lambda_k)d\pi d\mu_k d\Lambda_k(变分分布替换后验分布)\\ =\frac{1}{\hat{\alpha}}\sum_{k=1}^K\alpha_kSt(\hat{x}\mid m_k,L_k,\mathcal{v}_k+1-D) $$我们最终发现,概率密度其实是学生t分布的混合,其中:
$$ L_k=\frac{(\mathcal{v}_k+1-D)\beta_k}{1+\beta_k}W_k $$各符号的意义与前面推导的一致
五.代码实现¶
首先,我们将几个分布的函数写一下
import numpy as np
from scipy import special
import matplotlib.pyplot as plt
%matplotlib inline
"""
代码封装到utils中
"""
def dirichlet(u, alpha):
"""
狄利克雷分布
:param u: 随机变量
:param alpha: 超参数
:return:
"""
# 计算归一化因子
beta = special.gamma(np.sum(alpha))
for alp in alpha:
beta /= special.gamma(np.sum(alp))
rst = beta
# 计算结果
for idx in range(0, len(alpha)):
rst *= np.power(u[idx], alpha[idx] - 1)
return rst
def wishart(Lambda, W, v):
"""
wishart分布
:param Lambda:随机变量
:param W:超参数
:param v:超参数
:return:
"""
# 维度
D = W.shape[0]
# 先计算归一化因子
B = np.power(np.linalg.det(W), -1 * v / 2)
B_ = np.power(2.0, v * D / 2) * np.power(np.pi, D * (D - 1) / 4)
for i in range(1, D + 1):
B_ *= special.gamma((v + 1 - i) / 2)
B = B / B_
# 计算剩余部分
rst = B * np.power(np.linalg.det(Lambda), (v - D - 1) / 2)
rst *= np.exp(-0.5 * np.trace(np.linalg.inv(W) @ Lambda))
return rst
def St(X, mu, Lambda, v):
"""
学生t分布
:param X: 随机变量
:param mu: 超参数
:param Lambda: 超参数
:param v: 超参数
:return:
"""
n_sample, D = X.shape
return special.gamma(D / 2 + v / 2) * np.power(np.linalg.det(Lambda), 0.5) * np.power(
1 + np.sum((X - mu) @ Lambda * (X - mu), axis=1) / v, -1.0 * D / 2 - v / 2) / special.gamma(v / 2) / np.power(
np.pi * v, D / 2)
接下里就是模型代码了...
import os
os.chdir('../')
from ml_models import utils
"""
高斯混合模型的变分推断实现,封装到ml_models.vi中
"""
class GMMCluster(object):
def __init__(self, n_components=1, tol=1e-6, n_iter=100, prior_dirichlet_alpha=None, prior_gaussian_mean=None,
prior_gaussian_beta=None, prior_wishart_w=None, prior_wishart_v=None,
verbose=False):
"""
GMM的VI实现
:param n_components: 高斯混合模型数量
:param tol: -log likehold增益<tol时,停止训练
:param n_iter: 最多迭代次数
:prior_dirichlet_alpha:先验狄利克雷分布的超参数
:prior_gaussian_mean:先验高斯分布的均值
:prior_gaussian_beta:先验高斯分布的beta值,即精度前的系数
:prior_wishart_w:先验wishart分布的w
:prior_wishart_v:先验wishart分布的v
:param verbose: 是否可视化训练过程
"""
self.n_components = n_components
self.tol = tol
self.n_iter = n_iter
self.verbose = verbose
self.prior_dirichlet_alpha = prior_dirichlet_alpha
self.prior_gaussian_mean = prior_gaussian_mean
self.prior_gaussian_beta = prior_gaussian_beta
self.prior_wishart_w = prior_wishart_w
self.prior_wishart_v = prior_wishart_v
# 填充默认值
if self.prior_dirichlet_alpha is None:
self.prior_dirichlet_alpha_0 = np.asarray([1] * n_components)
self.prior_dirichlet_alpha = self.prior_dirichlet_alpha_0 + np.random.random(size=n_components) * 0.1
if self.prior_gaussian_beta is None:
self.prior_gaussian_beta_0 = np.asarray([1] * n_components)
self.prior_gaussian_beta = self.prior_gaussian_beta_0 + np.random.random(size=n_components) * 0.1
# 高斯模型参数
self.params = []
# 记录数据维度
self.D = None
def _init_params(self):
"""
初始化另一部分参数
:return:
"""
if self.prior_gaussian_mean is None:
self.prior_gaussian_mean_0 = np.zeros(shape=(self.n_components, self.D))
self.prior_gaussian_mean = self.prior_gaussian_mean_0 + np.random.random(
size=(self.n_components, self.D)) * 0.1
if self.prior_wishart_w is None:
self.prior_wishart_w_0 = [np.identity(self.D)] * self.n_components # 单位矩阵
self.prior_wishart_w = []
for w in self.prior_wishart_w_0:
self.prior_wishart_w.append(w + np.random.random(size=(self.D, self.D)) * 0.1)
if self.prior_wishart_v is None:
self.prior_wishart_v_0 = np.asarray([self.D] * self.n_components)
self.prior_wishart_v = self.prior_wishart_v_0 + np.random.random(size=self.n_components) * 0.1
def _update_single_step(self, X):
# 首先计算3个期望
E_ln_Lambda = []
for k in range(0, self.n_components):
value = self.D * np.log(2) + np.log(np.linalg.det(self.prior_wishart_w[k]))
for i in range(1, self.D + 1):
value += utils.special.digamma((self.prior_wishart_v[k] + 1 - i) / 2)
E_ln_Lambda.append(value)
E_ln_pi = []
hat_alpha = np.sum(self.prior_dirichlet_alpha)
for k in range(0, self.n_components):
E_ln_pi.append(utils.special.digamma(self.prior_dirichlet_alpha[k]) - utils.special.digamma(hat_alpha))
E_mu_Lambda = []
for k in range(0, self.n_components):
value = self.D * (1.0 / self.prior_gaussian_beta[k]) + np.sum(self.prior_wishart_v[k] * (
X - self.prior_gaussian_mean[k]) @ self.prior_wishart_w[k] * (X - self.prior_gaussian_mean[k]), axis=1)
E_mu_Lambda.append(value)
# 然后计算 r_nk
rho_n_k = []
for k in range(0, self.n_components):
value = np.exp(E_ln_pi[k] + 0.5 * E_ln_Lambda[k] - self.D / 2.0 * np.log(2 * np.pi) - 0.5 * E_mu_Lambda[k])
rho_n_k.append(value)
rho_n_k = np.asarray(rho_n_k).T
r_n_k = rho_n_k / np.sum(np.asarray(rho_n_k), axis=1, keepdims=True)
# 然后计算N_k,\bar{x}_k,S_k
N_k = np.sum(r_n_k, axis=0)
x_k = []
for k in range(0, self.n_components):
x_k.append(np.sum(r_n_k[:, [k]] * X, axis=0) / N_k[k])
S_k = []
for k in range(0, self.n_components):
S_k.append(np.transpose(r_n_k[:, [k]] * (X - x_k[k])) @ (r_n_k[:, [k]] * (X - x_k[k])) / N_k[k])
# 最后更新变分分布中的各个参数
for k in range(0, self.n_components):
self.prior_dirichlet_alpha[k] = self.prior_dirichlet_alpha_0[k] + N_k[k]
self.prior_gaussian_beta[k] = self.prior_gaussian_beta_0[k] + N_k[k]
self.prior_gaussian_mean[k] = 1.0 / self.prior_gaussian_beta[k] * (
self.prior_gaussian_beta_0[k] * self.prior_gaussian_mean_0[k] + N_k[k] * x_k[k])
W_k_inv = np.linalg.inv(self.prior_wishart_w_0[k]) + N_k[k] * S_k[k] + (self.prior_gaussian_beta_0[k] * N_k[
k]) / (self.prior_gaussian_beta_0[k] + N_k[k]) * np.transpose(
x_k[k] - self.prior_gaussian_mean_0[k]) @ (x_k[k] - self.prior_gaussian_mean_0[k])
self.prior_wishart_w[k] = np.linalg.inv(W_k_inv)
self.prior_wishart_v[k] = self.prior_wishart_v_0[k] + N_k[k]
def fit(self, X):
n_sample, n_feature = X.shape
self.D = n_feature
self._init_params()
last_rst = np.zeros(n_sample)
# 迭代训练
for _ in range(0, self.n_iter):
self._update_single_step(X)
if self.verbose:
utils.plot_contourf(X, lambda x: self.predict_sample_generate_proba(x), lines=5)
utils.plt.pause(0.1)
utils.plt.clf()
current_rst = self.predict_sample_generate_proba(X)
if np.mean(np.abs(current_rst - last_rst)) < self.tol:
break
last_rst = current_rst
if self.verbose:
utils.plot_contourf(X, lambda x: self.predict_sample_generate_proba(x), lines=5)
utils.plt.show()
def predict_proba(self, X):
# 预测样本在几个St上的概率分布
_, D = X.shape
hat_alpha = np.sum(self.prior_dirichlet_alpha)
W = np.asarray([utils.St(X, self.prior_gaussian_mean[k],
(self.prior_wishart_v[k] + 1 - D) / (1 + self.prior_gaussian_beta[k]) *
self.prior_wishart_w[k] * self.prior_gaussian_beta[k],
self.prior_wishart_v[k] + 1 - D) * self.prior_dirichlet_alpha[
k] / hat_alpha for k in range(0, self.n_components)]).T
W = W / np.sum(W, axis=1, keepdims=True)
return W
def predict(self, X):
# 预测样本最有可能产生于那一个高斯模型
return np.argmax(self.predict_proba(X), axis=1)
def predict_sample_generate_proba(self, X):
# 返回样本的生成概率
_, D = X.shape
hat_alpha = np.sum(self.prior_dirichlet_alpha)
W = np.asarray([utils.St(X, self.prior_gaussian_mean[k],
(self.prior_wishart_v[k] + 1 - D) / (1 + self.prior_gaussian_beta[k]) *
self.prior_wishart_w[k] * self.prior_gaussian_beta[k],
self.prior_wishart_v[k] + 1 - D) * self.prior_dirichlet_alpha[
k] / hat_alpha for k in range(0, self.n_components)]).T
return np.sum(W, axis=1)
测试...
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=400, centers=4, cluster_std=0.55, random_state=0)
X = X[:, ::-1]
#训练,查看收敛过程可以设置verbose=True
gmm = GMMCluster(verbose=False, n_iter=100, n_components=4)
gmm.fit(X)
#查看效果
utils.plot_contourf(X,gmm.predict_sample_generate_proba,lines=5)
D:\app\Anaconda3\lib\site-packages\matplotlib\contour.py:967: UserWarning: The following kwargs were not used by contour: 'linewidth' s)
#查看分类边界
utils.plot_decision_function(X,gmm.predict(X),gmm)
可以发现VI的收敛效果还是不错的,接下来再做一个测试,假如初始的n_components设置很大会怎样
gmm = GMMCluster(verbose=False, n_iter=100, n_components=20)
gmm.fit(X)
utils.plot_contourf(X,gmm.predict_sample_generate_proba,lines=5)
D:\app\Anaconda3\lib\site-packages\matplotlib\contour.py:967: UserWarning: The following kwargs were not used by contour: 'linewidth' s)
可以发现,上面设置初始聚类中心为20和设置为4的训练结果一样,说明VI训练的GMM对超参数并不敏感(这主要是由于引入了先验分布的缘故),所以我们不必再对超参数做交叉验证进行选择了....
六.总结一下¶
这一节完整的使用了四个步骤来做GMM的训练,虽然结果还OK,但我们需要更加清晰的认识到一个事实:如何对隐变量进行拆分,以及假设各变量子集服从何种分布是成功的关键,如果拆分方式不对,或者分布假设不对可能会取得比较差的结果(并没有做实验去检验...《机器学习》书上的观点)