一.原理推导¶
变分推断(VI)要做的事情很朴素,那就是有一个复杂的难以求解的分布,比如后验概率分布:$p(Z\mid X)$,这里$X$表示观测数据,$Z$表示参数或隐变量,VI就是利用一个简单可控的近似分布$q(Z)$去逼近目标$p(Z\mid X)$,即:
$$ q(Z)\rightarrow p(Z\mid X) $$比如下图,黄色区域便是我们的目标分布,红线和绿线是我们构建的高斯分布,去近似目标分布

那么,自然地有个问题就产生了,红线近似的更好还是绿线近似的更好?显然,上面的图我们很难肉眼区分的开,所以我们需要找到一个量化的指标来评估两个分布的近似程度,我们可以使用KL距离,它的定义如下:
$$ KL(q\mid\mid p)=\int q(Z)ln\{\frac{q(Z)}{p(Z\mid X)}\}dZ $$显然,当$q(Z)=p(Z\mid X)$时,$KL(q\mid\mid p)$取得最小值0,所以我们接下来求解下面优化问题就可以得到最优的近似分布$q^*(Z)$了:
$$ q^*(Z)=arg\min_{q(Z)}KL(q\mid\mid p) $$但是$KL$公式中同样还包含有$P(Z\mid X)$,这样我们在求解时依然会很困难,接下来我们推到一种等价的方式,我们首先可以将$p(X)$拆解为如下的等式:
$$ p(X)=\frac{p(X,Z)}{p(Z\mid X)} $$显然,上面的等式恒成立,然后对两边取对数,有:
$$ ln\ p(X)=ln\ p(X,Z)-ln\ p(Z\mid X) $$继续加入我们的$q(Z)$,有:
$$ ln\ p(X)=ln\ p(X,Z)-ln\ p(Z\mid X)\\ =ln\ \frac{p(X,Z)}{q(Z)}-ln\ \frac{p(Z\mid X)}{q(Z)} $$接下里,对两边求在近似分布$q(Z)$上的期望,由于左边与$Z$无关,求期望后还是其自身,所以:
$$ ln\ p(X)=\int q(Z)ln\{\frac{p(X,Z)}{q(Z)}\}dZ-\int q(Z)ln\{\frac{p(Z\mid X)}{q(Z)}\}dZ\\ =\int q(Z)ln\{\frac{p(X,Z)}{q(Z)}\}dZ+\int q(Z)ln\{\frac{p(q(Z)}{Z\mid X)}\}dZ\\ =\mathcal{L}(q)+KL(q\mid\mid p) $$这里,$\mathcal{L}$被称为证据下界(evidence lower bound,ELBO),这时,对数似然,ELBO以及KL距离三者之间具有如下的关系:
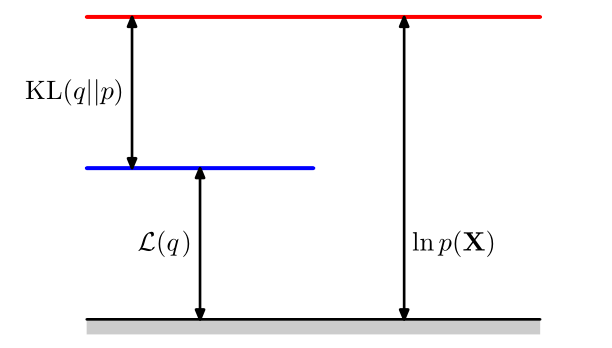
所以,对$KL(q\mid\mid p)$的极小化等价于对$\mathcal{L}(q)$做极大化,而ELBO函数中包含的联合概率分布$p(X,Z)$往往易于求解,所以,我们的最终计算目标便是:
$$ q^*(Z)=arg\max_{q(Z)}\int q(Z)ln\{\frac{p(X,Z)}{q(Z)}\}dZ $$二.对$q(Z)$进行简化¶
有时候,我们为了方便计算会将$Z$划分为若干个互不相交的组,每组记作$Z_i,i=1,2,...,M$(注意,每个$Z_i$可能包含多个变量),同时假设这些分组变量是相互独立的,那么有:
$$ q(Z)=\prod_{i=1}^Mq_i(Z_i) $$注意,这里每个$q_i(Z_i)$可以有不同的函数形式。接下来,我们考虑该形式下的最优解,由于上面的独立假设,我们对于$q(Z)$的优化问题,可以转换为依次对不同的$q_i(Z_i)$优化问题(其余的可以看做常数项,不会影响最优解),我们将上面的等式带入ELBO函数$\mathcal{L}(\cdot)$中,并分离出仅依赖于某一组因子的形式,比如$q_j(Z_j)$:
$$ \mathcal{L}(q)=\int\prod_i q_i(Z_i)[ln\ p(X,Z)-\sum_i ln\ q_i(Z_i)]dZ\\ =\int q_j(Z_j)[\int ln\ p(X,Z)\prod_{i\neq j}q_i(Z_i)dZ_i]dZ_j-\int q_j(Z_j)ln\ q_j(Z_j)dZ_j+const\\ =\int q_j(Z_j)ln\ \tilde{p}(X,Z_j)dZ_j-\int q_j(Z_j)ln\ q_j(Z_j)dZ_j\\ =-KL(q_j(Z_j)\mid\mid\tilde{p}(X,Z_j)) $$这里,我们定义:
$$ ln\ \tilde{p}(X,Z_j)=\int ln\ p(X,Z)\prod_{i\neq j}q_i(Z_i)dZ_i+const=E_{i\neq j}[ln\ p(X,Z)]+const $$这里$const$为常数项,最优解可以直接观测出来了,那就是使得$KL(q_j(Z_j)\mid\mid\tilde{p}(X,Z_j))$为0的解,那就只有两个分布相等情况下成立,即:
$$ q_j^*(Z_j)=\tilde{p}(X,Z_j)\\ $$消去$const$,可以写作如下:
$$ \tilde{p}(X,Z_j)=\frac{exp(E_{i\neq j}[ln\ p(X,Z)])}{\int exp(E_{i\neq j}[ln\ p(X,Z)])dZ_j}(const即是分母部分取负对数) $$通常,为了方便计算,用的更多的还是下面的表达式(下面的表达式后续会反复用到):
$$ ln\ q_j^*(Z_j)=E_{i\neq j}[ln\ p(X,Z)]+const $$因为对于复杂的计算,最后将多项的$const$合并在一起处理更为方便,因为它主要起着归一化系数的作用,而这个系数可以通过观测得出(比如上面等式中的分母项),不必刻意去计算。