这一节,我们不抛硬币了,来抛一抛骰子,首先让我们从抛一次骰子开始,假设该骰子共有$K$面(没说非要是6面...),显然每次的结果只能是这$K$种可能中的一种,我们可以将抛出的结果表示成一个$K$维的one-hot向量(仅有一个维度为1,其余维度全部为0的向量):
$$ x=(0,...,0,1,0,...)^T $$用参数$\mu_k$表示$x_k=1,k=1,2,...,K$的概率,所以全部的参数可以表示为:
$$ \mu=(\mu_1,\mu_2,...,\mu_K)^T $$由于要满足概率分布,所以有$\mu_k\geq 0,\sum_{k=1}^T\mu_k=1$,那么抛一次骰子的概率分布可以表示为:
$$ p(x\mid \mu)=\prod_{k=1}^K\mu_k^{x_k} $$一.多项分布¶
那么如果我们有$N$个骰子(参数相同),全部抛一次(相互独立),记出现第$k$面($k=1,2,...,K$)的次数为$m_k$,显然$m_k\geq 0,\sum_{k=1}^K=N$,那么关于$m_k$的的概率分布可以表示为:
$$ Mult(m_1,m_2,...,m_K\mid\mu,N)=\binom{N}{m_1m_2\cdots m_K}\prod_{k=1}^K\mu_k^{m_k} $$这便是多项式分布,其中归一化系数为:
$$ \binom{N}{m_1m_2\cdots m_K}=\frac{N!}{m_1!m_2!\cdots m_K!} $$直观上,归一化系数也很好理解,可以看做将$N$个骰子分成抛面数分别为$m_1,m_2,...,m_K$的$K$组的方案总数
极大似然估计¶
极大似然估计与前一节的求解类似,这里就直接写结果了:
$$ \mu_k^{ML}=\frac{m_k}{N} $$类似地,为了避免极大似然估计带来的过拟合问题,我们可以为$\mu$引入一个先验分布,通常选择狄利克雷分布作为多项式分布的先验分布...
二.狄利克雷分布¶
为什么是狄利克雷分布勒?因为它与多项式分布共轭,它包含有类似于$\prod_{k=1}^K\mu_k^{m_k}$的项,定义如下:
$$ Dir(\mu\mid\alpha)=\frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_K)}\prod_{k=1}^K\mu_k^{\alpha_k-1} $$其中,$\alpha=(\alpha_1,...,\alpha_K)^T,\alpha_0=\sum_{k=1}^K\alpha_k$,如下图,是三个变量的狄利克雷分布,左图是$\alpha=(0.1,0.1,0.1)^T$的情况,中图是$\alpha=(1,1,1)^T$的情况,右图是$\alpha=(10,10,10)^T$的情况:
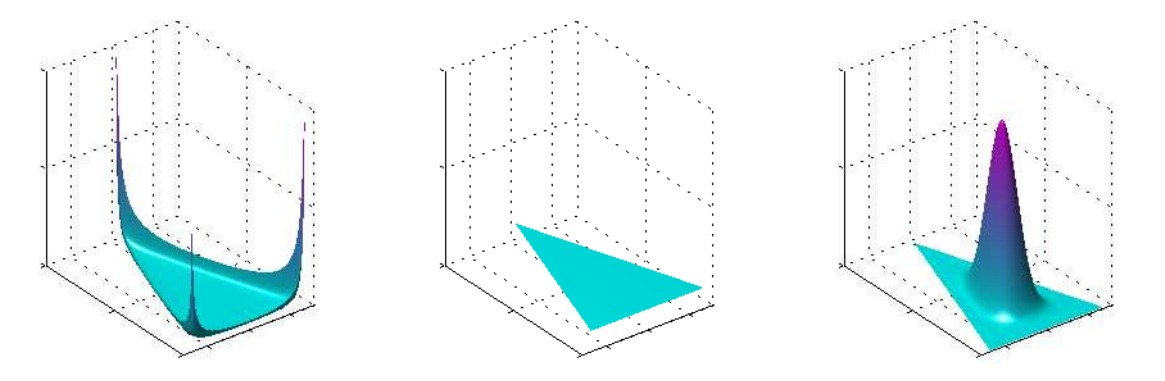
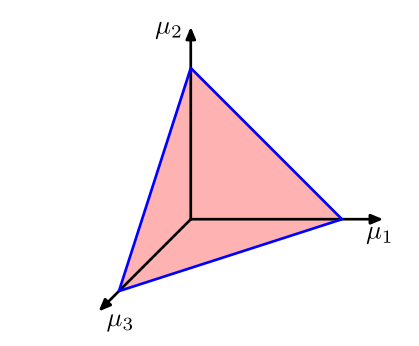
底部是$\mu_1,\mu_2,\mu_3$所张成的三角区域,由于需要满足$0\leq\mu_k \leq 1,\sum_{k=1}^3\mu_k=1$的条件,所以它们的取值范围只能被限制在一个三角区域内,该区域也是一个单纯形,如下图所示:
后验分布¶
显然,后验分布满足下面的关系:
$$ p(\mu\mid\alpha,m)\propto p(m\mid\mu)p(\mu\mid\alpha)\propto\prod_{k=1}^K\mu_k^{\alpha_k+m_k-1} $$所以,它也是一个狄利克雷分布,形式如下:
$$ p(\mu\mid\alpha,m)=Dir(\mu\mid\alpha+m)=\frac{\Gamma(N+\alpha_0)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)}\prod_{k=1}^K\mu_k^{\alpha_k+m_k-1} $$其中,$m=(m_1,...,m_K),\alpha=(\alpha_1,...,\alpha_K),N=\sum_{k=1}^Km_k,\alpha_0=\sum_{k=1}^K\alpha_k$
贝叶斯推断¶
有了后验分布,我们就可以做贝叶斯推断了
$$ p(x_k=1\mid m,\alpha)\\ =\int p(x_k=1\mid\mu)p(\mu\mid\alpha,m)d\mu\\ =\int\mu_k\frac{\Gamma(N+\alpha_0)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)}\prod_{i=1}^K\mu_i^{\alpha_i+m_i-1}d\mu\\ =\frac{\Gamma(N+\alpha_0)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)}\int\mu_k\prod_{i=1}^K\mu_i^{\alpha_i+m_i-1}d\mu\\ =\frac{\Gamma(N+\alpha_0)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)}\frac{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_k+m_k+1)\cdots\Gamma(\alpha_K+m_K)}{\Gamma(N+\alpha_0+1)}\\ =\frac{\Gamma(N+\alpha_0)}{\Gamma(\alpha_k+m_k)}\frac{\Gamma(\alpha_k+m_k+1)}{\Gamma(N+\alpha_0+1)}\\ =\frac{\alpha_k+m_k}{N+\alpha_0} $$