一.CRF的定义¶
条件随机场是给定随机变量$X$的条件下,随机变量$Y$的马尔科夫随机场。所以属于条件随机场的随机变量其实是$Y$,更加正式的定义如下:
设$X$与$Y$是随机变量,$P(Y\mid X)$是在给定$X$的条件下$Y$的条件概率分布。若随机变量$Y$构成一个由无向图$G=(V,E)$表示的马尔科夫随机场,即(下面是局部马尔科夫性的定义):
$$ P(Y_v\mid X,Y_w,w\neq v)=P(Y_v\mid X,Y_w,w\sim v) $$对任意节点$v$都成立,则称条件概率分布$P(Y\mid X)$为条件随机场。式中$w\sim v$表示在图$G=(V,E)$中与节点$v$有边直接相连的所有节点$w$,$w\neq v$表示节点$v$以外的所有节点,$Y_v$为节点$v$对应的随机变量,$Y_w$为节点集合$w$对应的随机变量。
二.线性链CRF的定义¶
对于处理序列标注问题,使用更多的是线性链条件随机场,如下图:
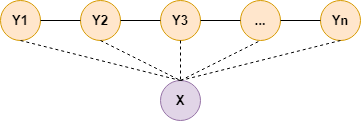
这里,$X=(X_1,X_2,...,X_n),Y=(Y_1,Y_2,...,Y_n)$均为线性链表示的随机变量序列,若在给定随机变量$X$的条件下,随机变量序列$Y$的条件概率分布$P(Y\mid X)$构成条件随机场,即满足如下的局部马尔可夫性:
$$ P(Y_i\mid X,Y_1,Y_2,...,Y_{i-1},Y_{i+1},...,Y-n)=P(Y_i\mid X,Y_{i-1},Y_{i+1}),i=1,2,..,n(在i=1或n时,只考虑单边) $$则称$P(Y\mid X)$为线性链条件随机场,在标注问题中,$X$表示输入观测序列,$Y$表示对应的输出标记序列。
三.CRF的参数化形式¶
由上一节的内容可以知道线性链CRF的$P(Y\mid X)$是构建在最大团$(Y_1,Y_2),(Y_2,Y_3),...,(Y_{n-1},Y_n)$之上的,那么还有一个问题就是最大团上的势函数如何定义呢?这里参考了对数线性模型的方式,即首先人工定义一系列的特征函数(指示函数),然后对其进行线性组合,最后做softmax(类比前面介绍的最大熵模型),而线性组合的各特征函数的权重便是CRF的参数,更加标准的定义如下:
设$P(Y\mid X)$为线性链条件随机场,则在随机变量$X$取值为$x$的条件下,随机变量$Y$取值为$y$的条件概率具有如下形式:
$$ P(y\mid x)=\frac{1}{Z(x)}exp(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum_{i,l}\mu_ls_l(y_i,x,i)) $$其中:
$$ Z(x)=\sum_yexp(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum_{i,l}\mu_ls_l(y_i,x,i)) $$这里,$t_k$是定义在边上的特征函数,称为转移特征,依赖于当前和前一个位置;$s_l$是定义在结点上的特征函数,称为状态特征,依赖于当前位置,而$\lambda_k,\mu_l$分为它们对应的权值,也就是CRF模型的参数
简化形式¶
上面的表达方式有些繁杂,特别是$\sum_{i,k}$以及$\sum_{i,l}$这两项,我们令$k=1,2,...,K_1,l=1,2,...,K_2,K=K_1+K_2$,对上面的公式做一些简化:
$$ \sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum_{i,l}\mu_ls_l(y_i,x,i)\\ =\sum_{k=1}^{K_1}\lambda_k[\sum_it_k(y_{i-1},y_i,x,i)]+\sum_{l=1}^{K_2}\mu_l[\sum_is_l(y_i,x,i)]\\ =[\lambda_1,..,\lambda_{K_1},\mu_1,..,\mu_{K_2}][\sum_it_1(y_{i-1},y_i,x,i),...,\sum_it_{K_1}(y_{i-1},y_i,x,i),\sum_is_1(y_i,x,i),...,\sum_is_{K_2}(y_i,x,i)]^T\\ =[w_1,..,w_K][f_1(y,x),...,f_K(y,x)]^T\\ =w^TF(y,x) $$其中:
$$ w_k=\left\{\begin{matrix} \lambda_k & k=1,2,...,K_1\\ \mu_l & k=K_1+l,l=1,2,...,K_2 \end{matrix}\right.\\ w=(w_1,w_2,...,w_K)^T $$$$ f_k(y,x)=\left\{\begin{matrix} \sum_it_k(y_{i-1},y_i,x,i) & k=1,2,...,K_1\\ \sum_is_l(y_i,x,i) & k=K_1+l,l=1,2,...,K_2 \end{matrix}\right.\\ F(y,x)=(f_1(y,x),f_2(y,x),...,f_K(y,x))^T $$所以,条件概率可以简写为:
$$ P(y\mid x)=\frac{1}{Z(x)}exp\sum_{k=1}^Kw_kf_k(y,x)\\ Z(x)=\sum_yexp\sum_{k=1}^Kw_kf_k(y,x) $$矩阵形式¶
如果只用上面的简化形式(给定$w$)对于求$P_w(y\mid x)$的分子项是OK滴,但是最麻烦的还是求分母项即:$Z_w(x)$,它可是要求所有的$y_i,i=1,2,..,n$的所有可能取值情况,假设它有$m$个状态,即$y_i\in \{q_1,q_2,..,q_{m}\},i=1,2,..,n$,那么:
$$ Z_w(x)=\sum_{y_1=q_1}^{q_m}\sum_{y_2=q_1}^{q_m}\cdots\sum_{y_n=q_1}^{q_m}exp(w^TF(y,x)) $$这个形式在HMM里面出现过了,时间复杂度还是指数级的$O(nm^n)$,参考HMM的处理方式,我们还是要将$w^TF(y,x)$转换成$\sum_{i=1}^n(\cdot)$的形式,这样才方便我们利用动态规划求解$Z_w(x)$,转换其实也很简单,上面的简化形式相当于先做$\sum_i$再做$\sum_k$,那我们这次交换一下次序先做$\sum_k$再做$\sum_i$就行哒,那么我们要先将$w^TF(y,x)$为$\sum_i\sum_k$的形式,然后再去掉$\sum_k$:
$$ w^TF(y,x)=\sum_{k=1}^Kw_kf_k(y,x)\\ =\sum_{k=1}^Kw_k\sum_{i=1}^nf_k(y_{i-1},y_i,x,i)\\ =\sum_{i=1}^n\sum_{k=1}^Kw_kf_k(y_{i-1},y_i,x,i)\\ =\sum_{i=1}^nW_i(y_{i-1},y_i\mid x) $$这里,$W_i(y_{i-1},y_i\mid x)=\sum_{k=1}^Kw_kf_k(y_{i-1},y_i,x,i)$,所以这时:
$$ Z_w(x)=\sum_{y_1=q_1}^{q_m}\sum_{y_2=q_1}^{q_m}\cdots\sum_{y_n=q_1}^{q_m}exp(\sum_{i=1}^n W_i(y_{i-1},y_i\mid x))\\ =\sum_{y_1=q_1}^{q_m}\sum_{y_2=q_1}^{q_m}\cdots\sum_{y_n=q_1}^{q_m}exp(W_1(y_0,y_1\mid x))exp(W_2(y_1,y_2\mid x))\cdots exp(W_n(y_{n-1},y_n\mid x)) $$到这里,可以嗅出熟悉的味道了吧,是不是和HMM中的概率计算很像了呢?将这里的$x$看做HMM中的$o$,将$y$看着HMM中的$i$,将$exp(W_1(y_0,y_1\mid x))$看做$b_{i1}(o_1)a_{i1i2}$,那求解方式不就是一回事了,使用动态回归就可以哒,下面叙述其过程:
(1)假设$y_i,i=1,2,..,n$共有$m$种取值$y_i\in \{q_1,q_2,...,q_{m}\}$,为了计算方便,我们为$y$引进特殊的起点和终点状态标记$y_0=start$和$y_{n+1}=stop$,不妨假设$start$和$stop$对应的状态为$q_0$和$q_{m+1}$,所以,现在$y_i$的取值状态多了2种,即$m+2$种
$$ M_i(x)=[M_i(q_o,q_t\mid x)]_{(m+2)\times(m+2)}\\ o,t=0,1,2,...,m,m+1 $$(2)对$i=1,2,3,...,n+1$,每一个位置构建一个$m+2$阶的矩阵:
这里,$[M_i(x)]_{o,t}=M_i(q_o,q_t\mid x)=exp(\sum_{k=1}^Kw_kf_k(q_o,q_t,x,i))$
$$ P_w(y\mid x)=\frac{1}{Z_w(x)}\prod_{i=1}^{n+1}M_i(y_{i-1},y_i\mid x)\\ Z_w(x)=[M_1(x)M_2(x)\cdots M_{n+1}(x)]_{0,m+1}$$(3)所以,通过DP,我们可以求得:
这里,下标$0,m+1$即是对应的$start$所在行,$stop$所在列的元素,另外由于$y$在头尾新增加了一个特征状态,所以$x$也可以在头尾对应新增加一个特殊占位符