一.维特比算法¶
隐状态预测是指在$P(O\mid\lambda)$给定的情况下,求一个隐状态序列$I$,使得$P(O,I\mid\lambda)$最大,比如下图,有三种隐状态,求在$O=(o_1,o_2,o_3,o_4)$的情况下,选择一条最优路径使得$P(O,I\mid\lambda)$最大,假设为图中的红色路径,那么最优路径为$i_1=q_1,i_2=q_2,i_3=q_1,i_4=q_3$
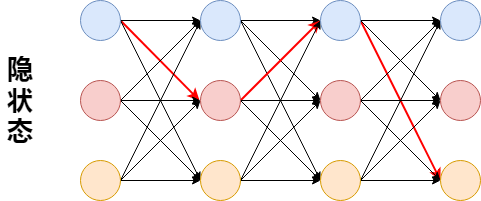
那如何求最优路径呢?下面这句话画个重点:
如果求得$i_1\rightarrow i_4$的最优路径为$i_1^*\rightarrow i_4^*$,那么$i_3^*\rightarrow i_4^*$必然为$i_3\rightarrow i_4$的最优路径
将时刻$t$状态为$i$的所有路径中的概率最大值表示为$\delta_t(i)$,那么在$\delta_3(1),\delta_3(2),\delta_3(3)$已知的情况下,要求$\delta_4(\cdot)$,我们只需在所有$i_3\rightarrow i_4$的9条路径中找出最优的一条即可,即这时可以将前面的看做黑箱即可
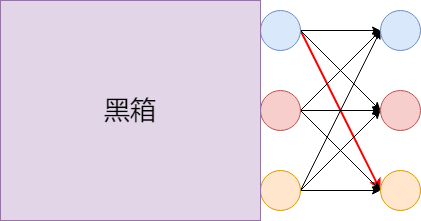
在$i_3\rightarrow i_4$这一步,我们是假设$\delta_3(\cdot)$已知了,那如何求解$\delta_3(\cdot)$呢?我们继续往前在$i_2\rightarrow i_3$的9条路径中选择即可,即:
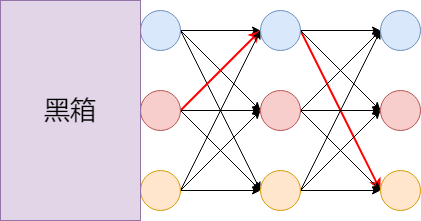
所以,递推关系就出来了:
$$ \delta_t(i)=\max_{1\leq j\leq N}[\delta_{t-1}(j)a_{ji}]b_i(o_t),i=1,2,..,N $$由于我们需要求得各节点的状态序列,所以还需要去保存我们的路径状态,从上面的递推过程也可以看出,我们在第$i_4$步的时候就可以确定使其最概率最大的第$i_3$步的取值了,所以我们做一个定义,在时刻$t$状态为$i$的所有单个路径$(i_1,i_2,...,i_{t-1},i_t)$中概率最大的路径的第$t-1$个节点为:
$$ \psi_t(i)=arg\max_{1\leq j\leq N}[\delta_{t-1}(j)a_{ji}],i=1,2,...,N $$接下来叙述完整的流程
算法流程¶
已知模型参数$\lambda=(A,B,\pi)$和观测数据$O=(o_1,o_2,...,o_T)$:
$$ \delta_1(i)=\pi_ib_i(o_1),i=1,2,...,N\\ \psi_t(i)=0,i=1,2,...,N $$(1)初始化
$$ \delta_t(i)=\max_{1\leq j\leq N}[\delta_{t-1}(j)a_{ji}]b_i(o_t),i=1,2,..,N\\ \psi_t(i)=arg\max_{1\leq j\leq N}[\delta_{t-1}(j)a_{ji}],i=1,2,...,N $$(2)递推,对$t=2,3,...,T$
$$ P^*=\max_{1\leq i\leq N}\delta_T(i)\\ i_T^*=arg\max_{1\leq i\leq N}[\delta_T(i)] $$(3)终止
$$ i_t^*=\psi_{t+1}(i_{t+1}^*) $$(4)回溯最优路径,对$t=T-1,T-2,...,1$
返回最优路径$I^*=(i_1^*,i_2^*,...,i_T^*)$
二.代码实现¶
继续在上一节的代码上添加...
import numpy as np
"""
隐马尔科夫模型实现,封装到ml_models.pgm
"""
class HMM(object):
def __init__(self, hidden_status_num=None, visible_status_num=None):
"""
:param hidden_status_num: 隐状态数
:param visible_status_num: 观测状态数
"""
self.hidden_status_num = hidden_status_num
self.visible_status_num = visible_status_num
# 定义HMM的参数
self.pi = None # 初始隐状态概率分布 shape:[hidden_status_num,1]
self.A = None # 隐状态转移概率矩阵 shape:[hidden_status_num,hidden_status_num]
self.B = None # 观测状态概率矩阵 shape:[hidden_status_num,visible_status_num]
def predict_joint_visible_prob(self, visible_list=None, forward_type="forward"):
"""
前向/后向算法计算观测序列出现的概率值
:param visible_list:
:param forward_type:forward前向,backward后向
:return:
"""
if forward_type == "forward":
# 计算初始值
alpha = self.pi * self.B[:, [visible_list[0]]]
# 递推
for step in range(1, len(visible_list)):
alpha = self.A.T.dot(alpha) * self.B[:, [visible_list[step]]]
# 求和
return np.sum(alpha)
else:
# 计算初始值
beta = np.ones_like(self.pi)
# 递推
for step in range(len(visible_list) - 2, -1, -1):
beta = self.A.dot(self.B[:, [visible_list[step + 1]]] * beta)
# 最后一步
return np.sum(self.pi * self.B[:, [visible_list[0]]] * beta)
def fit_with_hidden_status(self, visible_list, hidden_list):
"""
包含隐状态的参数估计
:param visible_list: [[],[],...,[]]
:param hidden_list: [[],[],...,[]]
:return:
"""
self.pi = np.zeros(shape=(self.hidden_status_num, 1))
self.A = np.zeros(shape=(self.hidden_status_num, self.hidden_status_num))
self.B = np.zeros(shape=(self.hidden_status_num, self.visible_status_num))
for i in range(0, len(visible_list)):
visible_status = visible_list[i]
hidden_status = hidden_list[i]
self.pi[hidden_status[0]] += 1
for j in range(0, len(hidden_status) - 1):
self.A[hidden_status[j], hidden_status[j + 1]] += 1
self.B[hidden_status[j], visible_status[j]] += 1
self.B[hidden_status[j + 1], visible_status[j + 1]] += 1
# 归一化
self.pi = self.pi / np.sum(self.pi)
self.A = self.A / np.sum(self.A, axis=0)
self.B = self.B / np.sum(self.B, axis=0)
def fit_without_hidden_status(self, visible_list=None, tol=1e-5, n_iter=10):
"""
不包含隐状态的参数估计:Baum-Welch算法
:param visible_list: [...]
:param tol:当pi,A,B的增益值变化小于tol时终止
:param n_iter:迭代次数
:return:
"""
# 初始化参数
if self.pi is None:
self.pi = np.ones(shape=(self.hidden_status_num, 1)) + np.random.random(size=(self.hidden_status_num, 1))
self.pi = self.pi / np.sum(self.pi)
if self.A is None:
self.A = np.ones(shape=(self.hidden_status_num, self.hidden_status_num)) + np.random.random(
size=(self.hidden_status_num, self.hidden_status_num))
self.A = self.A / np.sum(self.A, axis=0)
if self.B is None:
self.B = np.ones(shape=(self.hidden_status_num, self.visible_status_num)) + np.random.random(
size=(self.hidden_status_num, self.visible_status_num))
self.B = self.B / np.sum(self.B, axis=0)
for _ in range(0, n_iter):
# 计算前向概率
alphas = []
alpha = self.pi * self.B[:, [visible_list[0]]]
alphas.append(alpha)
for step in range(1, len(visible_list)):
alpha = self.A.T.dot(alpha) * self.B[:, [visible_list[step]]]
alphas.append(alpha)
# 计算后向概率
betas = []
beta = np.ones_like(self.pi)
betas.append(beta)
for step in range(len(visible_list) - 2, -1, -1):
beta = self.A.dot(self.B[:, [visible_list[step + 1]]] * beta)
betas.append(beta)
betas.reverse()
# 计算gamma值
gammas = []
for i in range(0, len(alphas)):
gammas.append((alphas[i] * betas[i])[:, 0])
gammas = np.asarray(gammas)
# 计算xi值
xi = np.zeros_like(self.A)
for i in range(0, self.hidden_status_num):
for j in range(0, self.hidden_status_num):
xi_i_j = 0.0
for t in range(0, len(visible_list) - 1):
xi_i_j += alphas[t][i][0] * self.A[i, j] * self.B[j, visible_list[t + 1]] * \
betas[t + 1][j][0]
xi[i, j] = xi_i_j
loss = 0.0 # 统计累计误差
# 更新参数
# 初始概率
for i in range(0, self.hidden_status_num):
new_pi_i = gammas[0][i]
loss += np.abs(new_pi_i - self.pi[i][0])
self.pi[i] = new_pi_i
# 隐状态转移概率
for i in range(0, self.hidden_status_num):
for j in range(0, self.hidden_status_num):
new_a_i_j = xi[i, j] / np.sum(gammas[:, i][:-1])
loss += np.abs(new_a_i_j - self.A[i, j])
self.A[i, j] = new_a_i_j
# 观测概率矩阵
for j in range(0, self.hidden_status_num):
for k in range(0, self.visible_status_num):
new_b_j_k = np.sum(gammas[:, j] * (np.asarray(visible_list) == k)) / np.sum(gammas[:, j])
loss += np.abs(new_b_j_k - self.B[j, k])
self.B[j, k] = new_b_j_k
# 归一化
self.pi = self.pi / np.sum(self.pi)
self.A = self.A / np.sum(self.A, axis=0)
self.B = self.B / np.sum(self.B, axis=0)
if loss < tol:
break
def predict_hidden_status(self, visible_list):
"""
维特比算法解码概率最大的隐状态
:param visible_list:
:return:
"""
# 初始化
delta = self.pi * self.B[:, [visible_list[0]]]
psi = [[0] * self.hidden_status_num]
# 递推
for visible_index in range(1, len(visible_list)):
new_delta = np.zeros_like(delta)
new_psi = []
# 当前节点
for i in range(0, self.hidden_status_num):
best_pre_index_i = -1
best_pre_index_value_i = 0
delta_i = 0
# 上一轮节点
for j in range(0, self.hidden_status_num):
delta_i_j = delta[j][0] * self.A[j, i] * self.B[i, visible_list[visible_index]]
if delta_i_j > delta_i:
delta_i = delta_i_j
best_pre_index_value_i_j = delta[j][0] * self.A[j, i]
if best_pre_index_value_i_j > best_pre_index_value_i:
best_pre_index_value_i = best_pre_index_value_i_j
best_pre_index_i = j
new_delta[i, 0] = delta_i
new_psi.append(best_pre_index_i)
delta = new_delta
psi.append(new_psi)
# 回溯
best_hidden_status = [np.argmax(delta)]
for psi_index in range(len(visible_list) - 1, 0, -1):
next_status = psi[psi_index][best_hidden_status[-1]]
best_hidden_status.append(next_status)
best_hidden_status.reverse()
return best_hidden_status
#用例10.3做测试
pi = np.asarray([[0.2], [0.4], [0.4]])
A = np.asarray([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
B = np.asarray([[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]])
hmm = HMM(hidden_status_num=3, visible_status_num=2)
hmm.pi = pi
hmm.A = A
hmm.B = B
print(hmm.predict_hidden_status([0, 1, 0]))
[2, 2, 2]