对于HMM的参数学习,其实分两种情况,第一种是训练数据包括了隐状态序列和观测状态序列,比如$S$个序列对:
$$ \{(O_1,I_1),(O_2,I_2),...,(O_S,I_S)\} $$另一种是训练数据仅包含了观测状态序列,而未包含隐状态序列,比如:
$$ \{O_1,O_2,...,O_S\} $$显然,两者均可使用极大似然估计进行参数求解,只是后者需要用到EM算法,下面分别对其做介绍
一.有监督的方法¶
这种情况就比较简单了,直接对数据做统计即可
1.1 转移概率$a_{ij}$的估计¶
假设样本中任意时刻$t$处于状态$i$在下一时刻转移到状态$j$的频数为$A_{ij}$,那么:
$$ a_{ij}=\frac{A_{ij}}{\sum_{j=1}^NA_{ij}},i=1,2,...,N,j=1,2,...,N $$1.2 观测概率$b_j(k)$的估计¶
假设样本中状态为$j$并且观测为$k$的频数为$B_{jk}$,那么:
$$ b_{jk}=\frac{B_{jk}}{\sum_{k=1}^MB_{jk}},j=1,2,...,N,k=1,2,...,M $$1.3 初始状态概率$\pi$分布¶
直接计算样本中初始隐状态$q_i,i=1,2,...,N$的频率即可
二.无监督的方法¶
这种情况我们可以使用EM算法,隐变量我们自然可以选择隐状态$I$咯,假设目前所有的观测数据为$O=(o_1,o_2,...,o_T)$,所有的隐数据为$I=(i_1,i_2,...,i_T)$,令$\lambda^-$是HMM参数的当前估计值,$\lambda$是需要极大化的HMM参数,那么$Q$函数我们就可以写出来了:
2. 1 写出Q函数¶
$$ Q(\lambda,\lambda^-)=\sum_IlogP(O,I\mid\lambda)P(O,I\mid\lambda^-) $$我们首先看看$P(O,I\mid\lambda)$,显然可以直接由HMM的概率图模型直接写出:
$$ P(O,I\mid\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)\cdots a_{i_{T-1}i_T}b_{i_T}(o_T) $$对于第二项,在Q函数中,它应该为$P(I\mid O,\lambda^-)$才对,但由于$P(I\mid O,\lambda^-)=\frac{P(I,O\mid\lambda^-)}{P(O\mid\lambda^-)}$中$P(O\mid\lambda^-)$为常数,对极大化$Q$函数没有影响
接下里,对Q函数化简:
$$ Q(\lambda\mid\lambda^-)=\sum_Ilog\pi_{i_1}P(O,I\mid\lambda^-)+\sum_I(\sum_{t=1}^{T-1}loga_{i_ti_{t+1}})P(O,I\mid\lambda^-)+\sum_I(\sum_{t=1}^Tlogb_{i_t}(o_t))P(O,I\mid\lambda^-) $$2.2 极大化Q函数¶
接下来便是极大化Q函数了,由于HMM的参数单独地出现在3个项中,所以我们需要对各项单独极大化即可
初始状态$\pi$的更新¶
第一项公式可以写作:
$$ \sum_Ilog\pi_{i_1}P(O,I\mid\lambda^-)=\sum_{i=1}^Nlog\pi_iP(O,i_1=i\mid\lambda^-)\\ s.t. \sum_{i=1}^N\pi_i=1 $$通过构造拉格朗日函数求KKT条件可以得到:
$$ \pi_i=\frac{P(O,i_1=i\mid\lambda^-)}{P(O\mid\lambda^-)},i=1,2,...,N $$隐状态概率矩阵$A$的更新¶
对于第二项:
$$ \sum_I(\sum_{t=1}^{T-1}loga_{i_ti_{t+1}})P(O,I\mid\lambda^-)=\sum_{i=1}^N\sum_{j=1}^N\sum_{t=1}^{T-1}loga_{ij}P(O,i_t=i,i_{t+1}=j\mid\lambda^-)\\ s.t. \sum_{j=1}^Na_{ij}=1,i=1,2,...,N $$同理,通过构造拉格朗日函数并求KKT条件可得:
$$ a_{ij}=\frac{P(O,i_t=i,i_{t+1}=j\mid\lambda^-)}{\sum_{t=1}^{T-1}P(O,i_t=i\mid\lambda^-)} $$观测状态概率矩阵$B$的更新¶
第三项:
$$ \sum_I(\sum_{t=1}^Tlogb_{i_t}(o_t))P(O,I\mid\lambda^-)=\sum_{j=1}^N\sum_{k=1}^M\sum_{t=1}^Tlogb_j(k)P(O,i_t=j\mid\lambda^-)I(o_t=v_k)\\ s.t.\sum_{k=1}^Mb_j(k)=1,j=1,2,..,M $$同理,求得:
$$ b_j(k)=\frac{\sum_{t=1}^TP(O,i_t=j\mid\lambda^-)I(o_t=v_k)}{\sum_{t=1}^TP(O,i_t=j\mid\lambda^-)} $$好的,到这里参数的求解就推导完了,接下里需要对上面的计算进行优化,我们发现上式的求解主要包含两种类型,一种是$P(O,i_t=i\mid\lambda^-)$的形式,另一种是$P(O,i_t=i,i_{t+1}=j\mid\lambda^-)$的形式,下面对其求解做介绍
2.3 $P(O,i_t=i\mid\lambda^-)$和$P(O,i_t=i,i_{t+1}=j\mid\lambda^-)$的求解¶
这里其实可以使用上一节介绍的前向概率$\alpha_t(i)$和后向概率$\beta_t(i)$求解(符号定义与上一节相同)
$P(O,i_t=i\mid\lambda^-)$的求解¶
对于$P(O,i_t=i\mid\lambda^-)$,其实上一节已经能给出答案了,它的求解如下图:
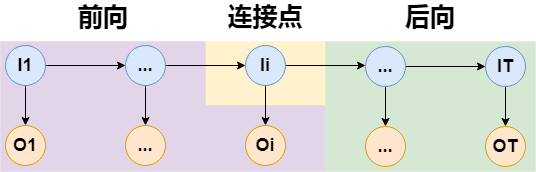
所以只需要将$t$时刻的前向概率和后向概率乘起来即可,令:
$$ \gamma_t(i)=P(O,i_t=i\mid\lambda^-)=\alpha_t(i)\beta_t(i) $$$P(O,i_t=i,i_{t+1}=j\mid\lambda^-)$的求解¶
对于$P(O,i_t=i,i_{t+1}=j\mid\lambda^-)$的求解,可以让后向概率往后退一步,如下图:
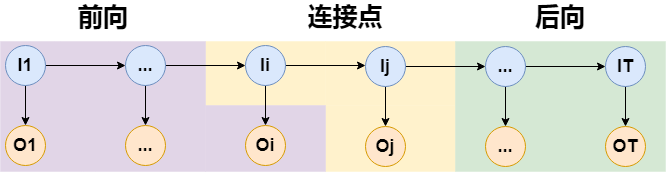
这样,我们可以方便将结果写出来,令:
$$ \xi_t(i,j)=P(O,i_t=i,i_{t+1}=j\mid\lambda^-)=\alpha_t(i)a_{ij}b_j(o_j)\beta_{t+1}(j) $$这便是Baum-Welch算法,接下来对上面的无监督学习过程做总结,并梳理出算法流程
2.4 Baum-Welch算法¶
已知观测数据$O=(o_1,o_2,...,o_T)$:
(1)初始化:对$n=0$,随机初始化 $a_{ij}^{(0)},b_j(k)^{(0)},\pi_i^{(0)}$(注意满足概率的约束条件)
$$ a_{ij}^n=\frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma_t(i)}\\ b_j(k)^n=\frac{\sum_{t=1}^T\gamma_t(j)I(o_t=v_k)}{\sum_{t=1}^T\gamma_t(j)}\\ \pi_i^n=\gamma_1(i) $$(2)递推,对$n=1,2,...$
(3)根据收敛条件进行终止
三.代码实现¶
让我们接着上一节的代码继续写...
import numpy as np
"""
隐马尔科夫模型实现,封装到ml_models.pgm
"""
class HMM(object):
def __init__(self, hidden_status_num=None, visible_status_num=None):
"""
:param hidden_status_num: 隐状态数
:param visible_status_num: 观测状态数
"""
self.hidden_status_num = hidden_status_num
self.visible_status_num = visible_status_num
# 定义HMM的参数
self.pi = None # 初始隐状态概率分布 shape:[hidden_status_num,1]
self.A = None # 隐状态转移概率矩阵 shape:[hidden_status_num,hidden_status_num]
self.B = None # 观测状态概率矩阵 shape:[hidden_status_num,visible_status_num]
def predict_joint_visible_prob(self, visible_list=None, forward_type="forward"):
"""
前向/后向算法计算观测序列出现的概率值
:param visible_list:
:param forward_type:forward前向,backward后向
:return:
"""
if forward_type == "forward":
# 计算初始值
alpha = self.pi * self.B[:, [visible_list[0]]]
# 递推
for step in range(1, len(visible_list)):
alpha = self.A.T.dot(alpha) * self.B[:, [visible_list[step]]]
# 求和
return np.sum(alpha)
else:
# 计算初始值
beta = np.ones_like(self.pi)
# 递推
for step in range(len(visible_list) - 2, -1, -1):
beta = self.A.dot(self.B[:, [visible_list[step + 1]]] * beta)
# 最后一步
return np.sum(self.pi * self.B[:, [visible_list[0]]] * beta)
def fit_with_hidden_status(self, visible_list, hidden_list):
"""
包含隐状态的参数估计
:param visible_list: [[],[],...,[]]
:param hidden_list: [[],[],...,[]]
:return:
"""
self.pi = np.zeros(shape=(self.hidden_status_num, 1))
self.A = np.zeros(shape=(self.hidden_status_num, self.hidden_status_num))
self.B = np.zeros(shape=(self.hidden_status_num, self.visible_status_num))
for i in range(0, len(visible_list)):
visible_status = visible_list[i]
hidden_status = hidden_list[i]
self.pi[hidden_status[0]] += 1
for j in range(0, len(hidden_status) - 1):
self.A[hidden_status[j], hidden_status[j + 1]] += 1
self.B[hidden_status[j], visible_status[j]] += 1
self.B[hidden_status[j + 1], visible_status[j + 1]] += 1
# 归一化
self.pi = self.pi / np.sum(self.pi)
self.A = self.A / np.sum(self.A, axis=0)
self.B = self.B / np.sum(self.B, axis=0)
def fit_without_hidden_status(self, visible_list=None, tol=1e-5, n_iter=10):
"""
不包含隐状态的参数估计:Baum-Welch算法
:param visible_list: [...]
:param tol:当pi,A,B的增益值变化小于tol时终止
:param n_iter:迭代次数
:return:
"""
# 初始化参数
if self.pi is None:
self.pi = np.ones(shape=(self.hidden_status_num, 1)) + np.random.random(size=(self.hidden_status_num, 1))
self.pi = self.pi / np.sum(self.pi)
if self.A is None:
self.A = np.ones(shape=(self.hidden_status_num, self.hidden_status_num)) + np.random.random(
size=(self.hidden_status_num, self.hidden_status_num))
self.A = self.A / np.sum(self.A, axis=0)
if self.B is None:
self.B = np.ones(shape=(self.hidden_status_num, self.visible_status_num)) + np.random.random(
size=(self.hidden_status_num, self.visible_status_num))
self.B = self.B / np.sum(self.B, axis=0)
for _ in range(0, n_iter):
# 计算前向概率
alphas = []
alpha = self.pi * self.B[:, [visible_list[0]]]
alphas.append(alpha)
for step in range(1, len(visible_list)):
alpha = self.A.T.dot(alpha) * self.B[:, [visible_list[step]]]
alphas.append(alpha)
# 计算后向概率
betas = []
beta = np.ones_like(self.pi)
betas.append(beta)
for step in range(len(visible_list) - 2, -1, -1):
beta = self.A.dot(self.B[:, [visible_list[step + 1]]] * beta)
betas.append(beta)
betas.reverse()
# 计算gamma值
gammas = []
for i in range(0, len(alphas)):
gammas.append((alphas[i] * betas[i])[:, 0])
gammas = np.asarray(gammas)
# 计算xi值
xi = np.zeros_like(self.A)
for i in range(0, self.hidden_status_num):
for j in range(0, self.hidden_status_num):
xi_i_j = 0.0
for t in range(0, len(visible_list) - 1):
xi_i_j += alphas[t][i][0] * self.A[i, j] * self.B[j, visible_list[t + 1]] * \
betas[t + 1][j][0]
xi[i, j] = xi_i_j
loss = 0.0 # 统计累计误差
# 更新参数
# 初始概率
for i in range(0, self.hidden_status_num):
new_pi_i = gammas[0][i]
loss += np.abs(new_pi_i - self.pi[i][0])
self.pi[i] = new_pi_i
# 隐状态转移概率
for i in range(0, self.hidden_status_num):
for j in range(0, self.hidden_status_num):
new_a_i_j = xi[i, j] / np.sum(gammas[:, i][:-1])
loss += np.abs(new_a_i_j - self.A[i, j])
self.A[i, j] = new_a_i_j
# 观测概率矩阵
for j in range(0, self.hidden_status_num):
for k in range(0, self.visible_status_num):
new_b_j_k = np.sum(gammas[:, j] * (np.asarray(visible_list) == k)) / np.sum(gammas[:, j])
loss += np.abs(new_b_j_k - self.B[j, k])
self.B[j, k] = new_b_j_k
# 归一化
self.pi = self.pi / np.sum(self.pi)
self.A = self.A / np.sum(self.A, axis=0)
self.B = self.B / np.sum(self.B, axis=0)
if loss < tol:
break
#随便造一组数据
O = [
[1, 2, 3, 0, 1, 3, 4],
[1, 2, 3],
[0, 2, 4, 2],
[4, 3, 2, 1],
[3, 1, 1, 1, 1],
[2, 1, 3, 2, 1, 3, 4]
]
I = O
# 有监督学习
hmm = HMM(hidden_status_num=5, visible_status_num=5)
hmm.fit_with_hidden_status(visible_list=O, hidden_list=I)
print(hmm.pi)
print(hmm.A)
print(hmm.B)
[[0.16666667] [0.33333333] [0.16666667] [0.16666667] [0.16666667]] [[0. 0.125 0.16666667 0. 0. ] [0. 0.375 0.33333333 0.5 0. ] [0. 0.375 0. 0.33333333 0.33333333] [1. 0.125 0.33333333 0. 0.66666667] [0. 0. 0.16666667 0.16666667 0. ]] [[1. 0. 0. 0. 0.] [0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 1. 0.] [0. 0. 0. 0. 1.]]
# 无监督学习
hmm = HMM(hidden_status_num=5, visible_status_num=5)
hmm.fit_without_hidden_status(O[0] + O[1] + O[2] + O[3] + O[4] + O[5])
print(hmm.pi)
print(hmm.A)
print(hmm.B)
[[0.50829342] [0.32216634] [0.00678242] [0.09996799] [0.06278983]] [[0.17883858 0.18538523 0.24457604 0.18546919 0.2047107 ] [0.18031489 0.22859986 0.24448691 0.16848722 0.17755413] [0.16895248 0.21542431 0.16450599 0.23683223 0.21459622] [0.19926632 0.17417557 0.19592024 0.213706 0.21671724] [0.27262773 0.19641504 0.15051082 0.19550536 0.18642172]] [[0.14183119 0.28448812 0.11769356 0.18773283 0.18558097] [0.15028341 0.25009173 0.18529553 0.16628994 0.18546453] [0.26203855 0.10616088 0.24203416 0.28671766 0.17614 ] [0.18980262 0.18713587 0.2094639 0.1681282 0.27618863] [0.25604423 0.1721234 0.24551285 0.19113137 0.17662586]]
ps:想想无监督学习的意义...,也许可以拿来作半监督学习,先让监督学习学一会儿,然后再无监督学习