一.什么是隐马尔可夫模型¶
隐马尔科夫模型(HMM)主要用于时序的概率模型,它假设由一个隐藏的马尔科夫链随机生成不可观测的隐状态序列,再由各个隐状态随机生成一个观测态从而得到可观测序列,如下图:
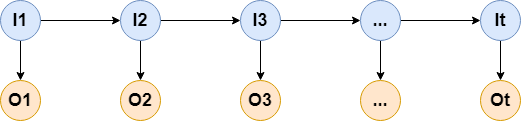
所以,HMM可以由初始概率分布,状态转移概率矩阵,观测概率矩阵确定,我们可以对其进行如下定义:
设$Q$是所有可能的状态的集合,$V$是所有可能的观测的集合:
$$ Q=\{q_1,q_2,...,q_N\},V=\{v_1,v_2,...,v_M\} $$这里,$N$是可能的状态数,$M$是可能的观测数,隐状态序列和观测序列可分别表示为:
$$ I=(i_1,i_2,...,i_T),O=(o_1,o_2,...,o_T),i_j\in Q,o_j\in V,j=1,2,..,T $$所以状态转移概率矩阵可以表示为:
$$ A=[a_{ij}]_{N\times N} $$这里,$a_{ij}=P(i_{t+1}=q_j\mid i_t=q_i),i=1,2,...,N,j=1,2,...,N$
观测概率矩阵可以定义为:
$$ B=[b_j(k)]_{N\times M} $$这里,$b_j(k)=P(o_t=v_k\mid i_t=q_j),k=1,2,..,M,j=1,2,...,N$
初始状态的概率分布,可以定义为:
$$ \pi=(\pi_i),\pi_i=P(i_1=q_i),i=1,2,...,N $$所以,HMM的参数:
$$ \lambda=(A,B,\pi) $$HMM的联合概率分布也能很容易写出来:
$$ p(o_1,o_2,...,o_T,i_1,i_2,...,i_T)=p(i_1)p(o_1\mid i_1)p(i_2\mid i_1)p(o_2\mid i_2)\cdots p(i_T\mid i_{T-1})p(o_T\mid i_T)\\ =p(i_1)p(o_1\mid i_1)\prod_{t=2}^Tp(i_t\mid i_{t-1})p(o_t\mid i_t)\\ =\pi_{i_1}b_{i_1}(o_1)\prod_{t=2}^Ta_{i_{t-1}i_t}b_{i_t}(o_t) $$二.$P(O\mid\lambda)$概率计算¶
我们通常需要处理这样的任务,给定一个隐马尔科夫模型$\lambda=(A,B,\pi)$,计算某观测序列$O=(o_1,o_2,...,o_T)$出现的概率,即$P(O\mid\lambda)$,但是隐马尔科夫模型能给我们的是联合概率分布$P(O,I\mid\lambda)$,这里$I=(i_1,i_2,...,i_T)$,所以我们需要将隐状态积分积掉:
$$ P(O\mid\lambda)=\sum_IP(O,I\mid\lambda)\\ =\sum_{i_1=1}^N\sum_{i_2=1}^N\cdots\sum_{i_T=1}^N\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)\cdots a_{i_{T-1}i_T}b_{i_T}(o_T) $$但如果直接这样暴力求解,计算的时间复杂度很高,为$O(TN^T)$,解决方案其实在马尔科夫链的计算中已经有提及了,我们可以采用动态规划的方式,将需要重复计算的结果缓存起来,我们简单分析一下,对于每个求解项,当对于$i_2,i_3,...,i_T$进行求和计算时,其实每项前面的$\pi_{i_1}b_{i_1}(o_1),i_1=q_1,q_2,...,q_N$都会被重复计算多遍,同理对于$i_3,i_4,...,i_T$进行计算时,包含$i_2,o_2$及其前面的项也会被重复计算...,所以如果在每次计算是都利用前面已经计算好的结果时,这将大大减少计算量,具体说来我们可以这样操作:
前向算法¶
首先对前向概率做定义$\alpha_t(i)=P(o_1,o_2,...,o_t,i_t=q_i\mid\lambda)$,即到时刻$t$,部分观测序列为$o_1,o_2,...,o_t$且隐状态为$q_i$的概率,接下来叙述算法流程:
$$ \alpha_1(i)=\pi_ib_i(o_1),i=1,2,...,N $$(1)计算初始值:
$$ \alpha_{t+1}=[\sum_{j=1}^N\alpha_t(j)a_{ji}]b_i(o_{t+1}),i=1,2,...,N $$(2)递推 对$t=1,2,...,T-1$,计算:
$$ P(O\mid\lambda)=\sum_{i=1}^N\alpha_T(i)) $$(3)最后:
可以发现使用动态规划后,复杂度大大降低了,只有$O(N^2T)$,由于条件独立性假设,后面的概率计算其实与前面相互独立,所以我们也可以从反方向使用动态规划
后向算法¶
首先对后向概率做定义$\beta_t(i)=P(o_{t+1},o_{t+2},...,o_T\mid i_t=q_i,\lambda)$,即在时刻$t$状态为$q_i$的条件下,从t+1到T的部分观测序列为$o_{t+1},o_{t+2},...,o_T$的概率,接下来看看求解流程:
$$ \beta_T(i)=1,i=1,2,...,N $$(1)赋初始值:
$$ \beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),i=1,2,...,N $$(2)对$t=T-1,T-2,...,1$:
$$ P(O\mid\lambda)=\sum_{i=1}^N\pi_ib_i(o_1)\beta_1(i) $$(3)最后:
前向+后向¶
其实前向和后向算法是可以同时进行的,它们互相独立计算,然后到中间任意时刻$t,t=1,2,...,T$再“会师”即可,如下图:
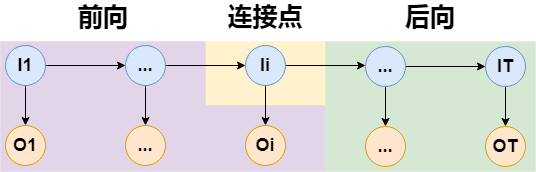
所以:
$$ P(O\mid\lambda)=\sum_{i=1}^N\alpha_t(i)\beta_t(i),t=1,2,...,T $$三.代码实现¶
"""
隐马尔科夫模型实现,封装到ml_models.pgm
"""
import numpy as np
class HMM(object):
def __init__(self, hidden_status_num=None, visible_status_num=None):
"""
:param hidden_status_num: 隐状态数
:param visible_status_num: 观测状态数
"""
self.hidden_status_num = hidden_status_num
self.visible_status_num = visible_status_num
# 定义HMM的参数
self.pi = None # 初始隐状态概率分布 shape:[hidden_status_num,1]
self.A = None # 隐状态转移概率矩阵 shape:[hidden_status_num,hidden_status_num]
self.B = None # 观测状态概率矩阵 shape:[hidden_status_num,visible_status_num]
def predict_joint_visible_prob(self, visible_list=None, forward_type="forward"):
"""
前向/后向算法计算观测序列出现的概率值
:param visible_list:
:param forward_type:forward前向,backward后向
:return:
"""
if forward_type == "forward":
# 计算初始值
alpha = self.pi * self.B[:, [visible_list[0]]]
# 递推
for step in range(1, len(visible_list)):
alpha = self.A.T.dot(alpha) * self.B[:, [visible_list[step]]]
# 求和
return np.sum(alpha)
else:
# 计算初始值
beta = np.ones_like(self.pi)
# 递推
for step in range(len(visible_list) - 2, -1, -1):
beta = self.A.dot(self.B[:, [visible_list[step + 1]]] * beta)
# 最后一步
return np.sum(self.pi * self.B[:, [visible_list[0]]] * beta)
就用李航老师的例10.2做个计算:
(1)开始,假设有3个盒子,选择每个盒子的概率分别为[0.2,0.4,0.4];
(2)然后,从当前盒子转移到下一个盒子的规则如下,即如果当前盒子是1,那么下一个继续是盒子1的概率为0.2,转移到盒子2的概率是0.2,转移到盒子3的概率是0.3,如果当前是盒子2,转移到盒子1的概率是0.3,继续留在盒子2的概率是0.5...
$$ \begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5 \end{bmatrix} $$(3)确定盒子后,从每个盒子里面抽出红球、白球的概率矩阵如下,即从盒子1抽出红球的概率为0.5,抽出白球的概率为0.5....
$$ \begin{bmatrix} 0.5 & 0.5\\ 0.4 & 0.6\\ 0.7 & 0.3 \end{bmatrix} $$目前观测到的结果为:(红,白,红),求其概率$P(O\mid\lambda)$
#造数据
pi = np.asarray([[0.2], [0.4], [0.4]])
A = np.asarray([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
B = np.asarray([[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]])
hmm = HMM()
hmm.pi = pi
hmm.A = A
hmm.B = B
#查看结果:前向
hmm.predict_joint_visible_prob([0, 1, 0],forward_type="forward")
0.130218
#查看结果:后向
hmm.predict_joint_visible_prob([0, 1, 0],forward_type="backward")
0.130218