一.难点复盘¶
这一节先跳出上一节的具体案例,对其过程做一个抽象的复盘,我们的目标是最大化一个似然函数:
$$ \theta^*=arg\max_\theta P(X\mid \theta) $$其中$\theta$为模型参数,$X$为可观测数据,但是呢,$P(X\mid\theta)$可能会比较复杂,比如上一节的多个高斯分布的情况,这时,我们可以将$P(X\mid\theta)$拆分为两部分:
$$ P(X\mid\theta)=\sum_{Z}P(Z\mid\theta)P(X\mid\theta,Z) $$这里$Z$是我们定义的一个辅助变量,它无法被直接观测到,所以称其为隐变量,比如上一节中选择第一个还是第二个高斯模型这个过程便可视为隐变量,上面的等式相当于对$P(X\mid\theta)$做了一个全概率展开(另外需要注意的是,如果$Z$是连续变量,上面的求和符号需要修改为求积分),所以痛点也来了,我们的损失函数一般是对似然函数的对数,如下:
$$ L(\theta)=logP(X\mid\theta)=log(\sum_{Z}P(Z\mid\theta)P(X\mid\theta,Z)) $$接下来,如果直接通过对参数求偏导,并令其为0进行求解将会十分困难,这便是含有隐变量的极大似然估计求解的难点
二.EM算法导出¶
EM的求解思想是寻找一个参数序列,它们能使得似然估计值逐步提升,即:
$$ \theta^1->\theta^2->,...,->\theta^i\Rightarrow L(\theta^1)<L(\theta^2)<\cdots<L(\theta^i) $$假如,当前轮为第$i$轮,当前的参数为$\theta^i$,那么下一步即是在此基础上找到一个$\theta^{i+1}$使得$L(\theta^{i+1})>L(\theta^i)$;
按照条件概率公式,我们可以对$P(X\mid\theta)$做如下变换:
$$ P(X\mid\theta)=\frac{P(X,Z\mid\theta)}{P(Z\mid X,\theta)} $$所以:
$$ L(\theta)=logP(X\mid\theta)=logP(X,Z\mid\theta)-logP(Z\mid X,\theta) $$那么,如何用到上一步$\theta^i$的信息呢?既然上一步学到了$\theta^i$,那么我们可以在此基础上求得一个关于的$Z$的分布,即$P(Z\mid X,\theta^i)$,所以,我们可以求$L(\theta)$在分布$P(Z\mid X,\theta^i)$上的期望:
$$ \sum_{Z}logP(X\mid\theta)P(Z\mid X,\theta^i)=\sum_{Z}logP(X,Z\mid\theta)P(Z\mid X,\theta^i)-\sum_{Z}logP(Z\mid X,\theta)P(Z\mid X,\theta^i)\\ \Rightarrow logP(X\mid\theta)=\sum_{Z}logP(X,Z\mid\theta)P(Z\mid X,\theta^i)-\sum_{Z}logP(Z\mid X,\theta)P(Z\mid X,\theta^i)\\ \Rightarrow L(\theta)=\sum_{Z}logP(X,Z\mid\theta)P(Z\mid X,\theta^i)-\sum_{Z}logP(Z\mid X,\theta)P(Z\mid X,\theta^i)\\ \Rightarrow L(\theta)=Q(\theta,\theta^i)-H(\theta,\theta^i) $$说一下,第一步变换,由于$P(X\mid\theta)$本身与$Z$无关($Z$是我们为了方便求解而添加的变量),所以:
$$ \sum_{Z}logP(X\mid\theta)P(Z\mid X,\theta^i)=logP(X\mid\theta)\sum_{Z}P(Z\mid X,\theta^i)=logP(X\mid\theta) $$最后一步是令:
$$ Q(\theta,\theta^i)=\sum_{Z}logP(X,Z\mid\theta)P(Z\mid X,\theta^i)\\ H(\theta,\theta^i)=\sum_{Z}logP(Z\mid X,\theta)P(Z\mid X,\theta^i) $$另外一点需要注意的是$\theta$是未知量,$\theta^i$是已知量,到这一步,我们已经能看到下一步优化的方向了,即:
$$ \theta^{i+1}=arg\max_\theta Q(\theta,\theta^i)-H(\theta,\theta^i) $$但实际求解时只对$Q$函数做极大值求解:
$$ \theta^{i+1}=arg\max_\theta Q(\theta,\theta^i) $$这是因为,对$H$函数一定有$H(\theta^{i+1},\theta^i)\leq H(\theta^i,\theta^i)$,所以必然能满足$L(\theta^{i+1})\geq L(\theta^i)$,下面对其做证明
三.EM收敛性证明¶
EM的收敛性证明包括两部分,第一部分是$L(\theta)$的收敛性,另一部分是$\theta$的收敛性
$L(\theta)$的收敛性¶
关于$L(\theta)$的收敛性还差上面的$H(\theta^{i+1},\theta^i)\leq H(\theta^i,\theta^i)$没有证明,因为通过$\theta^{i+1}=arg\max_\theta Q(\theta,\theta^i)$的求解,必然有$Q(\theta^{i+1},\theta^i)\geq Q(\theta^i,\theta^i)$,下面对其证明:
$$ H(\theta^{i+1},\theta^i) - H(\theta^i,\theta^i)=\sum_{Z}(log\frac{P(Z\mid X,\theta^{i+1})}{P(Z\mid X,\theta^i)})P(Z\mid X,\theta^i)\\ \leq log(\sum_Z\frac{P(Z\mid X,\theta^{i+1})}{P(Z\mid X,\theta^i)}P(Z\mid X,\theta^i))\\ =log(\sum_Z P(Z\mid X,\theta^i))=log 1=0 $$关于第一个不等式,其实用到了Jensen不等式,这可以由凹函数的定义得到,若$f(x)$为凹函数,则$\forall \alpha_1,\alpha_2,...,\alpha_n>0,\sum_{i=1}^n\alpha_i=1,\forall x_i,i=1,2,..,n$,有:
$$ f(\sum_{i=1}^n x_i)\geq \sum_{i=1}^n\alpha_if(x_i) $$而$log(x)$为凹函数,将上面的$x_j$视作$\frac{P(Z_j\mid X,\theta^{i+1})}{P(Z_j\mid X,\theta^i)}$,$\alpha_j$视作$P(Z_j\mid X,\theta^i)$即可得证,至于凹函数为什么会有这样的性质,就简单画图说明一下,如下,我们在$log(x)$上任意取了两点$x_1,x_2$,它对应的函数值为$log(x_1),log(x_2)$,红色实线即为$(x_1,log(x_1))$与$(x_2,log(x_2))$之间的连线,对任意的$\alpha_1+\alpha_2=1,\alpha_1,\alpha_2>0$假如其组合为$x_i=\alpha_1x_1+\alpha_2x_2$,对其做垂线,与上面的两条线分别相交,与红色实线的交点为$(x_i,\alpha_1log(x_1)+\alpha_2log(x_2))$,与$log(x)$线的交点为$(x_i,log(\alpha_1x_1+\alpha_2x_2))$,从图上结果可以看出$log(\alpha_1x_1+\alpha_2x_2)\geq \alpha_1log(x_1)+\alpha_2log(x_2)$
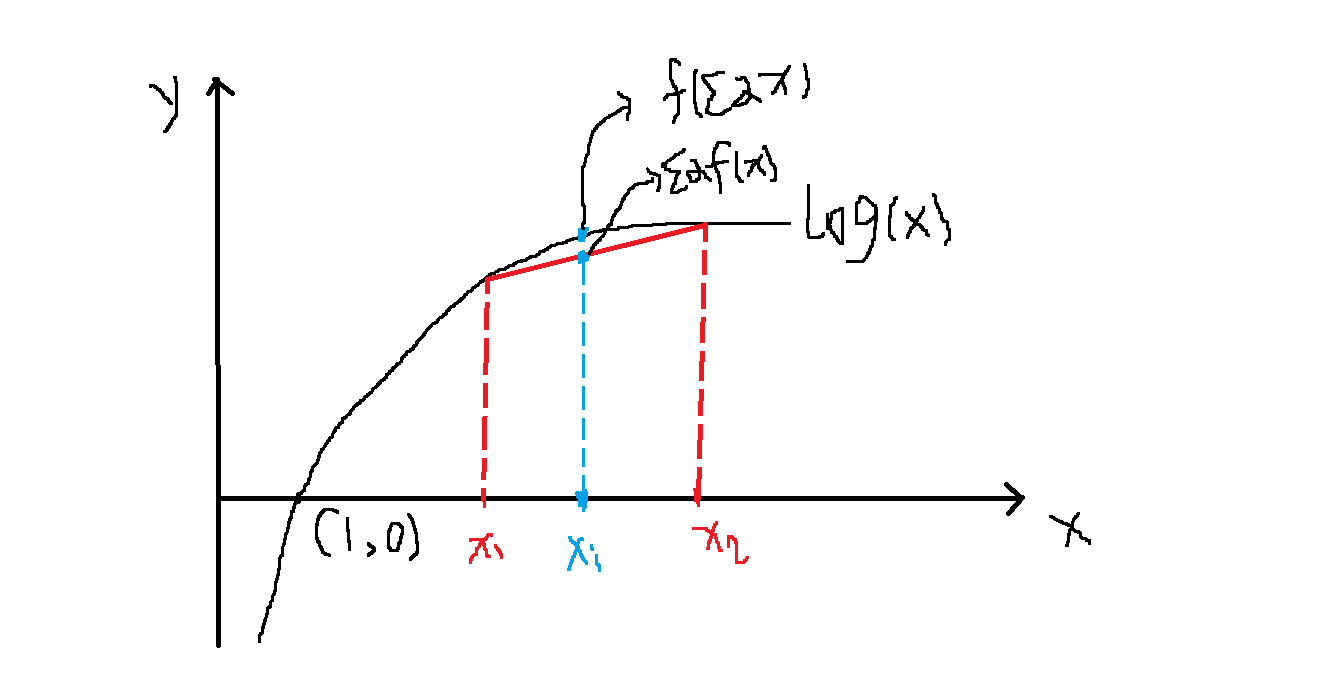 到这一步,我们已经证明了$L(\theta^{i+1})\geq L(\theta^i)$,由于$L(\theta)=P(X\mid \theta)$,而$P(X\mid\theta)\leq1$,所以$L(\theta)$有上界,收敛性得证
到这一步,我们已经证明了$L(\theta^{i+1})\geq L(\theta^i)$,由于$L(\theta)=P(X\mid \theta)$,而$P(X\mid\theta)\leq1$,所以$L(\theta)$有上界,收敛性得证
$\theta$的收敛性证明¶
关于这部分就不证明了,直接说下文献《On the Convergence Properties of the EM Algorithm》的证明结论:大部分情况下,$\theta$是收敛的,且收敛于$L(\theta)$的稳定点
四.防坑指南¶
(1)算法层面:EM算法只能保证收敛到稳定点,这个点可能会是鞍点;
(2)损失函数层面:$L(\theta)$不一定保证是凹函数,所以EM算法不一定能收敛到最优的解
解决方法:多试几组初始参数...