一.模型的特征重要性¶
以xgboost为例,说明模型特征重要性的几种计算方式,
(1)importance_type=weight(默认值):特征在所有树中作为划分属性的次数;
(2)importance_type=gain: 特征在作为划分属性时loss平均的降低量,以特征$k=1,2,...,K$为例,其重要度计算可以表述如下:
$$ V(k)=\frac{1}{2}\frac{\sum_{t=1}^T\sum_{i=1}^{N(t)}I(\beta(t,i)=k)(\frac{G_{\gamma(t,i,L)}^2}{H_{\gamma(t,i,L)}^2+\lambda}+\frac{G_{\gamma(t,i,R)}^2}{H_{\gamma(t,i,R)}^2+\lambda}-\frac{G_{\gamma(t,i)}^2}{H_{\gamma(t,i)}^2+\lambda})}{\sum_{t=1}^T\sum_{i=1}^{N(t)}I(\beta(t,i)=k)} $$这里$k$表示某节点,$T$表示所有树的数量,$N(t)$表示第$t$颗树的非叶子节点数量,$\beta(t,i)$表示第$t$颗树的第$i$个非叶节点的划分特征,所以$\beta(\cdot)\in \{1,2,...,K\}$,$I(\cdot)$是指示函数,$G_{\gamma(t,i)}$、$H_{\gamma(t,i)}$分别表示落在第$t$颗树的第$i$个非叶节点上所有样本的一阶导数和二阶导数之和,$G_{\gamma(t,i,L)},G_{\gamma(t,i,R)}$分别表示落在第$t$颗树上第$i$个非叶节点的左、右节点上的一阶导数之和,同理$H_{\gamma(t,i,L)},H_{\gamma(t,i,R)}$表示落在第$t$颗树上第$i$个非叶节点的左、右节点上的二阶导数之和,所以有$G_{\gamma(t,i)}=G_{\gamma(t,i,L)}+G_{\gamma(t,i,R)}$,$H_{\gamma(t,i)}=H_{\gamma(t,i,L)}+H_{\gamma(t,i,R)}$ ,$\lambda$为正则化项的超参数
(3)importance_type=cover:特征在作为划分属性时对应样本的二阶导数之和的平均值:
$$ V(k)=\frac{\sum_{t=1}^T\sum_{i=1}^{N(t)}I(\beta(t,i)=k)H_{\gamma(t,i)}}{\sum_{t=1}^T\sum_{i=1}^{N(t)}I(\beta(t,i)=k)} $$
这里各符号的意义与上面相同,另外需要注意的一点是,当损失函数是平方损失时,$H_{\gamma(t,i)}$刚好表示落到第$t$颗树的第$i$个节点上的样本量(每个样本的二阶导数为1),这时cover指标即是样本的平均覆盖量
二.样本的特征重要性¶
接下来介绍样本的特征重要性,前面介绍的几种方式只能对模型的特征重要度做整体评估,无法实现样本的个性化评估,在某些场景下,我们需要计算样本的各特征对预测结果的贡献,从而可以对预测结果进行解释,Saabas和SHAP就是比较典型的两种方式
Saabas¶
Saabas的思路很清晰,对于一颗决策树,每个样本的预测值是由根节点到叶子节点路径上的一系列决策共同决定的,路径上的每个特征均会对该样本的最终预测值产生影响,而路径上每个特征的贡献值可以通过路径下一个节点的值减去本节点的值得到。那么节点的值如何计算呢?
(1)对于叶子节点,其值就是它的预测值;
(2)对于非叶子节点,其值是它的子节点的加权平均,权重为子节点包含的cover值/样本数做归一化;
如下示例,假如各个叶子节点的cover值一样,那么,各个节点的值如下:
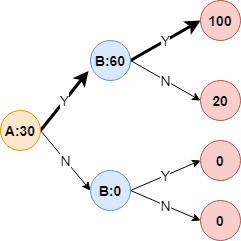
假如预测路径为黑体的线,那么预测结果可拆解为:
$$ predict=30+(60-30)+(100-60)=30(基础分)+30(特征A的贡献值)+40(特征B的贡献值)=100 $$可以发现Saabas天然具有很好的加和性质,我们可以将上述过程抽象为如下数学表达式:
$$ f(x)=b+\sum_{k=1}^KC(x,k) $$$b$为基础分,$K$为特征数量,$C(x,k)$表示对于样本$x$的第$k$个特征的贡献值(注意,如果同一特征在路径上被多次选择,则$C(x,k)$表示它们之和),上面的计算结果有些“反直觉”的地方,考虑如下几个情景:
(1)A=Y,B=Y的情况下,输出值为100;
(2)A=Y,B=N的情况下,输出值为20;
(3)A=N,B=Y的情况下,输出值为0;
从(2),(3)可以感受出,当A=Y时要比B=Y时的贡献更大(20->0),但是看(1)中,A的贡献值(30)却要比B的贡献值(40)更低,下面的SHAP具有更好的性质,可以解决这个问题
SHAP¶
定义如下,计算样本的第$j$个特征重要度的公式:
$$ \phi_j(val)=\sum_{S\subseteq \{x_1,x_2,...,x_p\}/ \{x_j\}}\frac{|S|!(p-|S|-1)!}{p!}(val(S\cup\{x_j\})-val(S)) $$$S$是特征子集,$x$是样本特征值,$val_x(S)$是针对集合S特征值的预测,$p$是总的特征数;
1. $val(S)$的计算¶
接下来用一个小案例介绍如何在树中计算SHAP值,其实最关键的就是$val(S)$的计算,同上面的例子,假如只有一颗树,特征只有$A,B$,其构成的树如下,且对$A,B$的预测结果也为右上角叶子节点值为100的那个点,假如要计算$S=\{A\}$ 的$val(S)$值:
(1)首先初始化权重$w=1$
(2)当前根节点的切分特征为$A$,由于$A\in S$,则移动到下一个节点(上方的$B$)
(3)由于当前的节点$B\notin S$,所以要对$w$按左右子树的样本量/cover值分权,假如左右样本量相等,则左子树$w=0.5$,右边子树$w=0.5$
(4)最后计算叶子节点的加权求和值$val(S)=0.5*100+0.5*20=60$

按照同样的思路,可以计算出$val(\{\})=30,val(\{B\})=50,val(\{A,B\})=100$
小节一下,主要就是对为空的那部分特征按照cover值分权
2. $\phi(\cdot)$的计算¶
接下来就是套上面的公式计算就是了,$S$一共有2种取值情况,以及其对应的阶乘值如下:
(1)$S=\{\}$:$|S|!=1,p=2$;
(2)$S=\{B\}$:$|S|!=1,p=2$;
所以$\phi_A=\frac{1}{2}(val(\{A\}-val(\{\})))+\frac{1}{2}(val(\{A,B\}-val(\{B\})))=40$,同样的思路可以计算出$\phi_B=30$,这里$\phi_A>\phi_B$,解决了Saabas的不足;而且SHAP同样满足加和性质:$\phi_0+\phi_A+\phi_B=100$,$\phi_0=val(\{\})=30$,另外Shap算法已经调通并放在了ml_models.explain.shap.py中,对应测试代码在ml_models.tests.shap_test.py中,就不贴到下面了
Tree Shap¶
但是呢,如果直接采用Shap的方式计算因子权重,复杂度会很高,对于特征数为$p$的情况,会产生$2^p$个子集,这意味着计算的时间复杂度会随着特征数指数级增加,而一种优化想法便是在一轮迭代时计算所有子集的情况,比如对上方的$val(\{\}),val(\{A\}),val(\{B\}),val(\{A,B\})$同时计算,而不是分别计算,因为它们可以共享同一个迭代过程,我们以上面$\phi(A)$为例,对其计算过程进行拆解:
$$
\phi_A=\frac{1}{2}(val(\{A\}-val(\{\})))+\frac{1}{2}(val(\{A,B\}-val(\{B\})))\\
=([\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}]*[-1,1,-1,1])@[val(\{\}),val(\{A\}),val(\{B\}),val(\{A,B\})]^T
$$
其中,$*$表示按元素相乘,$@$表示矩阵乘法,
(1)这里第一个矩阵中的$\frac{1}{2}$便是对应的$\frac{|S|!(p-|S|-1)!}{p!}$系数(碰巧这里都一样了,另外需要注意的是$|S|$对于如果是包含了当前特征的情况,需要减掉1,比如对于子集$\{A,B\}$,只算$\{B\}$的大小);
(2)第二个矩阵中的$1$表示目标特征在当前子集中,而$-1$表示目标特征不在当前子集中;
(3)第三个矩阵便是对应的子集的$val(\cdot)$取值,而对于$val(\cdot)$,我们还可以进一步拆解,由上面Shap这一段的推导,我们知道$val(\cdot)$可以表示为叶子节点的加权线性组合,而且权重之和为1,比如:
$$ val(\{A\})=[0.5,0.5,0,0]@[100,20,0,0]^T $$其中,$[100,20,0,0]$即是对应的叶节点取值(上图从上到下),而$[0.5,0.5,0,0]$即是对应的权重,同样的另外几个,我们也可以表示出来了:
$$ val(\{\})=[0.25,0.25,0.25,0.25]@[100,20,0,0]^T\\ val(\{B\})=[0.5,0,0.25,0.25]@[100,20,0,0]^T\\ val(\{A,B\})=[1,0,0,0]@[100,20,0,0]^T\\ $$所以,$\phi(A)$可以表示为如下几项的计算:
$$ \phi_A=([\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}]*[-1,1,-1,1])@\begin{bmatrix} 0.25 & 0.25 & 0.25 & 0.25\\ 0.5 & 0.5 & 0 & 0\\ 0.5 & 0 & 0.25 & 0.25\\ 1 & 0 & 0 & 0 \end{bmatrix}@[100,20,0,0]^T $$按照相同的处理,我们可以得到:
$$ \phi_0=([1,0,0,0]*[1,0,0,0])@\begin{bmatrix} 0.25 & 0.25 & 0.25 & 0.25\\ 0.5 & 0.5 & 0 & 0\\ 0.5 & 0 & 0.25 & 0.25\\ 1 & 0 & 0 & 0 \end{bmatrix}@[100,20,0,0]^T\\ $$$$ \phi_B=([\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}]*[-1,-1,1,1])@\begin{bmatrix} 0.25 & 0.25 & 0.25 & 0.25\\ 0.5 & 0.5 & 0 & 0\\ 0.5 & 0 & 0.25 & 0.25\\ 1 & 0 & 0 & 0 \end{bmatrix}@[100,20,0,0]^T $$这里,对于$\phi_0$的处理特殊一点,它的第二个矩阵每个元素之和不要求等于0,现在我们将这些计算合并起来,我们令:
$$ \phi=[\phi_0,\phi_A,\phi_B]^T $$那么:
$$ \phi=\left (\begin{bmatrix} 1 & 0 & 0 & 0\\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix}*\begin{bmatrix} 1 & 0 & 0 & 0\\ -1 & 1 & -1 & 1\\ -1 & -1 & 1 & 1 \end{bmatrix}\right )@\begin{bmatrix} 0.25 & 0.25 & 0.25 & 0.25\\ 0.5 & 0.5 & 0 & 0\\ 0.5 & 0 & 0.25 & 0.25\\ 1 & 0 & 0 & 0 \end{bmatrix}@[100,20,0,0]^T $$我们将上面的四个矩阵可以依次表示为:
$$ \phi=(L*S)@W@V^T $$接下来,我们再挨个看下这几个矩阵计算逻辑(下面的符号表达不够严谨,明白意思就好~~~)
(1)$L(i,j)$矩阵表示各个$\phi_i$在子集合$j$上的系数$\frac{|S|!(p-|S|-1)!}{p!}$,所以这个矩阵无需对树进行遍历,可以预计算好;
(2)$S(i,j)$矩阵表示各个特征$(i)$是否出现在子集合$j$中,如果出现则为$1$,否则为$-1$($\phi_0$除外),这个操作也可以预先算好;
(3)$W_{i,j}$即是我们上面Shap案例所作的操作,即将权重$w_i=1$分到各个叶子节点$j$上的份额,这个操作在树的递归阶段完成;
(4)而$V$即是我们已知的叶子节点取值
而Tree Shap算法便是通过迭代树的过程将$W$计算出来,其关键流程同Shap的计算一样,但同时将$L$和$S$矩阵的权重加入到计算中,遗憾是笔者对于论文《Consistent feature attribution for tree ensembles》中的Tree Shap代码还没debug正确,哈哈哈~~~ ,对应代码同样放在了ml_models.explain.shap.py中,对应测试代码也在ml_models.tests.shap_test.py中,感兴趣的同学可以继续debug