一.利用回归树实现分类¶
分类也可以用回归树来做,简单说来就是训练与类别数相同的几组回归树,每一组代表一个类别,然后对所有组的输出进行softmax操作将其转换为概率分布,然后再通过交叉熵或者KL一类的损失函数求每颗树相应的负梯度,指导下一轮的训练,以三分类为例,流程如下:
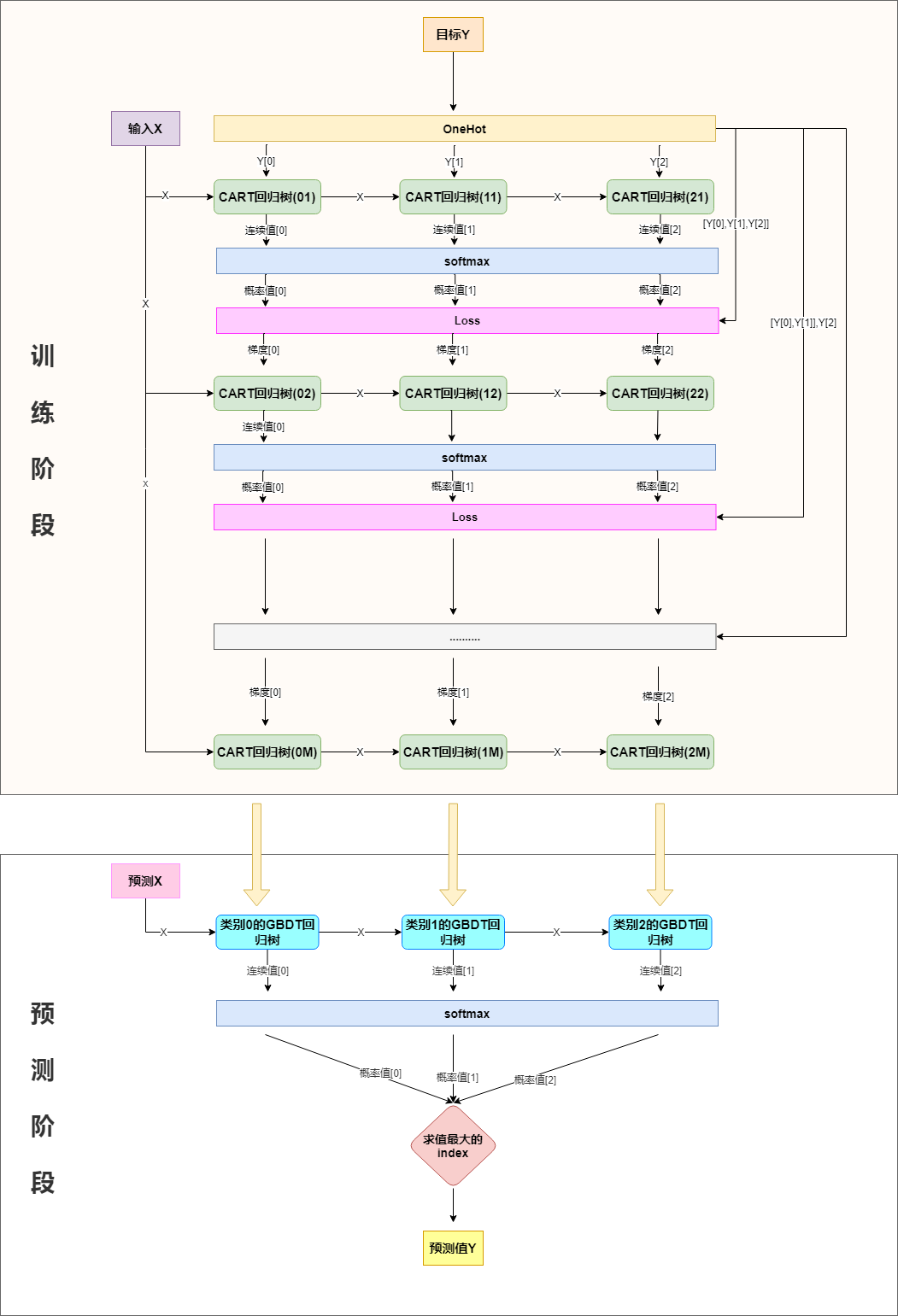
二.softmax+交叉熵损失,及其梯度求解¶
分类问题,一般会选择用交叉熵作为损失函数,下面对softmax+交叉熵损失函数的梯度做推导:
softmax函数在最大熵那一节已有使用,再回顾一下:
$$ softmax([y_1^{hat},y_2^{hat},...,y_n^{hat}])=\frac{1}{\sum_{i=1}^n e^{y_i^{hat}}}[e^{y_1^{hat}},e^{y_2^{hat}},...,e^{y_n^{hat}}] $$交叉熵在logistic回归有介绍:
$$ cross\_entropy(y,p)=-\sum_{i=1}^n y_ilog p_i $$将$p_i$替换为$\frac{e^{y_i^{hat}}}{\sum_{i=1}^n e^{y_i^{hat}}}$即是我们的损失函数:
$$ L(y^{hat},y)=-\sum_{i=1}^n y_ilog \frac{e^{y_i^{hat}}}{\sum_{j=1}^n e^{x_j^{hat}}}\\ =-\sum_{i=1}^n y_i(y_i^{hat}-log\sum_{j=1}^n e^{y_j^{hat}})\\ =log\sum_{i=1}^n e^{y_i^{hat}}-\sum_{i=1}^ny_iy_i^{hat}(由于是onehot展开,所以\sum_{i=1}^n y_i=1) $$计算梯度:
$$ \frac{\partial L(y^{hat},y)}{\partial y^{hat}}=softmax([y_1^{hat},y_2^{hat},...,y_n^{hat}])-[y_1,y_2,...,y_n] $$所以,第一组回归树的拟合目标为$y_1-\frac{e^{y_1^{hat}}}{\sum_{i=1}^n e^{y_i^{hat}}}$,第二组回归树学习的拟合目标为$y_2-\frac{e^{y_2^{hat}}}{\sum_{i=1}^n e^{y_i^{hat}}}$,....,第$n$组回归树的拟合目标为$y_n-\frac{e^{y_n^{hat}}}{\sum_{i=1}^n e^{y_i^{hat}}}$
三.代码实现¶
In [1]:
import os
os.chdir('../')
from ml_models.tree import CARTRegressor
from ml_models import utils
import copy
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
class GradientBoostingClassifier(object):
def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0):
"""
:param base_estimator: 基学习器,允许异质;异质的情况下使用列表传入比如[estimator1,estimator2,...,estimator10],这时n_estimators会失效;
同质的情况,单个estimator会被copy成n_estimators份
:param n_estimators: 基学习器迭代数量
:param learning_rate: 学习率,降低后续基学习器的权重,避免过拟合
"""
self.base_estimator = base_estimator
self.n_estimators = n_estimators
self.learning_rate = learning_rate
if self.base_estimator is None:
# 默认使用决策树桩
self.base_estimator = CARTRegressor(max_depth=2)
# 同质分类器
if type(base_estimator) != list:
estimator = self.base_estimator
self.base_estimator = [copy.deepcopy(estimator) for _ in range(0, self.n_estimators)]
# 异质分类器
else:
self.n_estimators = len(self.base_estimator)
# 扩展class_num组分类器
self.expand_base_estimators = []
def fit(self, x, y):
# 将y转one-hot编码
class_num = np.amax(y) + 1
y_cate = np.zeros(shape=(len(y), class_num))
y_cate[np.arange(len(y)), y] = 1
# 扩展分类器
self.expand_base_estimators = [copy.deepcopy(self.base_estimator) for _ in range(class_num)]
# 拟合第一个模型
y_pred_score_ = []
# TODO:并行优化
for class_index in range(0, class_num):
self.expand_base_estimators[class_index][0].fit(x, y_cate[:, class_index])
y_pred_score_.append(self.expand_base_estimators[class_index][0].predict(x))
y_pred_score_ = np.c_[y_pred_score_].T
# 计算负梯度
new_y = y_cate - utils.softmax(y_pred_score_)
# 训练后续模型
for index in range(1, self.n_estimators):
y_pred_score = []
for class_index in range(0, class_num):
self.expand_base_estimators[class_index][index].fit(x, new_y[:, class_index])
y_pred_score.append(self.expand_base_estimators[class_index][index].predict(x))
y_pred_score_ += np.c_[y_pred_score].T * self.learning_rate
new_y = y_cate - utils.softmax(y_pred_score_)
def predict_proba(self, x):
# TODO:并行优化
y_pred_score = []
for class_index in range(0, len(self.expand_base_estimators)):
estimator_of_index = self.expand_base_estimators[class_index]
y_pred_score.append(
np.sum(
[estimator_of_index[0].predict(x)] +
[self.learning_rate * estimator_of_index[i].predict(x) for i in
range(1, self.n_estimators - 1)] +
[estimator_of_index[self.n_estimators - 1].predict(x)]
, axis=0)
)
return utils.softmax(np.c_[y_pred_score].T)
def predict(self, x):
return np.argmax(self.predict_proba(x), axis=1)
In [2]:
#造伪数据
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
In [3]:
# 同质
classifier = GradientBoostingClassifier(base_estimator=CARTRegressor(),n_estimators=10)
classifier.fit(data, target)
utils.plot_decision_function(data, target, classifier)
In [4]:
#异质
from ml_models.linear_model import LinearRegression
classifier = GradientBoostingClassifier(base_estimator=[LinearRegression(),LinearRegression(),LinearRegression(),CARTRegressor(max_depth=2)])
classifier.fit(data, target)
utils.plot_decision_function(data, target, classifier)
In [ ]: