二.算法流程¶
输入:训练集$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$,其中$x_i\in R^n,y_i\in\{+1,-1\},i=1,2,...,N$
输出:最终分类器$G(x)$
$$ D_1=(w_{11},...,w_{1i},...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N $$(1)初始化训练数据的权重分布:
(2)对$m=1,2,...,M:$
$$ w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-\alpha_my_iG_m(x_i)),i=1,2,...,N $$(2.1)使用具有权重分布$D_m$的训练数据集学习,得到基本分类器:$G_m(x)$
(2.2)计算$G_m(x)$在训练集上的分类误差率:$e_m=\sum_{i=1}^NP(G_m(x_i)\neq y_i)=\sum_{i=1}^Nw_{mi}I(G_m(x_i)\neq y_i)$
(2.3)计算$G_m(x)$的权重系数:$\alpha_m=\frac{1}{2}ln\frac{1-e_m}{e_m}$
(2.4)更新训练样本权重:
这里$Z_m$是归一化因子
$$ G(x)=sign(\sum_{m=1}^M\alpha_mG_m(x)) $$(3)基于基分类器,构建最终的分类器:
简单来说大致流程如下:
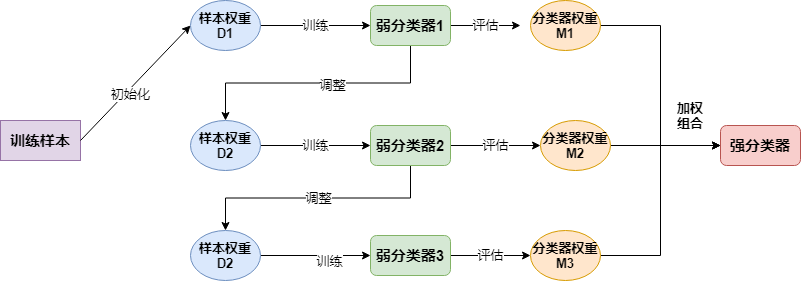
三.代码实现¶
import os
os.chdir('../')
from ml_models import utils
from ml_models.tree import CARTClassifier
import copy
import numpy as np
%matplotlib inline
"""
AdaBoost分类器的实现,封装到ml_models.ensemble
"""
class AdaBoostClassifier(object):
def __init__(self, base_estimator=None, n_estimators=10, learning_rate=1.0):
"""
:param base_estimator: 基分类器,允许异质;异质的情况下使用列表传入比如[estimator1,estimator2,...,estimator10],这时n_estimators会失效;
同质的情况,单个estimator会被copy成n_estimators份
:param n_estimators: 基分类器迭代数量
:param learning_rate: 学习率,降低后续基分类器的权重,避免过拟合
"""
self.base_estimator = base_estimator
self.n_estimators = n_estimators
self.learning_rate = learning_rate
if self.base_estimator is None:
# 默认使用决策树桩
self.base_estimator = CARTClassifier(max_depth=2)
# 同质分类器
if type(base_estimator) != list:
estimator = self.base_estimator
self.base_estimator = [copy.deepcopy(estimator) for _ in range(0, self.n_estimators)]
# 异质分类器
else:
self.n_estimators = len(self.base_estimator)
# 记录estimator权重
self.estimator_weights = []
def fit(self, x, y):
n_sample = x.shape[0]
sample_weights = np.asarray([1.0] * n_sample)
for index in range(0, self.n_estimators):
self.base_estimator[index].fit(x, y, sample_weight=sample_weights)
indicates = (self.base_estimator[index].predict(x) == y).astype(int)
# 计算误分率
error_rate = np.sum([sample_weights[j] * (1.0 - indicates[j]) for j in range(0, n_sample)]) / n_sample
# 计算权重系数
alpha_rate = 1.0 / 2.0 * np.log((1 - error_rate) / (error_rate + 1e-7))
alpha_rate = min(10.0, alpha_rate)
self.estimator_weights.append(alpha_rate)
# 更新样本权重
for j in range(0, n_sample):
sample_weights[j] = sample_weights[j] * np.exp(-1.0 * alpha_rate * np.power(-1.0, 1 - indicates[j]))
sample_weights = sample_weights / np.sum(sample_weights) * n_sample
# 更新estimator权重
for i in range(0, self.n_estimators):
self.estimator_weights[i] *= np.power(self.learning_rate, i)
def predict_proba(self, x):
# TODO:并行优化
result = np.sum(
[self.base_estimator[j].predict_proba(x) * self.estimator_weights[j] for j in
range(0, self.n_estimators)],
axis=0)
return result / result.sum(axis=1, keepdims=True)
def predict(self, x):
return np.argmax(self.predict_proba(x), axis=1)
#造伪数据
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
# 同质
classifier = AdaBoostClassifier(base_estimator=CARTClassifier(max_depth=2),n_estimators=10)
classifier.fit(data, target)
utils.plot_decision_function(data, target, classifier)
#异质
from ml_models.linear_model import LogisticRegression
from ml_models.svm import SVC
classifier = AdaBoostClassifier(base_estimator=[LogisticRegression(),SVC(kernel='rbf',C=5.0),CARTClassifier()])
classifier.fit(data, target)
utils.plot_decision_function(data, target, classifier)
# 权重衰减
classifier = AdaBoostClassifier(base_estimator=[LogisticRegression(),SVC(kernel='rbf',C=5.0),CARTClassifier()],learning_rate=0.5)
classifier.fit(data, target)
utils.plot_decision_function(data, target, classifier)
四.问题讨论¶
1.基本要求:弱可学习¶
注意有个基本要求,那就是$e_m<0.5$,即分类器至少是弱可学习的,这样才能保证$\alpha_m>0$,此时样本的权重调整(如下公式)才有意义,即正确分类的样本权重降低,错误分类的样本权重升高:
$$ w_{m+1,i}=\left\{\begin{matrix} \frac{w_{mi}}{Z_m}e^{-\alpha_m}, & G_m(x_i)= y_i \\ \frac{w_{mi}}{Z_m}e^{\alpha_m} & G_m(x_i)\neq y_i \end{matrix}\right. $$对于二分类问题,弱可学习其实是很容易保证的,对于$e_m>0.5$的情况,只需要对其预测取反,即可得到$1-e_m<0.5$的错误率
2.基分类器不支持样本权重怎么办?¶
对于不能支持样本权重训练的基分类器,可以通过样本重采样来实现
五.训练误差分析¶
这一部分证明训练误差会随着基分类器的数量增加而指数下降,首先抛出第一个不等式关系:
$$ 关系式1:\frac{1}{N}\sum_{i=1}^NI(G(x_i)\neq y_i)\leq \frac{1}{N}\sum_{i=1}^Nexp(-y_if(x_i))=\prod_{m=1}^MZ_m $$这里$f(x)=\sum_{m=1}^M\alpha_mG_m(x),G(x)=sign(f(x)),Z_m$与上面的定义一样,前半部分很好证明:如果$G(x_i)\neq y_i$,则$y_if(x_i)<0$,所以$exp(-y_if(x_i))\geq 1=I(G(x_i)\neq y_i)$,而对于$G(x_i)= y_i$的情况,显然有$exp(-y_if(x_i))\geq 0=I(G(x_i\neq y_i))$;
接下来证明后半部分,根据之前的推导,有如下的两点条件需要注意:
$$ 条件1:w_{1i}=\frac{1}{N},i=1,2,...,N\\ 条件2:w_{mi}exp(-\alpha_my_iG_m(x_i))=Z_mw_{m+1,i},i=1,2,...,N,m=1,2,...,M $$所以:
$$ \frac{1}{N}\sum_{i=1}^Nexp(-y_if(x_i))\\ =\frac{1}{N}\sum_{i=1}^Nexp(-\sum_{m=1}^M\alpha_my_iG_m(x_i)))\\ =\sum_{i=1}^N \frac{1}{N}\prod_{m=1}^Mexp(-\alpha_my_iG_m(x_i))\\ =\sum_{i=1}^N w_{1i}\prod_{m=1}^Mexp(-\alpha_my_iG_m(x_i))(用到了条件1)\\ =\sum_{i=1}^N w_{1i}exp(-\alpha_1y_iG_1(x_i))\prod_{m=2}^Mexp(-\alpha_my_iG_m(x_i))\\ =\sum_{i=1}^N Z_1w_{2i}\prod_{m=2}^Mexp(-\alpha_my_iG_m(x_i))(用到了条件2)\\ =Z_1\sum_{i=1}^N w_{2i}\prod_{m=2}^Mexp(-\alpha_my_iG_m(x_i))\\ =Z_1Z_2\sum_{i=1}^N w_{3i}\prod_{m=3}^Mexp(-\alpha_my_iG_m(x_i))\\ =\cdots\\ =\prod_{m=1}^MZ_m $$接下来要抛出第二个关系式,对于二分类问题有如下不等式成立:
$$ 关系式2:\prod_{m=1}^MZ_m=\prod_{m=1}^M[2\sqrt{e_m(1-e_m)}]=\prod_{m=1}^M\sqrt{1-4\gamma_m^2}\leq exp(-2\sum_{i=1}^M\gamma_m^2) $$这里:$\gamma_m=\frac{1}{2}-e_m$,首先证明等式部分,由前面的算法部分,我们知道$e_m=\sum_{i=1}^Nw_{mi}I(G_m(x_i)\neq y_i)$,所以:
$$ Z_m=\sum_{i=1}^Nw_{mi}exp(-\alpha_my_iG_m(x_i))\\ =\sum_{y_i=G_m(x_i)}w_{mi}e^{-\alpha_m}+\sum_{y_i\neq G_m(x_i)}w_{mi}e^{\alpha_m}\\ =(1-e_m)e^{-\alpha_m}+e_me^{\alpha_m}\\ =2\sqrt{e_m(1-e_m)}\\ =\sqrt{1-4\gamma_m^2} $$至于不等式部分,其实对于$\forall 0\leq x\leq 1$,都有$e^{-x/2}\geq \sqrt{1-x}$恒成立(证明从略,直观理解如下图),将$x$替换为$4\gamma_m^2$即可得到上面的不等式,从而关系式2得到证明;
接下来简单做一个推论:一定能找到一个$\gamma>0$,对所有$\gamma_m\geq\gamma$成立,则有如下关系:
$$ 关系式3:exp(-2\sum_{i=1}^M\gamma_m^2)\leq exp(-2M\gamma^2) $$结合关系式1、2、3可以得出:
$$ \frac{1}{N}\sum_{i=1}^NI(G(x_i)\neq y_i)\leq exp(-2M\gamma^2) $$即adaboost的误差上界会随着$M$的增加以指数速率下降
import matplotlib.pyplot as plt
x=np.linspace(0,1,10)
plt.plot(x,np.sqrt(1-x),'b')
plt.plot(x,np.exp(-0.5*x),'r')
[<matplotlib.lines.Line2D at 0x21a6b0c1048>]