一.简介¶
支持向量机(svm)的想法与前面介绍的感知机模型类似,找一个超平面将正负样本分开,但svm的想法要更深入了一步,它要求正负样本中离超平面最近的点的距离要尽可能的大,所以svm模型建模可以分为两个子问题:
(1)分的对:怎么能让超平面将正负样本分的开;
(2)分的好:怎么能让距离超平面最近的点的距离尽可能的大。
对于第一个子问题:将样本分开,与感知机模型一样,我们也可以定义模型目标函数为:
$$ f(x)=sign(w^Tx+b) $$所以对每对样本$(x,y)$,只要满足$y\cdot (w^Tx+b)>0$,即表示模型将样本正确分开了
对于第二个子问题:怎么能让离超平面最近的点的距离尽可能的大,对于这个问题,又可以拆解为两个小问题:
(1)怎么度量距离? (2)距离超平面最近的点如何定义?
距离的度量很简单,可以使用高中时代就知道的点到面的距离公式:
$$
d=\frac{|w^Tx+b|}{||w||}
$$
距离超平面最近的点,我们可以强制定义它为满足$|w^Tx+b|=1$的点(注意,正负样本都要满足),为什么可以这样定义呢?我们可以反过来看,一个训练好的模型可以满足:(1)要使得正负样本距离超平面最近的点的距离都尽可能大,那么这个距离必然要相等,(2)参数$w,b$可以等比例的变化,而不会影响到模型自身,所以$|w^Tx+b|=1$自然也可以满足,所以这时最近的点的距离可以表示为:
$$ d^*=\frac{1}{||w||} $$同时第一个子问题的条件要调整为$y\cdot(w^Tx+b)\geq1$,而$\max d^*$可以等价的表示为$\min \frac{1}{2}w^Tw$,所以svm模型的求解可以表述为如下优化问题:
$$ \min_{w,b} \frac{1}{2}w^Tw \\ s.t.y_i(w^Tx_i+b)\geq 1,i=1,2,...,N $$二.原优化问题的对偶问题¶
对于上面优化问题的求解往往转化为对其对偶问题的求解,首先,构造其拉格朗日函数:
$$ L(w,b,\alpha)=\frac{1}{2}w^Tw+\sum_{i=1}^N \alpha_i(1-y_i(w^Tx_i+b)),\alpha=[\alpha_1,\alpha_2,...,\alpha_N] $$这时,原优化问题(设为$P$)就等价于:
$$ \min_{w,b}\max_{\alpha}L(w,b,\alpha)\\ s.t.\alpha_i\geq 0,i=1,2,...,N $$这里简单说明一下为什么等价,首先看里面$\max$那一层 $$\max_{\alpha}L(w,b,\alpha)\\ s.t.\alpha_i\geq 0,i=1,2,...,N$$
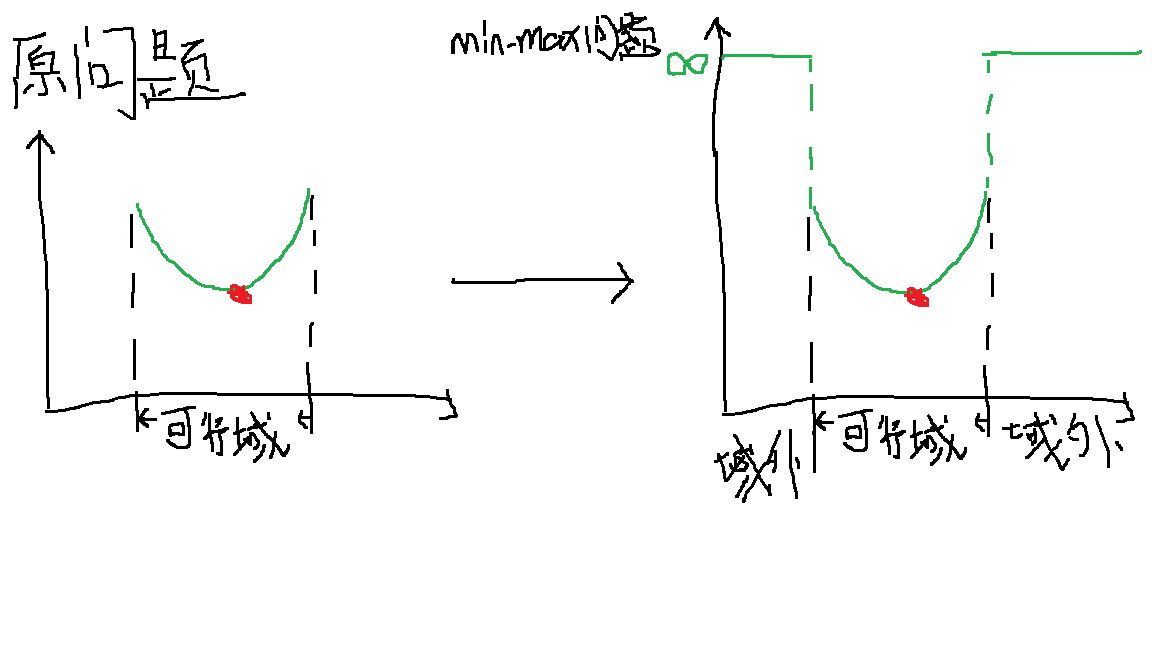
对每个样本都有约束条件$1-y_i(w^Tx_i+b)$,如果满足约束,即$\leq 0$,必有$\alpha_i(1-y_i(w^Tx_i+b))=0$,如果不满足,必有$\alpha_i(1-y_i(w^Tx_i+b))\rightarrow 正无穷$,所以,(1)如果所有样本均满足约束条件(即$w,b$在可行域内时),原问题与上面的$\min\max$问题等价,(2)如果有任意一个样本不满足约束,这时上面$\max$问题的函数取值为正无穷,外层再对其求$\min$会约束其只能在可行域内求最小值,所以两问题是等价的,简单手绘演示一下(两个问题的最优解都是红点标记):
假设对于问题$P$我们求得了最优解$w^*,b^*,\alpha^*$,则必有$L(w^*,b^*,\alpha^*)=L(w^*,b^*,0)$,所以有:
$$ \sum_{i=1}^N\alpha_i^*(1-y_i({w^*}^Tx_i+b^*))=0(条件1) $$而最优解自然也满足原始的约束条件,即:
$$ 1-y_i({w^*}^Tx_i+b)\leq0,i=1,2,...,N(条件2)\\ \alpha_i^*\geq0,i=1,2,...,N(条件3)\\ $$由条件1,2,3,我们可以得出更强地约束条件:
$$ \alpha_i^*(1-y_i({w^*}^Tx_i+b^*))=0,i=1,2,...,N(条件4) $$证明也很简单,由条件2,3可以知道,$\forall i,\alpha_i^*(1-y_i({w^*}^Tx_i+b^*))\leq0$都成立,要使条件1成立,则只能$\alpha_i^*(1-y_i({w^*}^Tx_i+b^*))=0,i=1,2,...,N$。
进一步的,可以推导出这样的关系:
$$ \forall \alpha_i^*>0\Rightarrow 1-y_i({w^*}^Tx_i+b^*)=0(关系1)\\ \forall 1-y_i({w^*}^Tx_i+b^*)<0\Rightarrow \alpha_i^*=0(关系2) $$所以条件4有个很形象的称呼:互补松弛条件,而对于满足关系1的样本,也有个称呼,叫支持向量
好的,我们继续看svm的对偶问题(设为$Q$)的定义:
$$
\max_{\alpha}\min_{w,b}L(w,b,\alpha)\\
s.t.\alpha_i\geq 0,i=1,2,...,N
$$
很幸运,svm的对偶问题$\max\min$与原问题$\min\max$等价(等价是指两个问题的最优值、最优解$w,b,\alpha$均相等,具体证明需要用到原问题为凸以及slater条件,可以参看《凸优化》),先看里层的$\min_{w,b} L(w,b,\alpha),$由于$L(w,b,\alpha)$是关于$w,b$的凸函数,所以对偶问题的最优解必然满足:$L(w,b,\alpha)$关于$w,b$的偏导为0,即:
$$ w=\sum_{i=1}^N\alpha_iy_ix_i(条件5)\\ 0=\sum_{i=1}^N\alpha_iy_i(条件6) $$消去$w,b$,可得对偶问题关于$\alpha$的表达式:
$$ \max_{\alpha} \sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j\\ s.t.\sum_{i=1}^N\alpha_iy_i=0,\\ \alpha_i\geq0,i=1,2,...,N $$显然,等价于如下优化问题(设为$Q^*$):
$$ \min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j-\sum_{i=1}^N\alpha_i\\ s.t.\sum_{i=1}^N\alpha_iy_i=0,\\ \alpha_i\geq0,i=1,2,...,N $$该问题是关于$\alpha$的凸二次规划(QP)问题,可以通过一些优化计算包(比如cvxopt)直接求解最优的$\alpha^*$,再由条件5,可知:
$$ w^*=\sum_{i=1}^N\alpha_i^*y_ix_i $$而关于$b^*$,我们可以巧妙求解:找一个样本点$(x_i,y_i)$,它满足对应的$\alpha_i^*>0$(即支持向量),利用关系1,可知$1-y_i({w^*}^Tx_i+b^*)=0$,所以:$b^*=y_i-{w^*}^Tx_i$
这里,条件2,3,4,5,6即是KKT条件,而且对于该优化问题,KKT条件还是最优解的充分条件(证明部分...可以参考《凸优化》),即满足KKT条件的解就是最优解。
三.SMO求解对偶问题最优解¶
关于对偶问题($Q^*$)可以使用软件包暴力求解,而且一定能得到最优解,但它的复杂度有点高:(1)变量数与样本数相同,每个变量$\alpha_i$对应样本$(x_i,y_i)$;(2)约束条件数也与样本数相同;而序列最小最优化化(sequential minimal optimization,SMO)算法是求解SVM对偶问题的一种启发式算法,它的思路是:每次只选择一个变量优化,而固定住其他变量,比如选择$\alpha_1$进行优化,而固定住$\alpha_i,i=2,3,...,N$,但由于我们的问题中有一个约束:$\sum_i^N\alpha_iy_i=0$,需要另外选择一个$\alpha_2$来配合$\alpha_1$做改变,当两者中任何一个变量确定后,另外一个也就随之确定了,比如确定$\alpha_2$后:
$$ \alpha_1=-y_i\sum_{i=2}^N\alpha_iy_i(关系3) $$选择两个变量后,如果优化?
我们在选择好两个变量后,如何进行优化呢?比如选择的$\alpha_1,\alpha_2$,由于剩余的$\alpha_3,\alpha_4,...,\alpha_N$都视作常量,在$Q^*$中可以忽略,重新整理一下此时的$Q^*$:
这里求解其实就很简单了,将关系3带入,消掉$\alpha_1$后可以发现,优化的目标函数其实是关于$\alpha_2$的二次函数(且开口朝上):
$$ \min_{\alpha_2}\frac{1}{2}(x_1-x_2)^T(x_1-x_2)\alpha_2^2+(-y_2\eta x_1^Tx_1+y_1\eta x_1^Tx_2+\frac{1}{2}y_2x_2^T\gamma-\frac{1}{2}y_2x_1^T\gamma-1+y_1y_2)\alpha_2\\ s.t.\alpha_2\geq0,y_1(\eta-\alpha_2y_2)\geq0 $$这里,$\eta=-\sum_{i=3}^N\alpha_iy_i,\gamma=\sum_{i=3}^N\alpha_iy_ix_i$
所以该问题无约束的最优解为:
$$ \alpha_2^{unc}=-\frac{-y_2\eta x_1^Tx_1+y_1\eta x_1^Tx_2+\frac{1}{2}y_2x_2^T\gamma-\frac{1}{2}y_2x_1^T\gamma-1+y_1y_2}{(x_1-x_2)^T(x_1-x_2)}(公式1) $$接下来,我们对上面的表达式做一些优化,大家注意每次迭代时,$\gamma,\eta$都有大量的重复计算(每次仅修改了$\alpha$的两个变量,剩余部分其实无需重复计算),而且对于$\alpha_1,\alpha_2$的更新也没有有效利用它上一阶段的取值(记作$\alpha_1^{old},\alpha_2^{old}$):
我们记:
$$
g(x)=\sum_{i=1}^N\alpha_iy_ix_i^Tx+b
$$
记:
$$
E_i=g(x_i)-y_i
$$
这里$g(x)$表示模型对$x$的预测值,$E_i$表示预测值与真实值之差,于是我们有:
另外:
$$ \eta=\alpha_1^{old}y_1+\alpha_2^{old}y_2 $$带入公式1,可得:
$$ \alpha_2^{unc}=\alpha_2^{old}+\frac{y_2(E_1^{old}-E_2^{old})}{\beta} $$这里$\beta=(x_1-x_2)^T(x_1-x_2)$,到这一步,可以发现计算量大大降低,因为$E_1^{old},E_2^{old}$可先缓存到内存中,但别忘了$\alpha_2$还有约束条件$\alpha_2\geq0,y_1(\eta-\alpha_2y_2)\geq0$,所以需要进一步对它的最优解分情况讨论:
当$y_1y_2=1$时, $$ \alpha_2^{new}=\left\{\begin{matrix} 0 & \alpha_2^{unc}<0\\ \alpha_2^{unc} & 0\leq\alpha_2^{unc}\leq \alpha_1^{old}+\alpha_2^{old}\\ \alpha_1^{old}+\alpha_2^{old} & \alpha_2^{unc}>\alpha_1^{old}+\alpha_2^{old} \end{matrix}\right. $$
当$y_1y_2=-1$时,
$$ \alpha_2^{new}=\left\{\begin{matrix} \alpha_2^{unc} & \alpha_2^{unc}\geq max\{0,\alpha_2^{old}-\alpha_1^{old}\}\\ max\{0,\alpha_2^{old}-\alpha_1^{old}\} & \alpha_2^{unc}< max\{0, \alpha_2^{old}-\alpha_1^{old}\} \end{matrix}\right. $$到这儿,我们可以发现,SMO算法可以极大的方便$Q^*$的求解,而且是以解析解方式,得到$\alpha_2^{new}$后,由于$\alpha_1^{new}y_1+\alpha_2^{new}y_2=\alpha_1^{old}y_1+\alpha_2^{old}y_2$,可得到$\alpha_1^{new}$的更新公式:
$$
\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new})
$$
最后,得到$w$的更新公式:
$$ w^{new}=w^{old}+(\alpha_1^{new}-\alpha_1^{old})y_1x_1+(\alpha_2^{new}-\alpha_2^{old})y_2x_2 $$对$b$和$E$的更新
而对于$b$的更新同样借助于$\alpha_1,\alpha_2$更新,在更新后,倾向于$\alpha_1^{new}>0,\alpha_2^{new}>0$,还记得前面的互补松弛条件吧(条件4),即对于$\alpha_i>0$的情况,必然要有$1-y_i(w^Tx_i+b)=0$成立,即$w^Tx_i+b=y_i$,所以对$(x_1,y_1),(x_2,y_2)$有如下关系:
$$ {w^{new}}^Tx_1+b=y_1(关系4)\\ {w^{new}}^Tx_2+b=y_2(关系5)\\ $$对关系4和关系5可以分别计算出$b_1^{new}=y_1-{w^{new}}^Tx_1,b_2^{new}=y_2-{w^{new}}^Tx_2$,对$b$的更新,可以取两者的均值:
$$ b^{new}=\frac{b_1^{new}+b_2^{new}}{2} $$接下来,对于$E_1,E_2$的更新就很自然了:
$$ E_1^{new}={w^{new}}^Tx_1+b^{new}-y_1\\ E_2^{new}={w^{new}}^Tx_2+b^{new}-y_2 $$那接下来还有一个问题,那就是$\alpha_1,\alpha_2$如何选择的问题
如何选择两个优化变量?
这可以启发式选择,分为两步:第一步是如何选择$\alpha_1$,第二步是在选定$\alpha_1$时,如何选择一个不错的$\alpha_2$:
$\alpha_1$的选择
选择$\alpha_1$同感知机模型类似,选择一个不满足KKT条件的点$(x_i,y_i)$,即不满足如下两种情况之一的点:
$$ \left\{\begin{matrix} \alpha_i=0\Leftrightarrow y_i(w^Tx_i+b)\geq1\\ \alpha_i>0\Leftrightarrow y_i(w^Tx_i+b)=1 \end{matrix}\right. $$$\alpha_2$的选择
对$\alpha_2$的选择倾向于选择使其变化尽可能大的点,由前面的更新公式可知是使$\mid E_1^{old}-E_2^{old}\mid$最大的点,所以选择的两个点$(x_1,y_1)$和$(x_2,y_2)$会更倾向于选择异类的点
四.代码实现¶
import numpy as np
import matplotlib.pyplot as plt
import copy
import random
import os
os.chdir('../')
from ml_models import utils
%matplotlib inline
#定义一个绘制决策边界以及支持向量的函数(并放到utils中)
def plot_decision_function(X, y, clf, support_vectors=None):
plot_step = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
np.arange(y_min, y_max, plot_step))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], alpha=0.8, c=y, edgecolor='k')
# 绘制支持向量
if support_vectors is not None:
plt.scatter(X[support_vectors, 0], X[support_vectors, 1], s=80, c='none', alpha=0.7, edgecolor='red')
"""
硬间隔支持向量机的smo实现,放到ml_models.svm模块
"""
class HardMarginSVM(object):
def __init__(self, epochs=100):
self.w = None
self.b = None
self.alpha = None
self.E = None
self.epochs = epochs
# 记录支持向量
self.support_vectors = None
def init_params(self, X, y):
"""
:param X: (n_samples,n_features)
:param y: (n_samples,) y_i\in\{0,1\}
:return:
"""
n_samples, n_features = X.shape
self.w = np.zeros(n_features)
self.b = .0
self.alpha = np.zeros(n_samples)
self.E = np.zeros(n_samples)
# 初始化E
for i in range(0, n_samples):
self.E[i] = np.dot(self.w, X[i, :]) + self.b - y[i]
def _select_j(self, best_i):
"""
选择j
:param best_i:
:return:
"""
valid_j_list = [i for i in range(0, len(self.alpha)) if self.alpha[i] > 0 and i != best_i]
best_j = -1
# 优先选择使得|E_i-E_j|最大的j
if len(valid_j_list) > 0:
max_e = 0
for j in valid_j_list:
current_e = np.abs(self.E[best_i] - self.E[j])
if current_e > max_e:
best_j = j
max_e = current_e
else:
# 随机选择
l = list(range(len(self.alpha)))
seq = l[: best_i] + l[best_i + 1:]
best_j = random.choice(seq)
return best_j
def _meet_kkt(self, w, b, x_i, y_i, alpha_i):
"""
判断是否满足KKT条件
:param w:
:param b:
:param x_i:
:param y_i:
:return:
"""
if alpha_i < 1e-7:
return y_i * (np.dot(w, x_i) + b) >= 1
else:
return abs(y_i * (np.dot(w, x_i) + b) - 1) < 1e-7
def fit(self, X, y2, show_train_process=False):
"""
:param X:
:param y2:
:param show_train_process: 显示训练过程
:return:
"""
y = copy.deepcopy(y2)
y[y == 0] = -1
# 初始化参数
self.init_params(X, y)
for _ in range(0, self.epochs):
if_all_match_kkt = True
for i in range(0, len(self.alpha)):
x_i = X[i, :]
y_i = y[i]
alpha_i_old = self.alpha[i]
E_i_old = self.E[i]
# 外层循环:选择违反KKT条件的点i
if not self._meet_kkt(self.w, self.b, x_i, y_i, alpha_i_old):
if_all_match_kkt = False
# 内层循环,选择使|Ei-Ej|最大的点j
best_j = self._select_j(i)
alpha_j_old = self.alpha[best_j]
x_j = X[best_j, :]
y_j = y[best_j]
E_j_old = self.E[best_j]
# 进行更新
# 1.首先获取无裁剪的最优alpha_2
eta = np.dot(x_i - x_j, x_i - x_j)
# 如果x_i和x_j很接近,则跳过
if eta < 1e-3:
continue
alpha_j_unc = alpha_j_old + y_j * (E_i_old - E_j_old) / eta
# 2.裁剪并得到new alpha_2
if y_i == y_j:
if alpha_j_unc < 0:
alpha_j_new = 0
elif 0 <= alpha_j_unc <= alpha_i_old + alpha_j_old:
alpha_j_new = alpha_j_unc
else:
alpha_j_new = alpha_i_old + alpha_j_old
else:
if alpha_j_unc < max(0, alpha_j_old - alpha_i_old):
alpha_j_new = max(0, alpha_j_old - alpha_i_old)
else:
alpha_j_new = alpha_j_unc
# 如果变化不够大则跳过
if np.abs(alpha_j_new - alpha_j_old) < 1e-5:
continue
# 3.得到alpha_1_new
alpha_i_new = alpha_i_old + y_i * y_j * (alpha_j_old - alpha_j_new)
# 4.更新w
self.w = self.w + (alpha_i_new - alpha_i_old) * y_i * x_i + (alpha_j_new - alpha_j_old) * y_j * x_j
# 5.更新alpha_1,alpha_2
self.alpha[i] = alpha_i_new
self.alpha[best_j] = alpha_j_new
# 6.更新b
b_i_new = y_i - np.dot(self.w, x_i)
b_j_new = y_j - np.dot(self.w, x_j)
if alpha_i_new > 0:
self.b = b_i_new
elif alpha_j_new > 0:
self.b = b_j_new
else:
self.b = (b_i_new + b_j_new) / 2.0
# 7.更新E
for k in range(0, len(self.E)):
self.E[k] = np.dot(self.w, X[k, :]) + self.b - y[k]
# 显示训练过程
if show_train_process is True:
utils.plot_decision_function(X, y2, self, [i, best_j])
utils.plt.pause(0.1)
utils.plt.clf()
# 如果所有的点都满足KKT条件,则中止
if if_all_match_kkt is True:
break
# 计算支持向量
self.support_vectors = np.where(self.alpha > 1e-3)[0]
# 利用所有的支持向量,更新b
self.b = np.mean([y[s] - np.dot(self.w, X[s, :]) for s in self.support_vectors.tolist()])
# 显示最终结果
if show_train_process is True:
utils.plot_decision_function(X, y2, self, self.support_vectors)
utils.plt.show()
def get_params(self):
"""
输出原始的系数
:return: w
"""
return self.w, self.b
def predict_proba(self, x):
"""
:param x:ndarray格式数据: m x n
:return: m x 1
"""
return utils.sigmoid(x.dot(self.w) + self.b)
def predict(self, x):
"""
:param x:ndarray格式数据: m x n
:return: m x 1
"""
proba = self.predict_proba(x)
return (proba >= 0.5).astype(int)
五.效果检验¶
from sklearn.datasets import make_classification
# 生成分类数据
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=2.0)
plt.scatter(data[:,0],data[:,1],c=target)
<matplotlib.collections.PathCollection at 0x19e700bb390>
#训练
svm = HardMarginSVM()
svm.fit(data, target)
plot_decision_function(data, target, svm, svm.support_vectors)
#可视化训练过程,建议在pycharm中运行,notebook会生成很多张图片
# svm = HardMarginSVM()
# svm.fit(data, target,show_train_process=True)
六.问题讨论¶