Principal Component Analysis (PCA)¶
Na aprendizagem de máquina não supervisionada temos algoritmos que trabalham com dados que não possuem classificações prévias para treinamento. Assim, o desafio se torna mais subjetivo que na abordagem supervisionada, pois não existe um objetivo claro para ser classificado ou previsto. Por isso, a aprendizagem não supervisionada é muitas vezes usada como parte de uma análise exploratória dos dados.
Um das formas mais comum de exploração dos dados é através da sua visualização num espaço N-dimensional, no qual cada dimensão representa uma característica. Ou seja, para dados com duas características usamos um plano e para dados com três características um espaço tridimensional, mas a partir de quatro características temos um problema, pois só conseguimos ver até a terceira dimensão.
Para conseguir visualizar dados com muitas dimensões, podemos usar a Principal Component Analysis (PCA). Ela é uma técnica que encontra uma representação em menos dimensões para um conjunto de dados, com a preocupação em manter ao máximo a relação entre os dados originais.
A ideia principal da PCA é que num conjunto de dados representado por N dimensões, nem todas elas são interessantes. Em outras palavras, nem todas as características dos exemplos servem para diferenciá-los.
Por exemplo, usando um conjunto de dados de pessoas com o objetivo de tentar entender as relações entre quem paga ou não paga um empréstimo, provavelmente os dados sobre a altura das pessoas não ajudam a diferenciar bons pagadores de maus pagadores. Além disso, num conjunto de dados, existem características que importam mais que outras, ainda nesse exemplo, o salário pode influenciar mais que a idade.
Assim, a PCA procura novas dimensões nos dados que sirvam para diferenciar os dados da melhor forma possível.
Dados¶
Para explicar o algoritmo, inicialmente vamos trabalhar com exemplos que possuem apenas 2 características. Isso vai facilitar a visualização dos dados e o entendimento do processo. Nesse caso usaremos a PCA para reduzir a dimensão do conjunto de dados de duas dimensões para uma dimensão.
Abaixo temos os pontos que trabalharemos nesse exemplo.
from bokeh.io import show, output_notebook
from bokeh.plotting import figure
output_notebook()
x = [2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]
y = [2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9]
p = figure(plot_width=350, plot_height=350, x_range=(0, 4), y_range=(0, 4))
p.circle(x, y, radius=0.04)
show(p, notebook_handle=True)
Pré-processamento¶
No pré-processamento vamos subtrair, em cada um dos exemplos dos dados, a média de cada dimensão. Para isso, calculamos a média na dimensão x, que chamaremos de $\overline{x}$ e a média na dimensão y denotada por $\overline{y}$. Em seguida, para cada um dos exemplos atribuiremos a coordenada $x$ o valor $x-\overline{x}$ e para a coordenada $y$ o valor $y-\overline{y}$.
import numpy as np
x_mean = np.mean(x)
y_mean = np.mean(y)
x = [i - x_mean for i in x]
y = [i - y_mean for i in y]
Após esse procedimento, os dados passarão a ter média zero, fazendo com que eles fiquem centralizados em relação à origem. No gráfico abaixo temos os pontos centralizados.
p = figure(plot_width=350, plot_height=350)
p.circle(x, y, radius=0.035)
show(p, notebook_handle=True)
<Bokeh Notebook handle for In[3]>
Encontrando as novas dimensões¶
Uma dimensão ou componente principal pode ser representado por uma reta, plano ou hiperplano no espaço. O gráfico a seguir exibe uma reta que representa o primeiro componente principal encontrado ao executarmos a PCA usando os dados apresentados anteriormente.
p = figure(plot_width=350, plot_height=350)
p.circle(x, y, radius=0.035)
p.line([-0.6778734*2 , -0.6778734*-2], [-0.73517866*2 , -0.73517866*-2], line_width=2, color="black")
show(p, notebook_handle=True)
<Bokeh Notebook handle for In[4]>
Para representar os pontos que estão no espaço bidimensional numa única dimensão, basta projetá-los no componente principal. A figura abaixo mostra as projeções dos pontos na reta (esquerda) e os pontos representados em apenas uma dimensão (direita).
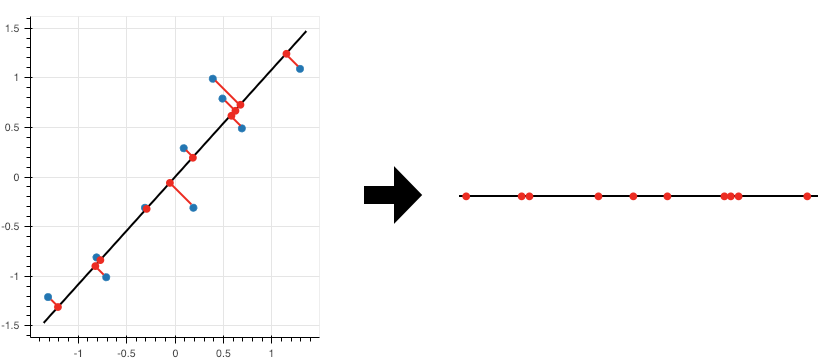
A reta que representa o componente principal segue a direção na qual os dados mais variam. Com isso, se projetarmos os pontos do espaço bidimensional nela, então a variância dos pontos na reta é a maior possível. Também podemos entender a reta encontrada como a reta que minimiza a soma do quadrado das distâncias perpendiculares dos pontos até a reta.
Matriz de covariância¶
Para encontrar os componentes principais, o primeiro passo é calcular a matriz de covariância. Mas para isso, primeiro precisamos entender o que é a covariância, que é definida como a medida do grau de variação conjunta de duas variáveis.
Dadas duas variáveis X e Y, a covariância é positiva quando elas tendem a variar no mesmo sentido, isto é, os maiores valores de X estão associados aos maiores valores de Y, assim como os menores valores de X estão associados aos menores valores de Y. No caso contrário, no qual os menores valores de X estão associados aos maiores valores de Y e os maiores valores de X estão associados aos menores valores de Y, a covariância tem valor negativo.
A fórmula para calcular a covariância com os dados centralizados é:
$$cov(X, Y) = \frac{1}{n-1} \sum_{i}^{n}X_iY_i$$Onde $X_i$ é o valor da variável X do i-ésimo exemplo e $Y_i$ é o valor da variável Y do i-ésimo exemplo.
A função abaixo calcula a covariância de duas variáveis. Os valores das variáveis são passados como listas, o parâmetro x recebe os valores da primeira variável e o parâmetro y da segunda variável.
def covariance(x, y):
result = 0
for i in range(len(x)):
result += x[i]*y[i]
return result/(len(x)-1)
Passando os dados do exemplo para função temos:
covariance(x, y)
0.6154444444444445
Para um dataset com duas características, nós podemos apenas calcular a covariância entre elas. Entretanto, para dados com mais características, que são representados por mais dimensões, temos mais possibilidades. Por exemplo, com três dimensões (X, Y e Z), é possível calcular $cov(X, Y)$, $cov(X, Z)$ e $cov(Y,Z)$.
Com isso, a matriz de covariância é utilizada para sumarizar todas as covariâncias calculadas para qualquer número de dimensões. A matriz de covariância tem N linhas e N colunas, sendo N o número de dimensões. Dessa forma, para três dimensões, a matriz tem tamanho 3x3 e seus elementos são:
$$ C = \begin{bmatrix} cov(x,x) & cov(x,y) & cov(x,z) \\ cov(y,x) & cov(y,y) & cov(y,z) \\ cov(z,x) & cov(z,y) & cov(z,z) \end{bmatrix} $$Note que ao longo da diagonal principal, tem-se a covariância de uma dimensão em relação a ela mesma. Esse valor é chamado de variância. Além disso, é importante ressaltar que $cov(x,y) = cov(y,x)$ para qualquer x e y, assim a matriz é simétrica em relação à diagonal principal.
A função a seguir calcula a matriz de covariância para N dimensões que são passadas em uma lista como parâmetro.
def covariance_matrix(dimensions):
covariance_matrix = []
for i in range(len(dimensions)):
covariance_matrix.append([])
for j in range(len(dimensions)):
covariance_matrix[-1].append(covariance(dimensions[i], dimensions[j]))
return covariance_matrix
covariance_matrix([x, y])
[[0.6165555555555556, 0.6154444444444445], [0.6154444444444445, 0.7165555555555555]]
Outra forma de calcular a matriz de covariância é utilizando a função cov() do numpy:
np.cov(x, y)
array([[0.61655556, 0.61544444],
[0.61544444, 0.71655556]])
Autovalores e Autovetores¶
O próximo passo para encontrar os componentes principais é calcular os autovalores e autovetores da matriz de covariância. Os autovetores encontrados são os vetores utilizados para projetar os dados maximizando a variância. Anteriormente usamos uma reta para representar uma dimensão, mas lembre-se que podemos definir uma reta a partir de um vetor. Já os autovalores trazem o valor da variância dos dados projetados no autovetor correspondente.
Podemos calcular os autovalores e autovetores através da função eig() do numpy:
from numpy.linalg import eig
eigenvalues, eigenvectors = eig(np.cov(x, y))
print(eigenvalues)
print(eigenvectors)
[0.0490834 1.28402771] [[-0.73517866 -0.6778734 ] [ 0.6778734 -0.73517866]]
Nesse caso, os autovetores são dados pelas colunas da matriz eigenvectors, assim para acessar os autovetores vamos usar:
print(f"Autovetor 0: {eigenvectors[:,0]}")
print(f"Autovetor 1: {eigenvectors[:,1]}")
Autovetor 0: [-0.73517866 0.6778734 ] Autovetor 1: [-0.6778734 -0.73517866]
Para os autovalores, o primeiro elemento é o autovalor associado ao primeiro autovetor, o segundo elemento ao segundo autovetor e assim sucessivamente.
print(f"Autovalor 0: {eigenvalues[0]}")
print(f"Autovalor 1: {eigenvalues[1]}")
Autovalor 0: 0.04908339893832736 Autovalor 1: 1.2840277121727839
Escolhendo os componentes principais¶
Seguindo o exemplo, vamos escolher um autovetor para reduzir o dataset de duas dimensões para uma dimensão. Para isso, vamos escolher o autovetor com o maior autovalor, ou seja, o autovetor [-0.6778734 -0.73517866].
principal_component = eigenvectors[:,1]
Colocando o vetor no gráfico a partir da origem e com tamanho 1, temos:
from bokeh.models import Arrow, NormalHead
vector_size = 1
pcx = principal_component[0]
pcy = principal_component[1]
p = figure(plot_width=350, plot_height=350)
p.circle(x, y, radius=0.035)
p.add_layout(Arrow(end=NormalHead(fill_color="black", size=15),
x_start=0, y_start=0,
x_end=pcx*vector_size, y_end=pcy*vector_size,
line_width=2))
show(p, notebook_handle=True)
<Bokeh Notebook handle for In[13]>
O vetor do gráfico acima tem tamanho 1, mas se expandirmos ele nas suas duas direções, encontraremos a mesma reta que minimiza as distâncias quadráticas perpendiculares. O gráfico a seguir mostra a reta em vermelho.
p = figure(plot_width=350, plot_height=350)
p.circle(x, y, radius=0.035)
p.add_layout(Arrow(end=NormalHead(fill_color="black", size=15),
x_start=0, y_start=0,
x_end=pcx*vector_size, y_end=pcy*vector_size,
line_width=2))
p.line([pcx*2 , pcx*-2], [pcy*2 , pcy*-2], line_width=2, color="red")
show(p, notebook_handle=True)
<Bokeh Notebook handle for In[14]>
Projetando os valores¶
Para projetar um ponto no componente principal calculamos o produto escalar entre o vetor que representa um ponto e o vetor que representa o componente principal. Dessa forma, o ponto (0.69, 0.49) tem o seguinte valor na nova dimensão:
np.dot([0.69, 0.49], principal_component)
-0.8279701862010879
Fazendo para todos os pontos do exemplo, temos:
points = np.stack([x,y], axis=1) # criando uma matriz na qual cada linha é um ponto do exemplo
oned_points = []
for point in points:
oned_points.append(np.dot(point, principal_component))
p = figure(plot_width=350, plot_height=250)
p.circle(oned_points, 0, radius=0.035)
show(p, notebook_handle=True)
<Bokeh Notebook handle for In[17]>
Como esperado, os pontos estão todos representados em uma única dimensão. Notem que as distâncias entre os pontos continuam parecidas com as distâncias entre eles no gráfico de duas dimensões.
Dados com 3 dimensões ou mais¶
O PCA é especialmente importante na visualização de dados com 3 ou mais dimensões. No exemplo anterior, usamos um dataset com dados bidimensionais e, usando o PCA, representamos eles em uma dimensão. A seguir todo o algoritmo vai ser executado para o conhecido dataset de flores íris. Esse dataset contém dados sobre 150 flores, cada uma delas representada por quatro características.
from sklearn import datasets
dataset = datasets.load_iris()
iris_data = dataset.data
iris_data.shape
(150, 4)
Com 4 dimensões, não é possível visualizar o dataset. Assim, vamos executar o PCA para representar os dados utilizando menos dimensões.
O primeiro passo é o pré-processamento para centralizar os dados.
means = iris_data.mean(axis=1, keepdims=True) # calculando a média de cada uma das flores
iris_data = iris_data - means
iris_data.shape
(150, 4)
Em seguida, calculamos a matriz de covariância.
cov_matrix = np.cov(iris_data, rowvar=False)
cov_matrix
array([[ 0.07877002, 0.03580045, -0.06437248, -0.05019799],
[ 0.03580045, 0.94506532, -0.97777517, -0.0030906 ],
[-0.06437248, -0.97777517, 1.04399329, -0.00184564],
[-0.05019799, -0.0030906 , -0.00184564, 0.05513423]])
Com a matriz em mãos, podemos calcular os autovalores e autovetores.
eigenvalues, eigenvectors = eig(cov_matrix)
print(eigenvalues)
print(eigenvectors)
[ 1.97623957e+00 1.18269289e-01 -2.87303072e-16 2.84540080e-02] [[ 0.03760102 0.78022871 0.5 0.3739376 ] [ 0.68827047 -0.10694172 0.5 -0.5146331 ] [-0.72447773 -0.05992256 0.5 -0.47068174] [-0.00139375 -0.61336443 0.5 0.61137725]]
Analisando os autovalores, pode-se perceber que o primeiro possui o maior valor, então, se quisermos representar os dados das flores íris usando uma dimensão, projetaremos eles no primeiro autovetor. Entretanto, nesse exemplo, podemos usar mais dimensões para representar os pontos em duas ou três dimensões.
Para reduzir para duas dimensões, escolheremos os dois maiores autovalores e os seus autovetores correspondentes. Observando os valores calculados, tem-se que os dois maiores autovalores são os dois primeiros. Com isso, vamos projetar os dados num plano representado pelos dois primeiros autovetores, assim exibindo os dados num espaço bidimensional.
Para projetar um ponto no espaço bidimensional multiplicamos o vetor do ponto pela matriz contendo os dois primeiros autovetores.
first_iris = iris_data[0]
print(first_iris)
np.matmul([eigenvectors[0], eigenvectors[1]], first_iris)
[ 2.55 0.95 -1.15 -2.35]
array([-0.6166535 , 2.28788285])
Fazendo o cálculo para todos os pontos:
twod_x = []
twod_y = []
for point in iris_data:
new_point = np.matmul([eigenvectors[0], eigenvectors[1]], point)
twod_x.append(new_point[0])
twod_y.append(new_point[1])
O dataset além de trazer as características das flores, também tem a classificação de cada uma. São três tipos diferentes e no gráfico abaixo cada tipo tem uma cor específica.
Usando o resultado do PCA, veja os pontos representados em duas dimensões:
colors = ["red", "blue", "green"]
p = figure(plot_width=350, plot_height=350)
p.circle(twod_x, twod_y, radius=0.010, color=[colors[x] for x in dataset.target])
show(p, notebook_handle=True)
<Bokeh Notebook handle for In[24]>
Para finalizar, vamos representar os dados em 3 dimensões. Para isso, multiplicamos cada ponto pelos autovetores com os três maiores autovalores.
threed_x = []
threed_y = []
threed_z = []
for point in iris_data:
new_point = np.matmul([eigenvectors[0], eigenvectors[1], eigenvectors[3]], point)
threed_x.append(new_point[0])
threed_y.append(new_point[1])
threed_z.append(new_point[2])
Os pontos em 3 dimensões podem ser vistos no gráfico abaixo:
import plotly
import plotly.graph_objs as go
plotly.offline.init_notebook_mode()
plot = go.Scatter3d(x=threed_x, y=threed_y, z=threed_z, mode='markers',
marker=dict(size=5, color=[colors[x] for x in dataset.target]))
layout = go.Layout(width=800, height=400, margin=go.layout.Margin(l=10, r=10, b=10, t=10, pad=10))
data = [plot]
plotly.offline.iplot({'data': data, 'layout': layout})