Representation¶
- Activity of neurons change over time

- This probably means something
- Sometimes it's pretty clear what it means
Some sort of mapping between activity and some value
- my location
- head tilt
- image
- remembered location
Let's call this "representation"
- And let's assume this is true for every neuron in the brain
- There's always some value that its activity relates to
Representation formalism¶
- value being represented: $x$
- neural activity: $a$
Encoding and decoding¶
- Lossless code:
- encoding: $a = f(x)$
- decodng: $x = f^{-1}(a)$
- Lossy code:
- encoding: $a= f(x)$
- decoding: $\hat{x} = g(a) \approx x$
Distributed representation¶
- not just one neuron per $x$ value
- many different $a$ values for a single $x$
- encoding: $a_i = f_i(x)$
- decoding: $\hat{x} = g(a_0, a_1, a_2, a_3, ...)$
Example: binary representation¶
$$ a_i = \begin{cases} 1 &\mbox{if } x \mod {2^{i+1}} \ge 2^{i} \\ 0 &\mbox{otherwise} \end{cases} $$$$ \hat{x} = a_0*1 + a_1*2+ a_2*4 + a_3*8 $$$x = 13$
$a_0 = 1$
$a_1 = 0$
$a_2 = 1$
$a_3 = 1$
$\hat{x} = 1*1+0*2+1*4+1*8 = 13$
Linear decoding¶
Special case
write decoder as $\hat{x} = \sum_i(a_i d_i)$
linear decoding is nice and simple
- works fine with non-linear encoding (!)
We'll use linear decoding, but what about the encoding?
Neuron encoding¶
$a_i = f_i(x)$
- What do we know about neurons?

Firing rate goes up as total input current goes up
- $a_i = G_i(J)$
What is $G_i$?
- depends on how detailed a neuron model we want.
# Rectified linear neuron
import numpy
def rectified_linear(J, gain=100):
return numpy.maximum(J*gain,0)
J = numpy.linspace(-1,1,100)
import pylab
pylab.plot(J, rectified_linear(J))
pylab.xlabel('J (current)')
pylab.ylabel('$a$ (Hz)')
pylab.show()
Leaky integrate-and-fire neuron¶
$ a = {1 \over {\tau_{ref}-\tau_{RC}ln(1-{1 \over J})}}$
# Leaky integrate and fire
import numpy
import syde556
J = numpy.linspace(-1,10,100)
import pylab
pylab.plot(J, syde556.lif(J, tau_ref=0.002, tau_rc=0.02))
pylab.xlabel('J (current)')
pylab.ylabel('$a$ (Hz)')
pylab.show()
These are called "tuning curves"
Neurons seem to be sensitive to particular values of $x$
What's the mapping between $x$ and $J$?
- Sometimes it's nice and simple:

- But not often:


- Is there a general form?
Neural encoding¶
- We think there is
- Something generic and simple
- that covers all the above cases (and more)
- Let's start with the simplest

Note that they're graphing $a$, not $J$
- $a$ is much easier to measure
$x$ is the volume of the sound in this case
Any ideas?
import numpy
import syde556
x = numpy.linspace(-100,0,100)
import pylab
pylab.plot(x, syde556.lif(x*1+50))
pylab.plot(x, syde556.lif(x*0.1+10))
pylab.plot(x, syde556.lif(x*0.05+5))
pylab.plot(x, syde556.lif(x*0.1+4))
pylab.xlabel('x')
pylab.ylabel('a')
pylab.show()
$ J = \alpha x + J^{bias} $
- but what about type (c) in this graph?

- easy enough:
$ J = - \alpha x + J^{bias} $
- but what about type(b)? Or these ones?

- There's usually some $x$ which gives a maximum firing rate
- and thus a maximum $J$
- firing rate (and $J$) decrease as you get farther from the preferred $x$ value
- So something like $J = \alpha [sim(x, x_{pref})] + J^{bias}$
- What sort of similarity measure?
- Let's think about $x$ for a moment
- $x$ can be anything... scalar, vector, etc.
- does thinking of it as a vector help?
The Encoding Equation¶
- Here is the general form we use for everything
- $J = \alpha x \cdot e + J^{bias} $
- $\alpha$ is a gain term (constrained to always be positive)
- $J^{bias}$ is a constant bias term
- $e$ is the encoder, or the preferred direction vector
- To simplify life, we always assume $e$ is of unit length
- otherwise we could combine $\alpha$ and $e$
- In the 1D case, $e$ is either +1 or -1
- In higher dimensions, what happens?
import numpy
e = numpy.array([1.0, 1.0])
e = e/numpy.linalg.norm(e)
a = numpy.linspace(-1,1,50)
b = numpy.linspace(-1,1,50)
X,Y = meshgrid(a, b)
import pylab
from mpl_toolkits.mplot3d.axes3d import Axes3D
fig = pylab.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
p = ax.plot_surface(X, Y, syde556.lif((X*e[0]+Y*e[1])+1.5), linewidth=0, cstride=1, rstride=1, cmap=pylab.cm.jet)
- But that's not how people normally plot it
- It might not make sense to sample every possible x
- Instead they might do some subset
- For example, what if we just plot the points around the unit circle?
theta, x = syde556.sample_around_unit_circle(100)
e = numpy.array([1.0, 0.0])
alpha = 1
bias = 1.5
J = alpha*numpy.dot(x.T, e)+bias
pylab.plot(theta, syde556.lif(J))
pylab.xlabel('angle')
pylab.ylabel('firing rate')
pylab.xlim(-numpy.pi, numpy.pi)
pylab.show()
- that starts looking a lot more like the real data
Notation¶
encoding
- $a_i = G(\alpha_i x \cdot e_i + J^{bias}_i)$
decoding
- $\hat{x} = \sum_i (a_i d_i)$
The textbook uses $\phi$ for $d$ and $\tilde \phi$ for $e$
- I find this very confusing
- We're switching to $d$ (for decoder) and $e$ (for encoder)
Decoder¶
But where do we get $d_i$ from?
- $\hat{x}=\sum(a_i d_i)$
Find the optimal $d_i$
- How?
- Math
Solving for $d$¶
- Minimize the average error over all $x$
$ E = {\int_{-1}^1 (x-\hat{x})^2 dx } \over {2}$
- Substitute for $\hat{x}$
$ E = {1 \over 2} \int_{-1}^1 (x-\sum_i(a_i d_i))^2 dx $
- Take the derivative with respect to $d_i$
$ {{\partial E} \over {\partial d_i}} = {1 \over 2} \int_{-1}^1 2 [x-\sum_j(a_j d_j)](-a_i) dx $
$ {{\partial E} \over {\partial d_i}} = - \int_{-1}^1 a_i x dx + \int_{-1}^1 \sum_j(a_j d_j a_i) dx $
- At the minimum, $ {{\partial E} \over {\partial d_i}} = 0$
$ \int_{-1}^1 a_i x dx = \int_{-1}^1 \sum_j(a_j d_j a_i) dx $
$ \int_{-1}^1 a_i x dx = \sum_j (\int_{-1}^1 a_i a_j dx)d_j $
- That's a system of $N$ equations and $N$ unknowns
- In fact, we can rewrite this in matrix form
$ \Upsilon = \Gamma d $
where
$ \Upsilon_i = {1 \over 2} \int_{-1}^1 a_i x dx$
$ \Gamma_{ij} = {1 \over 2} \int_{-1}^1 a_i a_j dx $
- Do we have to do the integral over all $x$?
- Approximate the integral by sampling over $x$
- $S$ is the number of $x$ values to use ($S$ for samples)
$ \sum_x a_i x / S = \sum_j (\sum_x a_i a_j /S )d_j $
$ \Upsilon = \Gamma d $
where
$ \Upsilon_i = \sum_x a_i x / S$
$ \Gamma_{ij} = \sum_x a_i a_j / S $
- Notice that if $A$ is the matrix of activities (the firing rate for each neuron for each $x$ value), then $\Gamma=A^T A / S$ and $\Upsilon=A^T x / S$
So given
$ \Upsilon = \Gamma d $
then
$ d = \Gamma^{-1} \Upsilon $
or, equivalently
$ d_i = \sum_j \Gamma^{-1}_{ij} \Upsilon_j $
import numpy
import syde556
N = 30
x = numpy.linspace(-1, 1, 100)
encoders = numpy.random.choice([-1, 1], N)
alpha = numpy.random.uniform(0.5,2, N)
bias = numpy.random.uniform(-2, 2, N)
A = syde556.activity(x, encoders, alpha, bias)
d = syde556.decoders(A, x)
xhat = numpy.dot(A, d)
figure()
plot(x, A)
xlabel('x')
ylabel('firing rate (Hz)')
figure()
plot(x, x)
plot(x, xhat)
xlabel('$x$')
ylabel('$\hat{x}$')
ylim(-1, 1)
xlim(-1, 1)
figure()
plot(x, xhat-x)
xlabel('$x$')
ylabel('$\hat{x}-x$')
xlim(-1, 1)
show()
print 'RMSE', np.sqrt(np.average((x-xhat)**2))
RMSE 0.0102481110469
- What happens to the error with more neurons?
Noise¶
- Neurons aren't perfect
- axonal jitter
- neurotransmitter vesicle release failure (~80%)
- amount of neurotransmitter per vesicle
- thermal noise
- ion channel noise (# of channels open and closed)
- network effects
- more information: http://icwww.epfl.ch/~gerstner/SPNM/node33.html
- How do we include this noise as well?
- make the model more complicated
- simple approach: add gaussian random noise to $a_i$
- set noise standard deviation $\sigma$ to 20% of maximum firing rate
- each $a_i$ value for each $x$ value gets a different noise value added to it
- What effect does this have on decoding?
import numpy
import syde556
N = 30
x = numpy.linspace(-1, 1, 100)
encoders = numpy.random.choice([-1, 1], N)
alpha = numpy.random.uniform(0.5,2, N)
bias = numpy.random.uniform(-2, 2, N)
A = syde556.activity(x, encoders, alpha, bias)
A_noisy = syde556.add_noise(A, 0.2)
d = syde556.decoders(A, x)
xhat = numpy.dot(A_noisy, d)
figure()
plot(x, A_noisy)
xlabel('x')
ylabel('firing rate (Hz)')
figure()
plot(x, x)
plot(x, xhat)
ylim(-2, 2)
xlim(-1, 1)
show()
print 'RMSE', np.sqrt(np.average((x-xhat)**2))
RMSE 1.02002633442
- what if we just increase the number of neurons? Will that help?
Taking noise into account¶
include noise while solving for decoders
- introduce noise term $\eta$
$ \hat{x} = \sum_i(a_i+\eta)d_i $
$ E = {1 \over 2} \int_{-1}^1 [x-\hat{x}]^2 dx $
$ E = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i+\eta)d_i]^2 dx $
$ E = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i d_i) - \sum(\eta d_i)]^2 dx $
- assume noise is gaussian, independent, mean zero, and has the same variance for each neuron
- $\eta = N(0, \sigma)$
- so all the noise cross-terms disappear
$ E = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i d_i)]^2 dx + \sum_{i,j}(d_i d_j \eta_i \eta_j) $
$ E = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i d_i)]^2 dx + \sum_{i}(d_i d_i \eta_i \eta_i) $
- and since the average of $\eta_i \eta_i$ noise is its variance $\sigma^2$, we get
$ E = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i d_i)]^2 dx + \sigma^2 \sum_i d_i^2 $
- The practical result is that, when computing the decoder, we get
$ \Gamma_{ij} = \sum_x a_i a_j / S + \sigma^2 \delta_{ij}$
where $\delta_{ij}$ is the Kronecker delta: http://en.wikipedia.org/wiki/Kronecker_delta
to simplfy computing this using matrices, this can be written as $\Gamma=A^T A /S + \sigma^2 I$
import numpy
import syde556
N = 300
x = numpy.linspace(-1, 1, 100)
encoders = numpy.random.choice([-1, 1], N)
alpha = numpy.random.uniform(0.5,2, N)
bias = numpy.random.uniform(-2, 2, N)
A = syde556.activity(x, encoders, alpha, bias)
d = syde556.decoders(A, x, noise=0.2, dx=2.0/len(x))
A_noisy = syde556.add_noise(A, 0.2)
xhat = numpy.dot(A_noisy, d)
figure()
plot(x, A_noisy)
xlabel('x')
ylabel('firing rate (Hz)')
figure()
plot(x, x)
plot(x, xhat)
ylim(-2, 2)
xlim(-1, 1)
show()
print 'RMSE', np.sqrt(np.average((x-xhat)**2))
RMSE 0.0555618233321
Number of neurons¶
- What happens to the error with more neurons?
- Note that the error has two parts:
$ E = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i d_i)]^2 dx + \sigma^2 \sum_i d_i^2 $
- Error due to static distortion (i.e. the error introduced by the decoders themselves)
- This is present regardless of noise
$ E_{distortion} = {1 \over 2} \int_{-1}^1 [x-\sum_i(a_i d_i)]^2 dx $
- Error due to noise
$ E_{noise} = \sigma^2 \sum_i d_i^2 $
- What do these look like as number of neurons $N$ increases?
import numpy
import syde556
noise = 0.2
x = numpy.linspace(-1, 1, 100)
dx = 2.0/100
Ns = numpy.array([8, 16, 32, 64, 128, 256, 512])
E_distortion = []
E_noise = []
for N in Ns:
encoders = numpy.random.choice([-1, 1], N)
intercepts = numpy.random.uniform(-0.9, 0.9, N)
max_rates = numpy.random.uniform(100, 200, N)
alpha, bias = syde556.find_alpha_and_bias(intercepts, max_rates)
A = syde556.activity(x, encoders, alpha, bias)
d = syde556.decoders(A, x, noise=noise, dx=dx)
A_noisy = syde556.add_noise(A, noise)
xhat = numpy.dot(A, d)
xhat_noisy = numpy.dot(A_noisy, d)
E_d = syde556.compute_error_distortion(x, xhat)
E_n = syde556.compute_error_noise(noise*np.max(A), d)
E_distortion.append(E_d)
E_noise.append(E_n)
figure()
loglog(Ns, E_distortion, label='$E_{dist}$')
loglog(Ns, 1.0/Ns, label='$1/N$')
loglog(Ns, 0.1/(Ns**2), label='$0.1/N^2$')
xlabel('N')
ylabel('E distortion')
legend(loc='best')
figure()
loglog(Ns, E_noise, label='$E_{noise}$')
loglog(Ns, 0.2/(Ns), label='$0.2/N$')
xlabel('N')
ylabel('E noise')
legend(loc='best')
show()
- Distortion error is proportional to $1/N^2$
- Noise error is proportional to $1/N$
- Remember this error $E$ is defined as
$ E = {1 \over 2} \int_{-1}^1 (x-\hat{x})^2 dx $
So that's actually a squared error term
Also, as number of neurons is greater than 100 or so, the error is dominated by the noise term ($1/N$).
Examples¶
- Methodology for building models with the Neural Engineering Framework
- System Description: Describe the system of interest in terms of the basic principles
- Design Specification: Add in neurobiological details that act as constraints (firing rates, tuning curves, noise levels, neuron models, etc.)
- Implement the model
Example 1: Horizontal Eye Control¶
From http://www.nature.com/nrn/journal/v3/n12/full/nrn986.html

There are also neurons whose response goes the other way. These neurons are directly connected to the muscle controlling the horizontal direction of the eye, and that's the only thing that muscle does, so we're pretty sure this is what's being repreesnted.
System Description
- We've only done the first NEF principle, so that's all we'll worry about
- What is being represented?
- $x$ is the horizontal position
Design Specification
- range of values for $x$: -60 degrees to +60 degrees
- tuning curves: extremely linear (high $\tau_{RC}$)
- some have $e=1$, some have $e=-1$
- these are often called "on" and "off" neurons, respectively
- firing rates of up to 300Hz
- normal levels of noise: $\sigma$ is 20% of maximum firing rate
- the book goes a bit higher, with $\sigma^2=0.1$, meaning that $\sigma = \sqrt{0.1} \approx 0.32$ times the maximum firing rate
Implementation
- tuning curves
import numpy
import syde556
N = 40
tau_rc = 0.2
x = numpy.linspace(-1, 1, 100)
encoders = numpy.random.choice([1, -1], N)
intercepts = numpy.random.uniform(-0.9, 0.9, N)
max_rates = numpy.random.uniform(250, 300, N)
alpha, bias = syde556.find_alpha_and_bias(intercepts, max_rates, tau_rc=tau_rc)
A = syde556.activity(x, encoders, alpha, bias, tau_rc=tau_rc)
figure()
plot(x, A)
xlabel('x')
ylabel('firing rate (Hz)')
show()
- How good is the representation?
noise = 0.2
dx = 2.0/100
d = syde556.decoders(A, x, noise=noise, dx=dx)
A_noisy = syde556.add_noise(A, noise)
xhat = numpy.dot(A_noisy, d)
print 'RMSE with %d neurons is %g'%(N, np.sqrt(np.average((x-xhat)**2)))
figure()
plot(x, x)
plot(x, xhat)
ylim(-1, 1)
xlim(-1, 1)
xlabel('$x$')
ylabel('$\hat{x}$')
show()
RMSE with 40 neurons is 0.0778816
- Possible questions
- How many neurons do we need for a particular level of accuracy?
- What happens with different firing rates?
- What happens with different distributions of x-intercepts?
Example 2: Arm Movements¶



System Description
- What is being represented?
- $x$ is the hand position
- Note that this is different from what Georgopoulos talks about in this initial paper
- Initial paper only looks at those 8 positions, so it only talks about direction of movement (angle but not magnitude)
- More recent work in the same area shows the cells do respond to both (Fu et al, 1993; Messier and Kalaska, 2000)
Design Specification
- range of values for $x$: Anywhere within a unit circle (or perhaps some other radius)
- encoders: randomly distributed around the unit circle
- firing rates of up to 60Hz
- normal levels of noise: $\sigma$ is 20% of maximum firing rate
- the book goes a bit higher, with $\sigma^2=0.1$, meaning that $\sigma = \sqrt{0.1} \approx 0.32$ times the maximum
Implementation
- tuning curves
import syde556
theta, x = syde556.sample_around_unit_circle(100)
e = numpy.array([1.0, 0])
J = 0.2*numpy.dot(x.T, e)+1.5
plot(theta*180/numpy.pi, syde556.lif(J))
xlabel('angle')
ylabel('firing rate')
xlim(-180, 180)
show()
Does it match empirical data?
- when tuning curves are plotted just considering $\theta$, they are fit by $a_i=b_0+b_1cos(\theta-\theta_e)$
- where $\theta_e$ is the angle for the encoder $e_i$ and $b_0$ and $b_1$ are constants
Interestingly, Georgopoulos also suggests doing linear decoding:
- $\hat{x}=\sum_i(a_i e_i)$
- This gives a somewhat decent estimate of the direction of movement
- Note that there can be different ways of organizing the representation of a higher dimensional space
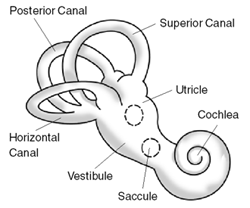
- Here, the neurons respond to angular velocity. This is a 3D vector.
- But, instead of randomly distributing encoders around the 3D space, they are aligned with a major axis
- encoders are chosen from [1,0,0], [-1,0,0], [0,1,0], [0,-1,0], [0,0,1], [0,0,-1]
- This can affect on the representation

Administrative Notes¶
Assignment 1 has been posted
Due: January 29th at dawn (7:42am)
Total marks: 20 (20% of final grade)
Late penalty: 1 mark per day
You can use any programming language you like, but it is recommended that you use a language with a matrix library and graphing capabilities. Two main suggestions are Python and MATLAB.
Tutoring Services
- If you would like more personalized help for the assignments in this course, two of the PhD students in the lab (Xuan Choo and Travis DeWolf) offer tutoring services. They can be contacted at ctntutoring@gmail.com and they charge $20 per half hour (or $15 per person per half hour for groups).