cs1001.py , Tel Aviv University, Fall 2018/19

Exam recitation¶
We went over various questions from previous exams
Takeaways:¶
- The exam is easy, all you have to do is write down the correct answers
- When in doubt, bet on 42
Code for printing several outputs in one cell (not part of the recitation):¶
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
2019AA1: Linked Lists¶
A doubly linked list is similar to a linked list, the difference being that:
- Each node has a next field (pointing forward) and a prev field (pointing backwards)
- The list contains a head field (pointing to the first node) and a tail field (pointing to the last field)
class Node():
def __init__(self, val):
self.value = val
self.next = None
self.prev = None
class DLList():
def __init__(self, lst=None):
self.head = None
self.tail = None
self.len = 0
if lst != None:
for item in lst:
self.insert(item)
def __len__(self):
return self.len
def __repr__(self):
n = len(self)
s = "["
node = self.head
for i in range(n):
s += str(node.value)+", "
node = node.next
if len(s) > 1:
s = s[:-2] + "]"
else:
s += "]"
return s
Implement the insert method. The input is $val$ and $first$ a boolean parameter. If $first==True$ insert at head, else insert at tail.
Runtime and memory usage should be $O(1)$.
The idea is that there are three cases:
- If the list is empty the head and tail should be the new node
- Otherwise, if $first == True$ we should place the new node at the front of the list and change existing head
- Finally, if $first == False$ we should do the same for the tail
class Node():
def __init__(self, val):
self.value = val
self.next = None
self.prev = None
class DLList():
def __init__(self, lst=None):
self.head = None
self.tail = None
self.len = 0
if lst != None:
for item in lst:
self.insert(item)
def __len__(self):
return self.len
def __repr__(self):
n = len(self)
s = "["
node = self.head
for i in range(n):
s += str(node.value)+", "
node = node.next
if len(s) > 1:
s = s[:-2] + "]"
else:
s += "]"
return s
def insert(self, val, first=False):
node = Node(val)
if len(self) == 0:
self.head = self.tail = node
elif first:
tmp = self.head
self.head = node
self.head.next = tmp
tmp.prev = self.head
else:
tmp = self.tail
self.tail = node
self.tail.prev = tmp
tmp.next = self.tail
self.len += 1
Implement the rotate method. Given $0 \leq k < n$, the $i$th node of the list will change place and become the $(i+k)~\%~n$ node.
Runtime should be $O(\textrm{min}(k, n-k))$, memory usage should be $O(\log n)$ and the method should work in place.
class Node():
def __init__(self, val):
self.value = val
self.next = None
self.prev = None
class DLList():
def __init__(self, lst=None):
self.head = None
self.tail = None
self.len = 0
if lst != None:
for item in lst:
self.insert(item)
def __len__(self):
return self.len
def __repr__(self):
n = len(self)
s = "["
node = self.head
for i in range(n):
s += str(node.value)+", "
node = node.next
if len(s) > 1:
s = s[:-2] + "]"
else:
s += "]"
return s
def insert(self, val, first=False):
node = Node(val)
if len(self) == 0:
self.head = self.tail = node
elif first:
tmp = self.head
self.head = node
self.head.next = tmp
tmp.prev = self.head
else:
tmp = self.tail
self.tail = node
self.tail.prev = tmp
tmp.next = self.tail
self.len += 1
def rotate(self, k):
fwd = True
shift = k
if k > len(self) - k:
shift = len(self) - k
fwd = False
self.head.prev = self.tail
self.tail.next = self.head
node = self.head
for i in range(shift):
if fwd:
node = node.prev
else:
node = node.next
self.head = node
self.tail = node.prev
self.head.prev = None
self.tail.next = None
Testing¶
L = DLList([i for i in range(10)])
print(L)
L.rotate(2)
print(L)
2018AA5: Rotating trees¶
Given two BSTs $T,S$ we say that $T$ and $S$ are equivalent if they are the same up to a sequence of switching between left and right sons of some of the nodes in the trees.
The following trees are equivalent:
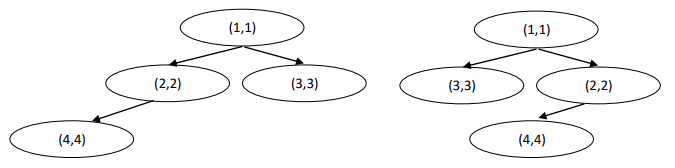
But they are not equivalent to this tree:
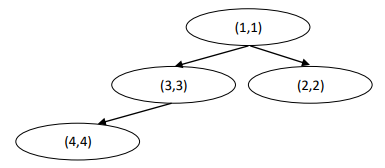
Implement $equiv(r1, r2)$ which gets two root nodes $r1, r2$ and return $True$ iff they represent roots of equivalent trees. The function should be recursive.
The idea is:
- Two leaves are equivalent if their key and value are equivalent
- Two trees are equivalent if:
- Their roots agree on their keys and values
- Their left sons $L1, L2$ and right sons $R1,R2$ are equivalent, or $L1, R2$ and $L2, R1$ are equivlanet
class Tree_node():
def __init__(self, key, val):
self.key = key
self.val = val
self.left = None
self.right = None
def __repr__(self):
return "(" + str(self.key) + ":" + str(self.val) + ")"
def __eq__(self,other):
if other==None:
return False
if self.key==other.key and self.val==other.val:
return True
else:
return False
class Binary_search_tree():
def __init__(self):
self.root = None
def __repr__(self): #no need to understand the implementation of this one
out = ""
for row in printree(self.root): #need printree.py file
out = out + row + "\n"
return out
def lookup(self, key):
''' return node with key, uses recursion '''
def lookup_rec(node, key):
if node == None:
return None
elif key == node.key:
return node
elif key < node.key:
return lookup_rec(node.left, key)
else:
return lookup_rec(node.right, key)
return lookup_rec(self.root, key)
def insert(self, key, val):
''' insert node with key,val into tree, uses recursion '''
def insert_rec(node, key, val):
if key == node.key:
node.val = val # update the val for this key
elif key < node.key:
if node.left == None:
node.left = Tree_node(key, val)
else:
insert_rec(node.left, key, val)
else: #key > node.key:
if node.right == None:
node.right = Tree_node(key, val)
else:
insert_rec(node.right, key, val)
return
if self.root == None: #empty tree
self.root = Tree_node(key, val)
else:
insert_rec(self.root, key, val)
def equiv(node1, node2):
if node1 == node2 == None:
return True
if node1 == None or node2 == None or node1 != node2:
return False
no_switch = equiv(node1.left, node2.left) and equiv(node1.right, node2.right)
switch = equiv(node1.left, node2.right) and equiv(node1.right, node2.left)
return switch or no_switch
Testing¶
T1 = Binary_search_tree()
T1.insert(1,1)
T1.root.left = Tree_node(2,2)
T1.root.right = Tree_node(3,3)
T1.root.left.left = Tree_node(4,4)
T2 = Binary_search_tree()
T2.insert(1,1)
T2.root.left = Tree_node(3,3)
T2.root.right = Tree_node(2,2)
T2.root.right.left = Tree_node(4,4)
T3 = Binary_search_tree()
T3.insert(1,1)
T3.root.left = Tree_node(3,3)
T3.root.right = Tree_node(2,2)
T3.root.left.left = Tree_node(4,4)
equiv(T1.root,T2.root)
equiv(T1.root,T3.root)
#k = Tree_node(1,1)
#p = Tree_node(1,1)
#k == p
Can memoization help? Not really, since subtrees can be disjoint, we will never reach a tree we've already examined.
Next, given two roots of $T1,T2$ determine if there exists a non-empty subtree of $T1$ equivalent to a subtree of $T2$.
The idea
- If the two roots are equivalent (and not empty) we are done
- If one of the roots is $None$, we are done
- Otherwise:
- There may be a subtree of $T2$ equivalent to $T1$
- Or a subtree of $T1$ equivalent to $T2$
def subequiv(node1, node2):
if equiv(node1, node2) and node1 != None:
return True
if node1 == None or node2 == None:
return False
t1_stays = subequiv(node1, node2.left) or subequiv(node1, node2.right)
t2_stays = subequiv(node1.left, node2) or subequiv(node1.right, node2)
return t1_stays or t2_stays
subequiv(T1.root,T2.root)
T4 = Binary_search_tree()
T4.insert(100,100)
T4.root.left = T2.root
subequiv(T4.root, T2.root)
# Since they share leaves
subequiv(T2.root, T3.root)
2018BB5: Hashing¶
For each of the following hash functions for tuples give 2 tuples of integers of length $\geq 3$ (same length for both tuples) that collide.
Possible solutions:
- Since $hash1$ is dependant on values and parities we can simply mix lists while maintaining parity of positions, e.g.: $$(3, 2, 5), (5, 2, 3)$$
- For $hash2$ if the tuples have length $3$ then $hash2(t) = t[0] + 2t[1]+4t[2]$. We can take any $t1$ and place all the weight of $t2$ on the first entry, e.g.: $$(1,1,1), (7,0,0)$$
- For $hash3$, each entry is mapped to its integer value when represented in binary (e.g. - $5 \to 101$). We can get the value of $4 \to 100$ by summing 10 entries of $2 \to 10$, so a possible solution is (note that this is not proper python code):
hash1 = lambda t : sum([(-1)**i * t[i] for i in range(len(t))])
hash2 = lambda t : sum([2**i * t[i] for i in range(len(t))])
hash3 = lambda t : sum(int(bin(t[i])[2:]) for i in range(len(t)))
hash1((3,2,5))
hash1((5,2,3))
hash2((1,1,1))
hash2((7,0,0))
hash3([2 for i in range(10)])
hash3([4] + [0 for i in range(9)])
Given a list $L$ of $n$ tuples of length $2$ we say that $L$ is symmetric if $(a,b) \in L \implies (b,a) \in L$.
Implement $issym$ which gets $L$ as input and returns $True$ iff $L$ is symmetric. The function should run in time $O(n)$ on average.
The idea: we create a set from $L$ and then simply iterate over $L$ and check if each opposite member is in the set.
def issym(L):
n = len(L)
s = set(L)
for i in range(n):
(a,b) = L[i]
if (b,a) not in s:
return False
return True
issym([(1,2), (2,1), (3,3)])
issym([(1,2), (2,1), (3,3), (4,3)])
2017AA2: Profit¶
Given $n$ and a list of integers $values$ of length $n$, we we will think of a landlord that has an apartment of size $n$ square meters. The landlord can divide his apartment into smaller subapartments and an apartment of size $k \leq n$ will yield a rent of $value[k-1]$ dollars.
E.g., for $n = 4, values=[1,5,8,9]$ we can have:
- One apartment of size $4$ renting at $9$ dollars
- Two apartments of size $1$ and one of size $2$ renting at $1+1+5=7$ dollars
- And so on...
Our goal is to find a partition which maximizes the landlords profit. Our solution needs to be recursive and use no loops.
The idea:
- If we don't have any space, or we don't have any partitions available, we make 0 dollars
- If we have 1 meter, we make $value[0]$
- Otherwise, say the length of $len(value)$ is $i$:
- If we can make an apartment of size $i$, i.e. $i \leq size$ then we profit $value[i-1]$ and we need to split $size - i$ meters
- Otherwise, we can shorten the length of $len(value)$ to $i-1$ and we still need to split $size$
- We compute both of the above and take the max between them
def profit(value, size):
n = len(value)
return profit_rec(value, n, size)
def profit_rec(value, i, size):
if size == 0 or i == 0:
return 0
if size == 1:
return value[0]
with_last = 0
if i <= size:
with_last = profit_rec(value, i, size - i)+value[i-1]
without_last = profit_rec(value, i - 1, size)
return max(with_last, without_last)
profit([1, 5, 8, 9], 4)
profit([2, 3, 7, 8, 9], 5)
2017AB2: Jump¶
Given a list $lst$ of $n$ integers where $lst[0]=0$ we want to get to $lst[n-1]$ by jumping to the right (i.e. - advancing in the list).
We init a counter $cnt=0$ and if we add $lst[i]$ to the counter for every index $i$ we visit.
Implement $jump$ which gets a list as described above and returns the minimal total penalty.
The idea: We must visit $lst[-1]$ and we should visit any index $i$ s.t. $lst[i] < 0$.
def jump(lst):
# Note the range!
return lst[-1] + sum(lst[i] for i in range(len(lst)-1) if lst[i] < 0)
jump([0,4,5,1,2,-3,-5])
jump([0,4,5,1,2,-3,2])
Jump limited - we now get a parameter $max\_jump$ and we can now advance only $1 \leq i \leq max\_jump$ steps in each move.
Implement $jump\_rec$ without splicing.
def jump_lim(lst, max_jump):
return jump_rec(lst, max_jump, 0)
def jump_rec(lst, max_jump, ind):
if ind == len(lst) - 1:
return lst[ind]
cnt = float("inf")
for j in range(1, max_jump + 1):
if ind+j < len(lst):
res = jump_rec(lst, max_jump, ind+j) + lst[ind]
if res < cnt:
cnt = res
return cnt
jump_lim([0,4,5,1,2,-3,2], 100)
jump_lim([0, 2, 2, 0, 4], 3)
Add memoization:
def jump_lim(lst, max_jump):
d = {}
return jump_rec_mem(lst, max_jump, 0, d)
def jump_rec_mem(lst, max_jump, ind, d):
if ind == len(lst) - 1:
return lst[ind]
if ind in d:
return d[ind]
cnt = float("inf")
for j in range(1, max_jump + 1):
if ind+j < len(lst):
res = jump_rec_mem(lst, max_jump, ind+j, d) + lst[ind]
if res < cnt:
cnt = res
d[ind] = cnt
return cnt
jump_lim([0,4,5,1,2,-3,2], 100)
jump_lim([0, 2, 2, 0, 4], 3)
2017BA4b: Rotated strings¶
We say that two strings of lengthh $n$, $s,t$ are rotated if there exists and $0 \leq i \leq n$ such that: $$s == t[i:n] + t[0:i]$$
I.e., $introtocs$ is a rotation of $tocsintro$ and of $rotocsint$ but not of $introcsto$.
Implement $is_rot$ which gets two strings and return $True$ iff they are rotated.
The function should work in $O(n)$ and is allowed a small chance of error.
Use $fingerprint, fingerprint\_text$ we've seen when discussing KR.
def is_rot(s, t):
n = len(s)
if n != len(t):
return False
fp = fingerprint(s)
t = t+t
fp_list = substring_fingerprints(t, n)
for i in range(n):
if fp == fp_list[i]:
return True
return False
def fingerprint(string, basis=2**16, r=2**32-3):
""" used to computes karp-rabin fingerprint of the pattern
and of the first substring in the text
employs Horner method (modulo r) """
s = 0
for ch in string:
s = (s*basis + ord(ch)) % r # Horner
return s
def substring_fingerprints(string, m, basis=2**16, r=2**32-3):
""" return a list of all fingerprints of size m windows in string """
fp_list = []
b_power = pow(basis, m-1, r)
# compute first fingerprint
fp_list.append(fingerprint(string[0:m], basis, r))
# compute f_list[s], based on f_list[s-1]
for s in range(1,len(string)-m+1): # O(n-m-1), each iteration O(1)
next_fingerprint = \
((fp_list[s-1] - ord(string[s-1])*b_power) * basis \
+ ord(string[s+m-1])) % r
fp_list.append(next_fingerprint)
return fp_list
is_rot("introtocs", "introtocs")
is_rot("introtocs", "tocsintro")
is_rot("introtocs", "introtosc")
2019AB2: Matching strings¶
Given a list of strings $strlst$ and a string $word$ we say we can construct $word$ from $strlst$ if we can pick at most 1 char from each string in the list that yield $word$.
For example, we can construct "Raz" from $["abc", "FOR", "buzz"]$ and also from $["abc", "FOR", "aaa", "buzz", "hello"]$ but not from $["az", "FOR", "jkl"]$
Implement the recursive $construct\_rec$. The idea is that we maintain an index $j$ s.t. we need to construct $word[j:]$ from the list of strings.
- If $j==len(word)$ we are done.
- Otherwise, we go over the list, for each string we check if it contains $word[j]$ and if so we recurse on $j+1$ and ommit that string from the list
- If we exit the loop without success, we return $False$
def construct(str_list, word):
if len(str_list) < len(word):
return False
return construct_rec(str_list, word, 0)
def construct_rec(str_list, word, j):
if j == len(word):
return True
for i in range(len(str_list)):
if word[j] in str_list[i]:
if construct_rec(str_list[:i]+str_list[i+1:], word, j+1):
return True
return False
construct(["abc", "FOR", "buzz"], "Raz")
construct(["az", "FOR", "jkl"], "Raz")
construct(["az", "FOR", "hello","a"], "Raz")
Now we need to solve a variant where the order of the strings we take must agree with the order of characters in $word$.
E.g., now we can no longer construct "Raz" from $["abc", "FOR", "buzz"]$ but we can from $["FOR", "abc", "jkl", "buzz"]$.
The new solution should run in time $O(n)$ where $n$ is the length fo the string list.
The idea: we can now be greedy. Whenever we can take a certain string we should, because we will not be able to take it from characters later on.
def construct_order(str_list, word):
i = 0
j = 0
while i < len(word) and j < len(str_list):
if word[i] in str_list[j]:
i += 1
j += 1
if i == len(word):
return True
return False
construct_order(["abc", "FOR", "buzz"], "Raz")
construct_order(["FOR", "abc", "buzz"], "Raz")