Sageでグラフを再現してみよう:データ解析のための統計モデリング入門第10章¶
この企画は、雑誌や教科書にでているグラフをSageで再現し、 グラフの意味を理解すると共にSageの使い方をマスターすることを目的としています。
前回に続き、 データ解析のための統計モデリング入門 (以下、久保本と書きます)の第10章の例題をSageを使って再現してみます。
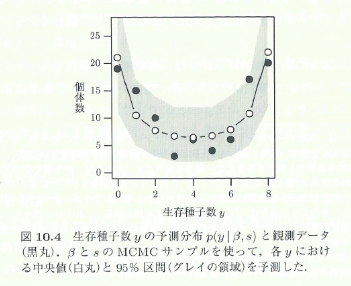
今回の目標は、図10.4です。
数式処理システムSageのノートブックは、計算結果を表示するだけではなく、実際に動かすことができるの大きな特徴です。 この機会にSageを分析に活用してみてはいかがでしょうか。
前準備¶
今回使用するpyjagsがSageの環境では動作しないため、kernelはPython 2を使用します。
最初に必要なライブラリーやパッケージをロードしておきます。sage_util.py, RUtil.pyはloadの代わりにexecを使用して読み込みます。
%%HTML
<link rel="stylesheet" type="text/css" href="css/sage_table_form.css">
# python用のパッケージ
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# statsmodelsを使ってglmを計算します
import statsmodels.formula.api as smf
import statsmodels.api as sm
from scipy.stats.stats import pearsonr
# jags用パッケージ
import pyjags
%matplotlib inline
# jupyter用のdisplayメソッド
from IPython.display import display, Latex, HTML, Math, JSON
# sageユーティリティ
exec(open('script/sage_util.py').read())
# Rユーティリティ
exec(open('script/RUtil.py').read())
# 乱数のシードをセット
np.random.seed(101)
d = pd.read_csv('http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/data7a.csv')
# データのカラムを知る。連番idと生存種子数yからデータであることが分かる
d.head()
| id | y | |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 2 | 2 |
| 2 | 3 | 7 |
| 3 | 4 | 8 |
| 4 | 5 | 1 |
# RのsummaryのようにPandasのDataFrameの情報を出力するには、describeを使用
print "分散=", d.y.var()
d.describe()
分散= 9.92838383838
| id | y | |
|---|---|---|
| count | 100.000000 | 100.000000 |
| mean | 50.500000 | 4.030000 |
| std | 29.011492 | 3.150934 |
| min | 1.000000 | 0.000000 |
| 25% | 25.750000 | 1.000000 |
| 50% | 50.500000 | 4.000000 |
| 75% | 75.250000 | 7.000000 |
| max | 100.000000 | 8.000000 |
# 生存種子数yのヒストグラムと確率密度分布をプロット
sns.distplot(d.y, bins=9)
plt.show()
最尤推定¶
statmodelsのGLMを使って二項分布の最尤推定をします。
求まった切片(0.015)から、qの最尤推定値は以下の様に求まります。 $$ \hat{q} = \frac{1}{1 + exp(-0.015)} = 0.504 $$
二項分布の分散は、$Nqp = 2.0$ですが、データの分散は9.93で過分散となっています。
# statmodelsのGLMを使って解析する
# N-yのカラムを追加
N = 8
d['NmY'] = N - d.y
fit = smf.glm('y + NmY ~ 1', data=d, family=sm.families.Binomial()).fit()
fit.summary2()
| Model: | GLM | AIC: | 763.9388 |
| Link Function: | logit | BIC: | 175.5773 |
| Dependent Variable: | ['y', 'NmY'] | Log-Likelihood: | -380.97 |
| Date: | 2016-08-21 07:29 | LL-Null: | -380.97 |
| No. Observations: | 100 | Deviance: | 631.49 |
| Df Model: | 0 | Pearson chi2: | 491. |
| Df Residuals: | 99 | Scale: | 1.0000 |
| Method: | IRLS |
| Coef. | Std.Err. | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.0150 | 0.0707 | 0.2121 | 0.8320 | -0.1236 | 0.1536 |
# statmodelsの解析結果を使って生存率qを求める
q = 1/(1+np.exp(-0.015)); q
0.50374992968908194
# 二項分布の分散=Nqp
N*q*(1-q)
1.9998875042186155
from math import factorial as fac
def binomial(x, y):
try:
binom = fac(x) // fac(y) // fac(x - y)
except ValueError:
binom = 0
return binom
# 二項分布を定義
def _p(q, y, N):
return binomial(N, y)*q**y*(1-q)**(N-y)
Y = range(9)
q = 0.504
N=8
prob = [_p(q, y, N)*100 for y in Y]
df = pd.DataFrame(zip(Y, prob), columns = ['Y', 'prob'])
ax = d.y.hist(bins=9)
df.plot(kind='scatter', x = 'Y', y='prob', color='red', zorder=2, ax=ax)
plt.show()
階層ベイズモデルの推定・予測¶
二項分布との乖離を生んだのは個体差$r_i$だと仮定して階層ベイズモデルを作成します。
以下に久保本の10.3.1のモデルを示します。jagsではWinBugsのモデルがほぼそのまま使えるのでとても便利です。
- 個体差の標準偏差sは、[0..10000]の一様分布の無情報事前分布から推定
- 個体差$r_i$は、標準偏差sの正規分布からサンプリング
- logistic関数の$q_i = \beta + r+i$から計算し、$q_i$とsから二項分布をサンプリング
N=len(d.y)
code = '''
model {
for (i in 1:N) {
Y[i] ~ dbin(q[i], 8) # 二項分布
logit(q[i]) <- beta + r[i] # 生存率
}
beta ~ dnorm(0, 1.0E-4) # 無情報事前分布
for (i in 1:N) {
r[i] ~ dnorm(0, tau) # 階層事前分布
}
tau <- 1 / (s * s) # tau は分散の逆数
s ~ dunif(0, 1.0E+4) # 無情報事前分布
}
'''
事前サンプリングのデフォルト 1000では、$\beta$がばらついたので、adapt=3000としてモデルを作成しました。
model = pyjags.Model(code, data=dict(Y=d.y, N=N), chains=3, adapt=3000)
adapting: iterations 1374 of 9000, elapsed 0:00:01, remaining 0:00:04 adapting: iterations 3180 of 9000, elapsed 0:00:02, remaining 0:00:03 adapting: iterations 5016 of 9000, elapsed 0:00:03, remaining 0:00:02 adapting: iterations 6870 of 9000, elapsed 0:00:04, remaining 0:00:01 adapting: iterations 8730 of 9000, elapsed 0:00:05, remaining 0:00:00 adapting: iterations 9000 of 9000, elapsed 0:00:05, remaining 0:00:00
samples = model.sample(500, vars=['beta', 's'])
sampling: iterations 1320 of 1500, elapsed 0:00:01, remaining 0:00:00 sampling: iterations 1500 of 1500, elapsed 0:00:01, remaining 0:00:00
サンプリング結果の可視化¶
計算された$\beta$とsを可視化してみましょう。
# betaの可視化
df_beta = pd.DataFrame(samples['beta'][0], columns=['ch1', 'ch2', 'ch3'])
df_beta.plot()
plt.show()
sns.distplot(df_beta.values.flatten())
plt.show()
print np.median(df_beta.values.flatten()), df_beta.values.flatten().mean()
0.00734923506843 0.0115458634885
# betaの可視化
df_s = pd.DataFrame(samples['s'][0], columns=['ch1', 'ch2', 'ch3'])
df_s.plot()
plt.show()
sns.distplot(df_s.values.flatten())
plt.show()
print np.median(df_s.values.flatten()), df_s.values.flatten().mean()
2.9579209966 2.99092478911
階層ベイズモデルの事後分布の計算¶
ここからは、Sageの数値計算を使って計算します。%load_ext sageでSageの関数を利用可能にします。
生存種子数yの確率分布は、二項分布$p(y\,| \,\beta, r)$と正規分布$p(r \,|\, s)$の無限混合分付であり、以下の様にあらわされます。 $$ p(y\,|\,\beta, s) = \int_{-\infty}^{\infty} p(y\,| \,\beta, r)\,p(r \,|\, s)\, dr $$
# ここからSageの関数を使用します
%load_ext sage
生存種子数yの確率分布をプロット¶
Sageの計算処理を使って、$p(y\,| \,\beta, r)\,p(r \,|\, s)$をプロットしてみます。
# p(y | beta, r)p(r | s)を_rで定義
def _gauss(r, s):
return 1/(sqrt(2*pi)*s)*e^(-r^2/(2*s*s))
def _r(y, beta, r, s):
q = 1/(1+exp(-beta -r))
return _p(q, y, 8)*_gauss(r, s)
# Yを0..8に変えて分布を計算する
r = var('r')
beta_med = np.median(df_beta.values.flatten())
s_med = np.median(df_s.values.flatten())
plts = Graphics()
for y in (0..8):
plts += plot(_r(y, beta_med, r, s_med), [r, -10, 10], figsize=5)
# python2カーネルでsageのGraphicsを表示
Graphics2Html(plts)
$p(y\,| \,\beta, r)\,p(r \,|\, s)$の分布からrを-20から20の範囲で数値積分すれば、y毎の生存種子数yの確率分布が計算できることが分かります。
# 上記確率分布をrについて積分する、数値積分の範囲を上記の図から-20から20とした
def _rInt(y, beta, s):
(s, e) = numerical_integral(lambda r : _r(y, beta, r, s), -20, 20)
return s
y毎の生存種子数yの確率分布に100を掛けて、データのヒストグラムと
prob = [_rInt(y, beta_med, s_med)*100 for y in range(9)]
df = pd.DataFrame(zip(Y, prob), columns = ['Y', 'prob'])
ax = d.y.hist(bins=9)
df.plot(kind='scatter', x = 'Y', y='prob', color='red', zorder=2, ax=ax)
plt.show()