import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (12,8)
# Для кириллицы на графиках
font = {'family': 'Verdana',
'weight': 'normal'}
plt.rc('font', **font)
try:
from ipywidgets import interact, IntSlider, fixed
except ImportError:
print u'Так надо'
Задача классификации¶
На прошлом семинаре мы рассматривали модели регрессии - случай, в котором необходимо было предсказать вещественную переменную $y \in \mathbb{R}^n$ (Стоимость автомобиля, стоимость жилья, размер мозга, объемы продаж и тп.)
В задаче классификации переменная $y$ - содержит метку принадлежности к классу, как, например, это было в задаче с наивным байесом - категорию текстов. Частный случай задачи классификации - бинарная классификация $y = \{-1, 1\}$. Например: является ли клиент банка кредитоспособным, доброкачественная ли опухоль, сообщение - SPAM или HAM?
Спрашивается, почему бы нам не взять, да и построить обычную регрессию на метки класса $y$?
Загрузите данные о кредитовании. Они достаточно сильно анонимизированны и еще не до конца подходят для применения, но сейчас это нам не помешает. Постройте график наблюдений в координатах y и a15
df = pd.read_csv('crx.data',index_col=None)
df.head()
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | b | 30.83 | 0.000 | u | g | w | v | 1.25 | t | t | 1 | f | g | 202.0 | 0 | 1 |
| 1 | a | 58.67 | 4.460 | u | g | q | h | 3.04 | t | t | 6 | f | g | 43.0 | 560 | 1 |
| 2 | a | 24.50 | 0.500 | u | g | q | h | 1.50 | t | f | 0 | f | g | 280.0 | 824 | 1 |
| 3 | b | 27.83 | 1.540 | u | g | w | v | 3.75 | t | t | 5 | t | g | 100.0 | 3 | 1 |
| 4 | b | 20.17 | 5.625 | u | g | w | v | 1.71 | t | f | 0 | f | s | 120.0 | 0 | 1 |
df.plot(x='a15', y='y', kind='scatter')
<matplotlib.axes._subplots.AxesSubplot at 0x10f251450>
Почему бы не обучить по этим данным регрессию, предстказывающую значение $y$? Да потому что это бред не очень корректно!
Немного теории¶
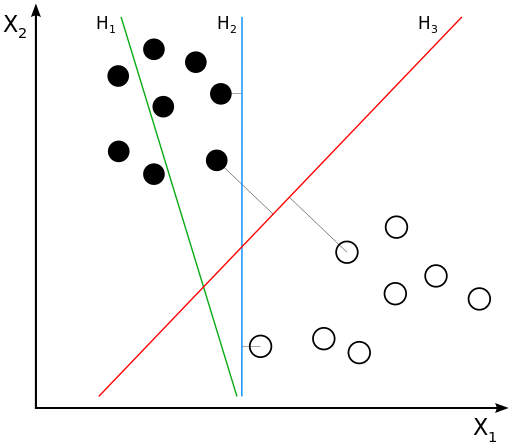
Нам надо найти уравнение прямой (гиперплоскости), которая бы могла разделить два класса ($H_2$ и $H_3$ подходят). В данном случае, уравнение прямой задаётся как: $$g(x) = w_0 + w_1x_1 + w_2x_2 = \langle w, x \rangle = w^\top x$$
- Если $g(x^*) > 0$, то $y^* = \text{'черный'}$
- Если $g(x^*) < 0$, то $y^* = \text{'белый'}$
- Если $g(x^*) = 0$, то мы находимся на линии
- т.е. решающее правило: $y^* = sign(g(x^*))$
Некоторые геометрические особенности
- $\frac{w_0}{||w||}$ - расстояние от начала координат то прямой
- $\frac{|g(x)|}{||w||}$ - степень "уверенности" в классификациий
- Величину $M = y\langle w, x \rangle = y \cdot g(x)$ называют отступом(margin)
Если для какого-то объекта $M \geq 0$, то его классификация выполнена успешно.
Отлично! Значит нам надо просто минимизировать ошибки классификации для всех объектов:
$$L(w) = \sum_i [y^{(i)} \langle w, x^{(i)} \rangle < 0] \rightarrow \min_w$$Проблема в том, что это будет комбинаторная оптимизация. Существуют различные аппроксимации этой функции ошибок:
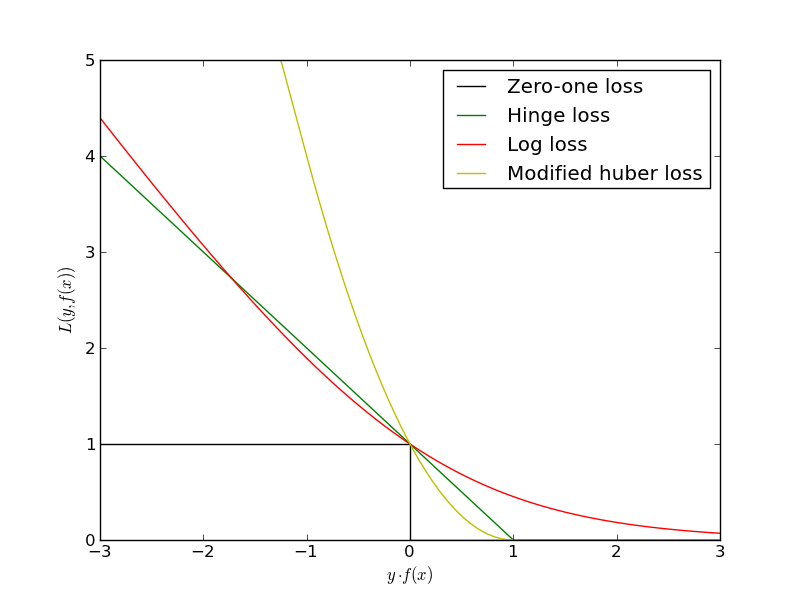
Знакомьтесь - Линейная регрессия!¶
Перед тем как мы начнем, рассмотрим функцию $$\sigma(z) = \frac{1}{1 + exp{(-z)}},$$она называется сигмойда. Постройте данную фукнцию.
# Your code here
def sigmoid(z):
return 1./(1+np.exp(-z))
z = np.arange(-10, 10)
s = sigmoid(z)
plt.plot(z, s)
[<matplotlib.lines.Line2D at 0x10ce595d0>]
Можно несколькими способами представить линейную регрессию. Один из самых простых - вот какой.
Рассмотрим принадлежность к классу $y=\pm1$ некого объекта $x$: $p(y=\pm1 | x,w)$ и выразим её через сигмойду от отступа: $$p(y=\pm1|x,w) = \sigma(y \langle w, x \rangle) $$
А ошибка, которую мы будем минимизировать - логарифмическая:
$$L(w) = -\sum_i \log(\sigma(y^{(i)} \langle w, x^{(i)} \rangle)) \rightarrow \min_w$$История с регуляризацией, мультиколлинеарностью и шкалированием признаков здесь полностью повторяется!
Пример¶
Сгенерируем выборку и опробуем логистическую регрессию
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) + [2, 2],
np.random.randn(20, 2) + [-2, -2]]
y = [-1] * 20 + [1] * 20
fig, ax = plt.subplots(figsize=(7, 7)) ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
from sklearn.linear_model import LogisticRegression
Обучите логистическую регрессию на этих данных и нарисуйте разделяющую гиперплоскость
## Your Code Here
Как сделать нелинейную границу?¶
Рассмотрим набор данных, который в простонародье называют "Бублик".
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=100, shuffle=True, noise = 0.1, factor=0.1)
X = X
plt.scatter(X[:, 0],
X[:, 1],
c=y)
<matplotlib.collections.PathCollection at 0x112dfe0d0>
Очевидно, что классы нельзя разделить линией. Но можно сделать это окружностью! Т.е. разделяющся линия теперь будет задаваться не уравнением прямой $g(x) = w_0 + w_1x_1 + w_2x_2$, а уравнением окружности $c(x) = (x_1 - a)^2 + (x_2 - b)^2 - R^2$.
Выполните преобразование матрицы X, чтобы в ней были столбцы для $x_1$, $x^2_1$, $x_2$, $x^2_2$ и обучите логистическую регрессию
# Your code here
Задача на "реальных" данных¶
Предобработка данных¶
Вновь данные по кредитованию.
Столбец с классом называется y.
Значение $1$ соответствует классу клиентов банка, которым выдали кредит и они его успешно вернули.
Значение $-1$ соответствует клиентам, невыполнившим свои кредитные обязанности.
В банке хотят уметь определять по признакам a1-a15, сможет ли новый клиент вернуть кредит или нет? То есть нам надо обучить классификатор! Обычно, в банках используют скор-карты, но процесс их построения тесно связан с логистической регрессией
Загрузите данные и преобразуйте признаки a1, a9, a10 и a12 из строковых в числовые. В них только 2 возможных значения. Для этого можно использовать функцию DataFrame.replace() в pandas или самое обычное присваивание на соответствующих строках.
В признаках a6, a7 присутствуют "редкие" значение. Найдите их с помощью фунцкии .value_counts() и объедините, присвоив им одно и то же значение, например 'Other'.
Выделите бинарные признаки a1, a9, a10 и a12 в матрицу X_binary
Преобразуйте категориальные признаки a5, a6, a7, a13 с помощью DictVectorizer. Вы должны получить матрицу X_cat.
Нормализуйте количественные признаки a2, a3, a8, a11, a14 и a15 с помощью StandartScaler или вручную. Вы должны получить матрицу X_real.
Матрица X_cat будет sparse-матрицой (разреженной). Преобразуте её в полную матрицу с помощью команд X_cat = X_cat.toarray() или X_cat = X_cat.todence()
Используйте функцию np.concatinate(..) или np.c[..] чтобы сцепить матрицы X_binary, X_cat и X_real
В результате вы должны получить матрицу с преобразованными призанками X и вектор ответов y
Исследование влияния регуляризации¶
В случае с логистичесткой регресии, сложность модели выражается в значениях весов $w_j$ при признаках. Больший вес означает большее влияние признака на результат. В таком случае, давайте добавил штрафное слагаемое в функцию оптимизации для логистической регресии. Самый распространенные из них это:
- Ridge regression
- Lasso regression
$C$ - называется гиперпараметром регуляризации и он задается вручную. Выбирается он с помощью кросс-валидации. Чем больше $С$ - тем меньше влияние регуляризации.
Разделите ваши даннные на обучающую и контрольную выборку в пропорции 70/30 соответственно.
Lasso regression называется так, потому что она осуществляет "отлов" признаков - т.е. незначимые признаки будут иметь нулевые веса в модели, в то время как в Ridge regression - веса будут постепенно падать у всех признаков.
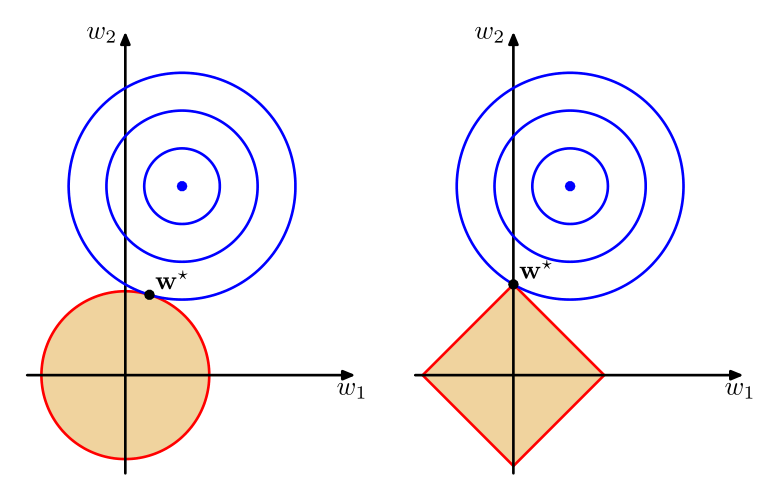
Давайте сравним работу регуляризаторов.
- Разбейте данные на обучающую и валидационную выборки в пропорции 70\30.
- Для $C$ из набора np.logspace(-3, 3, 10) обучите LogisctigRegression c Lasso регуляризацией (
penalty='l1'). На каждой итерации оцените качество (ROC-AUC) на контрольной выборке и запомните полученные коэффициенты модели - На одном графике выведите значение качества в зависимости от параметра
C - На другом графике для каждого признака выведите значение коэффициента в модели в зависимости от параметра
C - Проделайте тоже самое для Ridge регуляризации (
penalty='l2')