Линейная регрессия¶
Шестаков А.В. Майнор по анализу данных - 01/03/2016
Сегодня мы рассмотрим следующие темы:
- Постановка задачи линейной регрессии
- Преобразование переменных и интерпретация
- Переобучение\недообучение, мультиколлинеарность и регуляризация
1. Постановка задачи¶
Дано описание $n$ объектов по $m$ признакам. Обычно оно выражается в виде матрицы размера $n \times m$: $X = [x^{(i)}_j]^{i=1\dots n}_{j=1\dots m} $.<br> ($x^{(i)}_j$ означает $j$-ый признак $i$-го объекта) <br> Дана вещественная зависимая переменная, которая тоже имеет отношение к этим объекам: $y \in \mathbb{R}^n$.
Наша задача, выявить линейную зависимость между признаками в $X$ и значениями в $y$: $$\hat{y} = X\beta \quad \Leftrightarrow \quad \hat{y}^{(i)} = \beta_0 + \beta_1x^{(i)}_1 + \dots$$ То есть необходимо оценить коэффициенты $\beta_i$.
В случае линейной регрессии коэффициенты $\beta_i$ рассчитываются так, чтобы минимизировать сумму квадратов ошибок по всем наблюдениям: $$ L(\beta) = \frac{1}{2n}(\hat{y} - y)^{\top}(\hat{y} - y) = \frac{1}{2n}(X\beta - y)^{\top}(X\beta - y) \rightarrow \min$$ $$ \Updownarrow $$ $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}\sum^{n}_{i=1}(\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{2n}\sum^{n}_{i=1}(\beta_0 + \beta_1x^{(i)}_1 + \dots - y^{(i)})^2 \rightarrow \min $$
Мы уже знаем несколько способов решения этой задачи (Семинар 4):
- Градиентный спуск
- Normal Equations (Проекционные матрицы)
Библиотеки для расчетов¶
Самыми распространенными библиотеками в Python для работы с линейными методами (регрессии и классификации) являются scikit-learn и statmodels. Так как в дальнейшем мы скорее всего будем работать со scikit-learn, то и примеры по большей части будут демонстрироваться именно в нем.
Пример: Стоимость автомобиля¶
Загрузите данные по характеристикам автомобилей Honda Accord. Названия столбцов говорят сами за себя.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.style.use('ggplot')
%matplotlib inline
df = pd.read_csv('http://bit.ly/1gIQs6C')
df.head()
Выберем одну переменную mileage в качестве предиктора, а переменную price в качестве зависимой переменной
y = df.price.values
X = df.mileage.values.reshape(-1,1)
# В последних версиях sklearn начинает ругаться на одномерные данные (когда array.shape = (m,))
# Поэтому с помошщью .reshape(-1,1) мы искусственно добавляем единичную размерность к Х
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model.fit(X, y)
print 'Модель:\nprice = %.2f + (%.2f)*mileage' % (model.intercept_, model.coef_[0])
x = np.linspace(0, max(X), 100)
y_line = model.intercept_ + model.coef_[0]*x
fig, ax = plt.subplots(1, 1, figsize=(10,5))
ax.scatter(X, y)
ax.plot(x, y_line, c='red')
Остатки и меры качества¶
Давайте взглянем на ошибки (остатки)
fig, ax = plt.subplots(1, 2, figsize=(14, 5))
y_hat = model.predict(X)
res = y - y_hat
ax[0].hist(res)
ax[0].set_xlabel('residuals')
ax[0].set_ylabel('counts')
ax[1].scatter(X, res)
ax[1].set_xlabel('mileage')
ax[1].set_ylabel('residuals')
Важно смотреть на остатки.
Во-первых, они должны быть нормально распределены (Теорема Гаусса-Маркова).
Во-вторых, не должно быть ярких зависимостей между значениями признака и остатками.
Посмотрим на меры качества
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import median_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
Можно посчитать простые варианты агрегирования остатков, например:
- $\frac{1}{n} \sum_i |\hat{y}^{(i)}-y^{(i)}|$ - средняя абсолютная ошибка
- $\frac{1}{n} \sum_i (\hat{y}^{(i)}-y^{(i)})^2$ - средняя квадратичная ошибка
print 'Средняя абсолютная ошибка %.2f' % mean_absolute_error(y, y_hat)
print 'Средняя квадратичная ошибка %.2f' % mean_squared_error(y, y_hat)
Можно рассмотреть более сложную меру: коэффициент детерминации $R^2$:
- $TSS = \sum_i (y^{(i)}-\bar{y})^2$ - общая сумма квадратов (total sum of squares)
- $RSS = \sum_i (\hat{y}^{(i)}-y^{(i)})^2$ - сумма квадратов остатков (residual sum of squares)
- $ESS = \sum_i (\hat{y}^{(i)}-\bar{y})^2$ - объясненная сумма квадратов (explained sum of squares)
Для простоты будем считать, что $$TSS = ESS + RSS$$
Тогда Коэффициент детерминации $R^2=1-\frac{RSS}{TSS}$
print 'R^2 %.2f:' % r2_score(y, y_hat)
Тоже самое через statmodels
import statsmodels.api as sm
model = sm.OLS(y, sm.add_constant(X))
results = model.fit()
print(results.summary())
2. Преобразование переменных¶
Нормализация¶
Как мы с вами убедились из ДЗ2, может решить всё) Переход к близким или единым шкалам улучшает сходимость градиентного спуска, уменьшает риск переполнения разрядности чисел, однако приходится жертвовать прямой интерпретируемостью..
Нормализацию обычно проделывают для вещественных признаков.
Нормализация z-score:
- Вычитаем среднее: $x - \bar{x}$
- Делим на стандартное отклонение: $\frac{x - \bar{x}}{std(x)}$
Можно проделать вручную, можно с помошью метода ниже
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
model = LinearRegression(fit_intercept=True)
model.fit(X, y)
print 'Модель:\nprice = %.2f + (%.2f)*mileage`' % (model.intercept_, model.coef_[0])
Номинальная шкала¶
df.head()
Обратим внимание, что в нашем DataFrame есть и другие переменные - год, особенности внешности, количество цилиндров, тип коробки передач. Как учесть их в модели? Иными словами, как их перекодировать, для использование в модели регресии?
Часть из них можно представить в виде так называемых dummy (фиктивных) переменных
from sklearn.feature_extraction import DictVectorizer
cols = df.columns[1:]
dv = DictVectorizer()
dv.fit(df[cols].T.to_dict().values())
X = dv.transform(df[cols].T.to_dict().values())
Давайте поймем, как устроен X
Пример: Стоимость автомобиля - больше переменных!¶
Обратите внимание, что в случае, когда мы добавляем все категории в матрицу X, рассчитывать вес для свободного члена не нужно.
Причиной тому - так называемая Dummy Variable Trap. Матрица $X^\top X$ перестаёт быть обратимой из-за линейной зависимости столбцов (своего рода мультиколлинеарность).
Хотя, даже если поставить fit_intercept=True, sklearn вас даже не остановит...
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
# Выведите значение коэффициента для каждой переменной и проинтерпретируйте их значение
y_hat = model.predict(X)
print 'Средняя абсолютная ошибка %.2f' % mean_absolute_error(y, y_hat)
print 'Средняя квадратичная ошибка %.2f' % mean_squared_error(y, y_hat)
print 'R^2 %.2f:' % r2_score(y, y_hat)
Природа зависимости¶
Далеко не всегда переменные зависят друг от друга именно в том виде, в котором они даны. Никто не запрещает зависимость вида $$\log(y) = \beta_0 + \beta_1\log(x_1)$$ или $$y = \beta_0 + \beta_1\frac{1}{x_1}$$ или $$y = \beta_0 + \beta_1\log(x_1)$$ или $$y = \beta_0 + \beta_1 x_1^2 + \beta_2 x_2^2 + \beta_3 x_1x_2 $$ и т.д.
Не смотря на то, что могут возникать какие-то нелинейные функции - всё это сводится к линейной регрессии (например, о втором пункте, произведите замену $z_1 = \frac{1}{x_1}$)
Пример: Вес тела - мозгов¶
Загрузите данные и информацией о весах мозга и тел различных биологических видов. Вес тела задан в килограммах, вес могза в граммах.
df = pd.read_csv('weights.csv', sep=';', index_col=0)
df.head()
df.plot(x = 'body_w', y='brain_w', kind='scatter')
for k, v in df.iterrows():
plt.annotate(k, v[:2])
# Должно получится что-то несуразное..
Теперь давайте возьмем логарифм от обеих переменных и сонова нарисуем их на графике
# Your Code Here
Постройде линейную регрессию над логарифмами значений. Найдите коэффициенты и проинтерпретируйте их
# Your Code Here
3. Переобучение\недообучение, мультиколлинеарность и регуляризация¶
Одна из важнейших характеристик моделей, будь то линейная регрессия, наивные Байес и др. - их обобщающая способность. Наша задача не построить "идеальную" модель, на имеющихся у нас наблюдениях, которая идеально их будет предсказывать, но и применять эту модель для новых данных.
Ниже приводятся примеры 3х моделей.
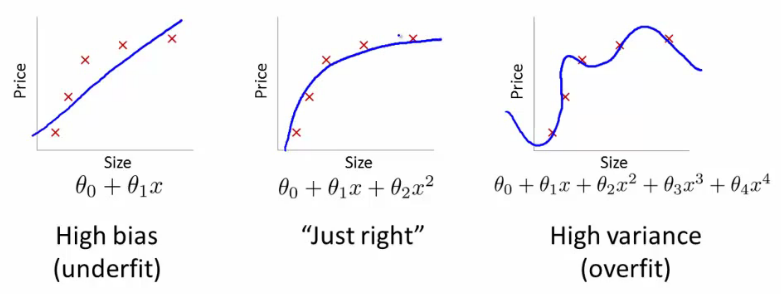 [Andrew's Ng Machine Learning Class - Stanford]
[Andrew's Ng Machine Learning Class - Stanford]
Второй момент, который важен для линейных моделей - мультиколлинеарность. Этот эффект возникает, когда пара предикторов близка к взаимной линейной зависимости (коэффициент корреляции по модулю близок к 1). Из-за этого:
- Матрица $X^{\top} X$ становится плохо обусловленной или необратимой
- Зависимость $y = \beta_0 + \beta_1x_1 + \beta_2x_2$ перестаёт быть одназначной
С этим эффектом можно бороться несколькими способами
- Последовательно добавлять переменные в модель
- Исключать коррелируемые предикторы
Регуляризация¶
В обоих случаях может помочь регуляризация - добавление штрафного слагаемого за сложность модели в функцию потерь. В случае линейной регрессии было: $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}\sum^{n}_{i=1}(\hat{y}^{(i)} - y^{(i)})^2 $$ Стало (Ridge Regularization) $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}[ \sum^{n}_{i=1}(\hat{y}^{(i)} - y^{(i)})^2 + \lambda\sum_{j=1}^{m}\beta_j^2]$$ или (Lasso Regularization) $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}[ \sum^{n}_{i=1}(\hat{y}^{(i)} - y^{(i)})^2 + \lambda\sum_{j=1}^{m}|\beta_j|]$$
# В sklearn эти методы называются так
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge