Методы кластеризации¶
Шестаков А.В. Майнор по анализу данных 24/05/2016
Задача кластеризации - задача выделения групп похожих друг на друга объектов (и интерпретация полученных групп).
Кластеризация - это задача unsupervised learning (обучения без учителя), то есть на вход алгоритму поступают лишь чистые данные и никакой разметки.
Методов кластеризации великое множество, выбор лежит полностью на совести исследователя. Определение метода кластеризации может зависеть от
- Формата исходных данных
- Необходимости в наглядности представления
- Необходимости в интерпретируемости
- Модельных предположений о данных
- ...
K-Means¶
Самый простой и известный метод кластеризации, основным понятием которого является центройд $c_k$ (центр кластера). Критерий минимизации: $$ \min J(C) = \min\limits_{c_k} \sum\limits_k\sum\limits_{x_i\in c_k} ||x_i - c_k||^2 $$ Шаги алгоритма
- Случайно инициализировать центройды
- Отнести точки к ближайшим центройдам (получаем кластеры)
- Перенести центройды в центр получившихся кластеров (поправка к оценке координат центройдов)
- Повторять шаги 1-2 пока критерий не содется\кластеры не изменятся
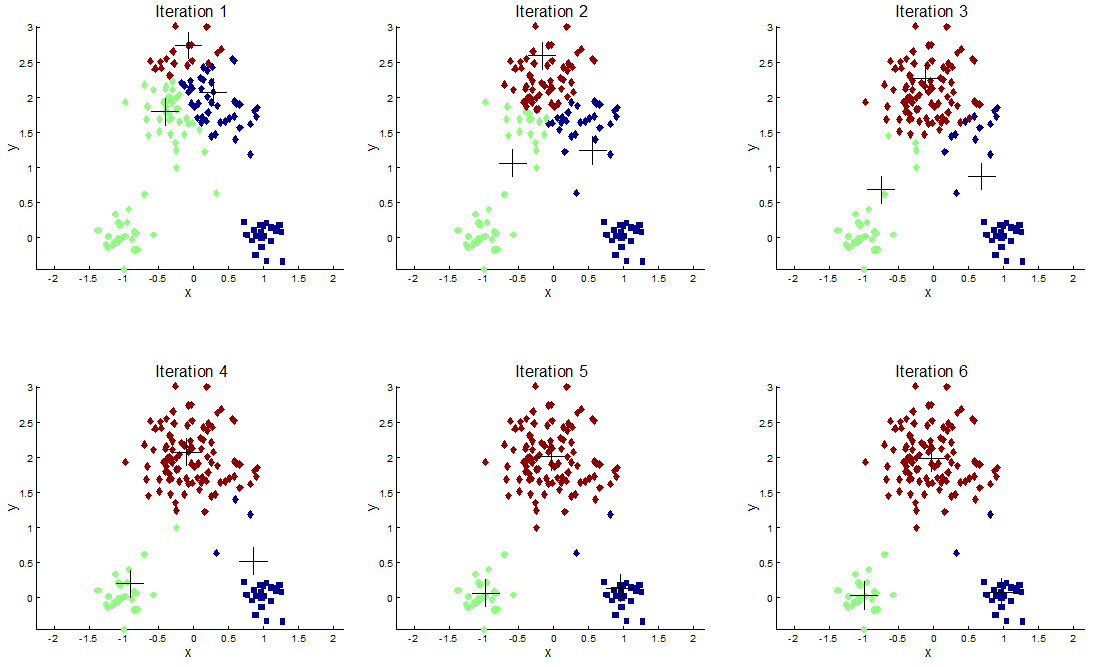
- Какие недостатки сразу бросаются в глаза?
- Как обстоят дела с выбором количества кластеров?
- Необходимо ли нормировать данные?
- Приведите пример данных, которые человек "на глаз" может легко кластеризовать, а k-mean - сделает это неправильно
- Как поменяется алгоритм, если вместо квадрата в $J(C)$ поставить модуль?
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import confusion_matrix
from sklearn.metrics import adjusted_rand_score
%matplotlib inline
X, y = make_blobs(n_samples=1000, n_features=2,
centers=3, random_state=15)
plt.scatter(X[:,0], X[:,1], c=y)
# Применяем k-means
kmeans = KMeans(n_clusters=3)
y_hat = kmeans.fit_predict(X)
plt.scatter(X[:,0], X[:,1], c=y_hat)
Крактически идеально! А если мы слегка изковеркаем данные? Заодно, давайте узнаем, как можно таки измерять качество кластеризации, если у нас есть правдивые метки?
Adjusted Rand Index нам в помощь!
Trans = [[ 0.40834549, -0.43667341],
[-0.10887718, 0.829]]
X_t = X.dot(Trans)
# Your code here
Иерархическая кластеризация¶
В отличие от стандартного k-means, на входе алгоритма иерархической кластеризации лежит матрица попарных расстояний между объектами. Идея (аггломеративной) иерархической кластеризации заключается в постепенном объединении объектов во всё более массивные кластеры.
Вопрос: а как пересчитывать попарные расстояние между кластерами в таком случае?

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
from scipy.cluster.hierarchy import fcluster
# Матрицу признакового описания надо отнормировать
# Your code here
Приятная вещица, связанная с иерархической кластеризацией - дендрограмма!
# Your code here
# Для того, чтобы определить метки кластеров используем fcluster
# Your code here
Смесь гаусовских распределений (GMM)¶
Каждая точка представляется ввиде смести гауссовских распределений:
$$P(x) = \sum\limits_k P(x|c_k) \cdot P(c_k) = \mathcal{N}(x| \mu_k, \Sigma_k)\cdot\pi_k$$В процессе итеративного алгоритма (EM-алгоритм для GMM) определяются параметры \mu_k, \Sigma_k, \pi_k а так же "вклады" каждого распределения в объекты.
- Во-первых, мы получает смягченную кластеризацию
- Во-вторых, ловим чуть более сложные формы кластеров, чем k-means
from sklearn.mixture import GMM
X, y = make_blobs(n_samples=1000, n_features=2,
centers=3, random_state=15)
Trans = [[ 0.40834549, -0.43667341],
[-0.10887718, 0.829]]
X = X.dot(Trans)
plt.scatter(X[:,0], X[:,1], c=y)
# Your code here
import matplotlib as mpl
def make_ellipses(gmm, ax):
for n, color in enumerate('rgb'):
v, w = np.linalg.eigh(gmm._get_covars()[n][:2, :2])
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan2(u[1], u[0])
angle = 180 * angle / np.pi # convert to degrees
v *=9
ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
180 + angle, color=color)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.5)
ax.add_artist(ell)
plt.scatter(X[:,0], X[:,1], c=y_hat)
make_ellipses(gmm, plt.gca())
# Можем посмотреть на параметры получившихся распределений
# Your code here
Задание¶
- Выберите любую (желательно красочную) картинку, подгузите её с помощью
plt.imread() - Выполните компрессию изображения с помощью метода k-means, т.е. задайте некоторе число кластеров, произведите кластеризацию, затем замените соответствующие пиксели на значения центройдов.
# Your code here