Линейные методы классификации¶
Шестаков А.В. Майнор по анализу данных 15/03/2016
Сегодня мы рассмотрим следующие темы
- Задача классификации
- Методы линейной классификации
- Регуляризация линейной регрессии и градиентный спуск
Задача классификации¶
На прошлом семинаре мы рассматривали модели регрессии - случай, в котором необходимо было предсказать вещественную переменную $y \in \mathbb{R}^n$ (Стоимость автомобиля, стоимость жилья, размер мозга, объемы продаж и тп.)
В задаче классификации переменная $y$ - содержит метку принадлежности к классу, как, например, это было в задаче с наивным байесом - категорию текстов. Частный случай задачи классификации - бинарная классификация $y = \{-1, 1\}$. Например: является ли клиент банка кредитоспособным, доброкачественная ли опухоль, сообщение - SPAM или HAM?
Спрашивается, почему бы нам не взять, да и построить обычную регрессию на метки класса $y$?
Загрузите данные о кредитовании. Они достаточно сильно анонимизированны и еще не до конца подходят для применения, но сейчас это нам не помешает. Постройте график наблюдений в координатах y и a15
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
df = pd.read_csv('crx.data',index_col=None)
df.head()
# Your code here
Почему бы не обучить по этим данным регрессию, предстказывающую значение $y$? Да потому что это бред не очень корректно!
Методы линейной классификации¶
Обратимся к слегка идеализированному варианту, линейно разделимой выборке:
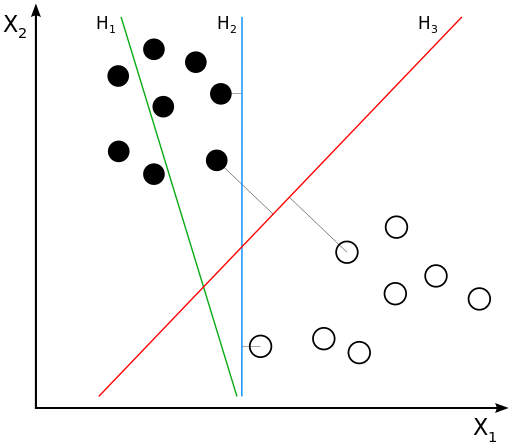
Нам надо найти уравнение прямой (гиперплоскости), которая бы могла разделить два класса ($H_2$ и $H_3$ подходят). В данном случае, уравнение прямой задаётся как: $$g(x) = w_0 + w_1x_1 + w_2x_2 = \langle w, x \rangle = w^\top x$$
- Если $g(x^*) > 0$, то $y^* = \text{'черный'}$
- Если $g(x^*) < 0$, то $y^* = \text{'белый'}$
- Если $g(x^*) = 0$, то мы находимся на линии
- т.е. решающее правило: $y^* = sign(g(x^*))$
Некоторые геометрические особенности
- $\frac{w_0}{||w||}$ - расстояние от начала координат то прямой
- $\frac{|g(x)|}{||w||}$ - степень "уверенности" в классификациий
- Величину $M = y\langle w, x \rangle = y \cdot g(x)$ называют отступом(margin)
Если для какого-то объекта $M \geq 0$, то его классификация выполнена успешно.
Отлично! Значит нам надо просто минимизировать ошибки классификации для всех объектов:
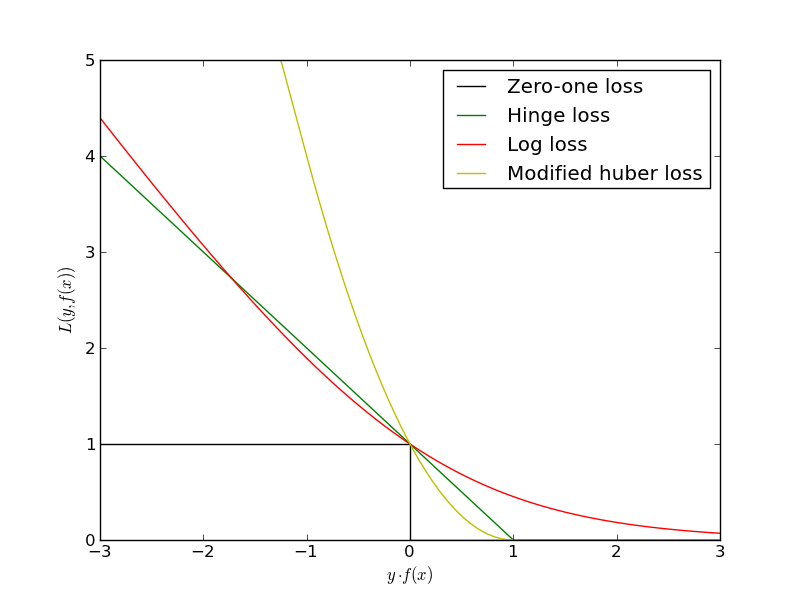
$$L(w) = \sum_i [y^{(i)} \langle w, x^{(i)} \rangle < 0] \rightarrow \min_w$$Проблема в том, что это будет комбинаторная оптимизация. Существуют различные аппроксимации этой функции ошибок:
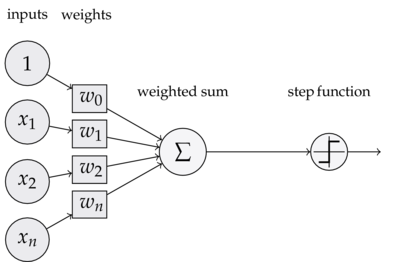
Знакомьтесь - Перцептрон!¶
Это самая простая модель человеческой нейронной сети. В ней есть входы, которые взвешиваются и суммируются. Затем взвешенная сумма проходит через некую функцию активации (в данном случае $sign(\cdot)$).
Перцептрон можно использовать для классификации.
Существует итерационный алгоритм, который корректирует веса $w_0 \cdots w_n$ до тех пор, пока ошибки имею место быть:
Randomly initialize weights: w=(w_0, \dots, w_d)
Until no errors on train set:
for i in xrange(N):
if y_i * w.T * x_i < 0:
w = w + alpha * y_i * x_i
Этот алгоритм гарантированно сходится для линейно разделимой выборки. А если это не наш случай?
Знакомьтесь - Логистическая регрессия!¶
Перед тем как мы начнем, рассмотрим функцию $$\sigma(z) = \frac{1}{1 + exp{(-z)}},$$она называется сигмойда. Постройте данную фукнцию.
# Your code here
Можно несколькими способами представить линейную регрессию. Один из самых простых - вот какой.
Рассмотрим принадлежность к классу $y=\pm1$ некого объекта $x$: $p(y=\pm1 | x,w)$ и выразим её через сигмойду от отступа: $$p(y=\pm1|x,w) = \sigma(y \langle w, x \rangle) $$
Будем максимизировать правдоподобие $$\mathcal{L}(w) = \prod_i p(y^{(i)}|x^{(i)},w) \rightarrow \max_w$$ Возьмем от этого логарифм и поставим минус - получится минимизация логарифмической функции потерь:
$$L(w) = -\sum_i \log(\sigma(y^{(i)} \langle w, x^{(i)} \rangle)) \rightarrow \min_w$$Посчитаем градиент этой функции потерь по $w$:
$$ \frac{\partial L(w)}{\partial w} = \dots$$История с градиентным спуском, регуляризацией, мультиколлинеарностью и шкалированием признаков здесь полностью повторяется!
Сгенерируем выборку и применим к ней линейную регрессию
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) + [2, 2],
np.random.randn(20, 2) + [-2, -2]]
y = [-1] * 20 + [1] * 20
fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter(X[:, 0],
X[:, 1],
c=y,
cmap=plt.cm.Paired)
from sklearn.linear_model import LogisticRegression
Обучите LogisticRegression() на данных X и y, изобразите разделяющую прямую
model = LogisticRegression()
## Your code here