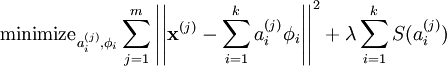Data Driven Modeling¶
### PhD seminar series at Chair for Computer Aided Architectural Design (CAAD), ETH Zurich
Topics to be discussed¶
- Linear Algebra
- Linear Transformations
- PCA
- Extensions to PCA
In [69]:
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
pd.__version__
import sys
from scipy import stats
%matplotlib inline
from bokeh.models import CustomJS, ColumnDataSource, Slider,TextInput
from bokeh.models import TapTool, CustomJS, ColumnDataSource
from bokeh.layouts import column
from bokeh.layouts import gridplot
from bokeh.models import ColumnDataSource
from bokeh.layouts import gridplot
from bokeh.plotting import figure
from bokeh.io import output_notebook, show
from bokeh.plotting import Figure, output_file, show
from bokeh.layouts import widgetbox
from bokeh.models.widgets import Slider
from bokeh.io import push_notebook
from bokeh.io import show
from bokeh.models import (
ColumnDataSource,
HoverTool,
LinearColorMapper,
BasicTicker,
PrintfTickFormatter,
ColorBar,
)
output_notebook()
from bokeh.layouts import column
from bokeh.models import CustomJS, ColumnDataSource, Slider
from bokeh.plotting import Figure, output_file, show
Some Basic notions in Linear Algebra¶
A vector (or a point in n dimensional space)¶
In [31]:
x = np.asarray([[2,2]])
x.shape
Out[31]:
(1, 2)
In [32]:
plt.plot([0,x[0,0]],[0,x[0,1]],'-or',markersize=20)
plt.xlim(0,3)
plt.ylim(0,3)
Out[32]:
(0, 3)
Matrix Operation¶
Special Linear transformers¶
In [33]:
#rotation 90 degrees
A =np.asarray([[0,-1],[1,0]])
y = x.dot(A)
y.shape
Out[33]:
(1, 2)
In [34]:
fig = plt.figure(figsize=(5,5))
plt.plot([0,x[0,0]],[0,x[0,1]],'-or')
plt.plot([0,y[0,0]],[0,y[0,1]],'-ob')
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.axis('equal');
In [35]:
#rotation t degrees
t = np.pi/4.
A =np.asarray([[np.cos(t),-1*np.sin(t)],[np.sin(t),np.cos(t)]])
y = x.dot(A)
x.shape
Out[35]:
(1, 2)
In [36]:
fig = plt.figure(figsize=(5,5))
plt.plot([0,x[0,0]],[0,x[0,1]],'-or')
plt.plot([0,y[0,0]],[0,y[0,1]],'-ob')
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.axis('equal');
In [37]:
A =np.asarray([[1,1],[1,0]])
y = x.dot(A)
y.shape
fig = plt.figure(figsize=(5,5))
plt.plot([0,x[0,0]],[0,x[0,1]],'-or')
plt.plot([0,y[0,0]],[0,y[0,1]],'-ob')
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.axis('equal');
In [38]:
#rotation t degrees
t = 1*np.pi/2.
A =np.asarray([[np.cos(t),-1*np.sin(t)],[np.sin(t),np.cos(t)]])
N = 100
x1= np.random.uniform(low=0,high=10,size=N)[:,np.newaxis]
x1= np.random.normal(loc=0,scale=3,size=N)[:,np.newaxis]
x2 = 1*x1 + np.random.normal(loc=0.0, scale=1.7, size=N)[:,np.newaxis]
X = np.concatenate((x1,x2),axis=1)
Y = X.dot(A)
fig = plt.figure(figsize=(7,7))
ax1= plt.subplot(111)
plt.plot(X[:,0],X[:,1],'.r',markersize=10,alpha=.4 );
ax1= plt.subplot(111)
plt.plot(Y[:,0],Y[:,1],'.b',markersize=10,alpha=.4 );
plt.grid();
plt.axis('equal');
Fiboonatchi series¶
$$ x_0 = 0 $$$$ x_1 = 1 $$$$ xtp_2 = xtp_1 + xt $$In [39]:
xtp_1=1
xt = 0
for i in range(10):
xtp_2 = xtp_1 + xt
xt = xtp_1
xtp_1 = xtp_2
print xtp_2
1 2 3 5 8 13 21 34 55 89
In Matrix Form¶
If we write down these two equations: $$ xtp_2 = xtp_1 + xt $$ $$xtp_1 = xtp_1$$
Then, we have a system of equation as follows
$$[xtp_2, xtp_1] = [xtp_1, xt][[1,1],[1,0]]$$In [40]:
F =np.asarray([[1,1],[1,0]])
print(np.matrix(F))
[[1 1] [1 0]]
In [41]:
xtp_1=1
xt = 0
X = np.asarray([xtp_1,xt])
print X[0]
for i in range(10):
X = X.dot(F)
print X[0]
1 1 2 3 5 8 13 21 34 55 89
In [13]:
M =np.asarray([[.9,.1],[.5,.5]])
print(np.matrix(M))
print
x = np.asarray([0,1])
print x
for i in range(20):
x = x.dot(M)
print x
print x
[[ 0.9 0.1] [ 0.5 0.5]] [0 1] [ 0.5 0.5] [ 0.7 0.3] [ 0.78 0.22] [ 0.812 0.188] [ 0.8248 0.1752] [ 0.82992 0.17008] [ 0.831968 0.168032] [ 0.8327872 0.1672128] [ 0.83311488 0.16688512] [ 0.83324595 0.16675405] [ 0.83329838 0.16670162] [ 0.83331935 0.16668065] [ 0.83332774 0.16667226] [ 0.8333311 0.1666689] [ 0.83333244 0.16666756] [ 0.83333298 0.16666702] [ 0.83333319 0.16666681] [ 0.83333328 0.16666672] [ 0.83333331 0.16666669] [ 0.83333332 0.16666668] [ 0.83333332 0.16666668]
But in machine learning we are usually interested in designing or learning certain operators¶
In [42]:
N = 500
x1= np.random.uniform(low=0,high=10,size=N)[:,np.newaxis]
x1= np.random.normal(loc=0,scale=3,size=N)[:,np.newaxis]
x2 = 1*x1 + np.random.normal(loc=0.0, scale=2.7, size=N)[:,np.newaxis]
X = np.concatenate((x1,x2),axis=1)
fig = plt.figure(figsize=(7,7))
ax1= plt.subplot(111)
plt.plot(X[:,0],X[:,1],'.r',markersize=10,alpha=.4 );
plt.grid();
plt.axis('equal');
In [43]:
# look how dependent are the two original dimensions
# X_trans = X.dot(PCs[:,:5])
DF = pd.DataFrame(data=X)
from pandas.tools.plotting import scatter_matrix
scatter_matrix(DF, alpha=0.2, figsize=(6, 6), diagonal='hist');
In [44]:
# Normalizing it around 0
X = X-np.mean(X,axis=0)
XTX = X.T.dot(X)/(X.shape[0]-1)
np.around(XTX,decimals=3)
# This is a multiplication of the covariance matrix we discussed before
Out[44]:
array([[ 9.474, 9.611],
[ 9.611, 16.868]])
In [45]:
COVX = np.cov(X.T)
np.around(COVX,decimals=3)
Out[45]:
array([[ 9.474, 9.611],
[ 9.611, 16.868]])
In [46]:
# if we calculate the eigenvectors of the covariance matrix, they are the requested operator in PCA
VARs,PCs = np.linalg.eig(XTX)
# VARs,PCs = np.linalg.eig(np.cov(X.T))
indsort = np.argsort(VARs*-1,)
PCs = PCs[:,indsort]
VARs = VARs[indsort]
print np.sum(VARs)
VARs = VARs/np.sum(VARs)*20
26.3420192865
In [47]:
PCs
Out[47]:
array([[-0.56612857, -0.82431695],
[-0.82431695, 0.56612857]])
In [48]:
fig = plt.figure(figsize=(7,7))
ax1= plt.subplot(111)
plt.plot(X[:,0],X[:,1],'.r',markersize=10,alpha=.4 );
plt.plot([0,PCs[0,0]*VARs[0]],[0,PCs[1,0]*VARs[0]],'-og')
plt.plot([0,PCs[0,1]*VARs[1]],[0,PCs[1,1]*VARs[1]],'-ob')
plt.grid();
plt.axis('equal');
In [49]:
PCs
Out[49]:
array([[-0.56612857, -0.82431695],
[-0.82431695, 0.56612857]])
In [50]:
VARs = VARs/np.sum(VARs)
VARs
Out[50]:
array([ 0.89092398, 0.10907602])
In [51]:
fig = plt.figure(figsize=(7,7))
X_trans = X.dot(PCs[:])
plt.plot(X[:,0],X[:,1],'.r',markersize=10,alpha=.4 );
plt.plot(X_trans[:,0],X_trans[:,1],'.b',markersize=10,alpha=.4 );
plt.grid();
plt.axis('equal');
In [52]:
fig = plt.figure(figsize=(7,7))
X_trans = X.dot(PCs[:])
plt.plot(X[:,0],X[:,1],'.r',markersize=10,alpha=.4 );
plt.plot(X_trans[:,0],X_trans[:,1],'.b',markersize=10,alpha=.4 );
# Parametric transformation
X_ = X_trans.dot(([1,1.0]*PCs).T)
plt.plot(X_ [:,0],X_ [:,1],'.g',markersize=10,alpha=.4 );
plt.grid();
plt.axis('equal');
In [53]:
X_trans = X.dot(PCs[:,0])
plt.plot(X_trans,'.r',markersize=10,alpha=.4 );
X_trans = X.dot(PCs[:,1])
plt.plot(X_trans,'.b',markersize=10,alpha=.4 );
In [54]:
# look how independent they are
X_trans = X.dot(PCs)
DF = pd.DataFrame(data=X_trans)
from pandas.tools.plotting import scatter_matrix
scatter_matrix(DF, alpha=0.2, figsize=(6, 6), diagonal='hist');
In [55]:
# This shows the orthogonality
XtrsnTXtrsn = X_trans.T.dot(X_trans)/(X_trans.shape[0]-1)
np.around(XtrsnTXtrsn,decimals=3)
Out[55]:
array([[ 23.469, -0. ],
[ -0. , 2.873]])
A more exciting example¶
In [56]:
from sklearn.datasets import fetch_mldata
from sklearn.datasets import fetch_olivetti_faces
# Face data set
image_shape = (64, 64)
dataset = fetch_olivetti_faces()
faces = dataset.data[range(0,400,10)]
faces = dataset.data[:]
X = faces[:]
X.shape
Out[56]:
(400, 4096)
In [57]:
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(faces[i].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
In [58]:
def PCA(Y):
Y_mean = np.mean(Y,axis=0)
Y = Y - Y_mean
# local centering
# Y -= Y.mean(axis=1).reshape(Y.shape[0], -1)
YTY = Y.T.dot(Y)
VARs,PCs = np.linalg.eig(YTY)
VARs = np.real(VARs)
PCs = np.real(PCs)
indsort = np.argsort(VARs*-1,)
PCs = PCs[:,indsort]
VARs = VARs[indsort]
VARs = VARs/np.sum(VARs)
return PCs,VARs
In [59]:
PCs,VARs = PCA(X)
In [60]:
PCs.shape
Out[60]:
(4096, 4096)
Eigen Pictures¶
In [61]:
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(PCs[:,400+i].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
In [62]:
PCs[0].dot(PCs[11])
Out[62]:
2.1827873e-08
In [63]:
# Explained Variance
plt.plot(np.cumsum(VARs[:10]));
In [64]:
# look how independent they are
X_trans = X.dot(PCs[:,:5])
DF = pd.DataFrame(data=X_trans)
from pandas.tools.plotting import scatter_matrix
scatter_matrix(DF, alpha=0.2, figsize=(6, 6), diagonal='hist');
Using PCA as a generative tool¶
In [126]:
def generate(p0=None,p1=None,p2=None,p3=None,p4=None,p5=None,p6=None,p7=None,p8=None,p9=None):
fig = plt.figure(figsize=(7,7))
x = np.asarray([p0,p1,p2,p3,p4,p5,p6,p7,p8,p9]).T[np.newaxis,:]
n_comps = x.shape[1]
# X_trans = X.dot(PCs[:,:n_comps])
x_ = x.dot(PCs[:,:n_comps].T)
# X_ = x_ + X_mean
plt.subplot(2,1,1)
plt.imshow(x_.reshape(image_shape),cmap=plt.cm.Greys_r);
plt.xticks([]);
plt.yticks([]);
In [127]:
fig = plt.figure(figsize=(7,7))
coeffs = np.random.randn(4,1)
n_comps = coeffs.shape[0]
sel_pcs = PCs[:,:n_comps]
x_ = sel_pcs.dot(coeffs)
columns = []
for i in range(sel_pcs.shape[0]):
columns.append('pc_'+str(i))
columns.append('coeffs')
df = pd.DataFrame(data=np.concatenate((sel_pcs.T,coeffs),axis=1),columns=columns)
plt.subplot(2,1,1)
plt.imshow(x_.reshape(image_shape),cmap=plt.cm.Greys_r);
plt.xticks([]);
plt.yticks([]);
In [128]:
from ipywidgets import interact, HTML, FloatSlider
# interact(generate,a0=(a, b,.2));
interact(generate,p0=(-3,3,.1),p1=(-3,3,.1),p2=(-3,3,.1),p3=(-3,3,.1),p4=(-3,3,.1),
p5=(-3,3,.1),p6=(-3,3,.1),p7=(-3,3,.1),p8=(-3,3,.1),p9=(-3,3,.1));
Chairs¶
In [139]:
from sklearn.datasets import fetch_mldata
from sklearn.datasets import fetch_olivetti_faces
#Chairs
path = "./Data/chairs.csv"
D = pd.read_csv(path,header=None)
image_shape = (64,64)
X = D.values[:]
print X.shape
# # Mnist data set
# image_shape = (28, 28)
# dataset = fetch_mldata('MNIST original')
# # faces = dataset.data
# X = faces[:]
# X.shape
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(X[i].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
(696, 4096)
In [140]:
PCs,VARs = PCA(X)
In [141]:
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(PCs[:,i].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
In [142]:
# Explained Variance
plt.plot(np.cumsum(VARs[:100]));
In [143]:
from ipywidgets import interact, HTML, FloatSlider
# interact(generate,a0=(a, b,.2));
interact(generate,p0=(-3,3,.1),p1=(-3,3,.1),p2=(-3,3,.1),p3=(-3,3,.1),p4=(-3,3,.1),
p5=(-3,3,.1),p6=(-3,3,.1),p7=(-3,3,.1),p8=(-3,3,.1),p9=(-3,3,.1));
Floor PLans¶
In [144]:
from sklearn.datasets import fetch_mldata
from sklearn.datasets import fetch_olivetti_faces
# floorplan
path = "./Data/1000FloorPlans.csv"
D = pd.read_csv(path,header=None)
image_shape = (50, 50)
faces = D.values[:]
faces[faces>0] = -1
faces[faces==0] = 1
faces[faces==-1] = 0
X = faces[:]
X.shape
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(X[i].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
In [145]:
PCs,VARs = PCA(X)
In [146]:
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(PCs[:,i].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
In [147]:
from ipywidgets import interact, HTML, FloatSlider
# interact(generate,a0=(a, b,.2));
interact(generate,p0=(-3,3,.1),p1=(-3,3,.1),p2=(-3,3,.1),p3=(-3,3,.1),p4=(-3,3,.1),
p5=(-3,3,.1),p6=(-3,3,.1),p7=(-3,3,.1),p8=(-3,3,.1),p9=(-3,3,.1));
Extensions to PCA¶
- Independent CA (ICA)
- Where we relax the assumption of orthogonality of compenents
- Kernel PCA
- Will be discussed with Support Vector Machines and Kernel Tricks
- LDA
- LSA
- Factor Analysis
- Ranom Projection
- Randomized pca
- ** Stack of PCAs**
- Toward Deep networks of Autoencoders
Go here with all the extensions:¶
http://scikit-learn.org/stable/modules/classes.html#module-sklearn.decomposition
In [148]:
# floorplan
path = "./Data/1000FloorPlans.csv"
D = pd.read_csv(path,header=None)
image_shape = (50, 50)
faces = D.values[:]
faces[faces>0] = -1
faces[faces==0] = 1
faces[faces==-1] = 0
X = faces[:]
X.shape
Out[148]:
(999, 2500)
In [149]:
from sklearn.decomposition import sparse_encode
K = 200
from sklearn.decomposition import MiniBatchDictionaryLearning
sc = MiniBatchDictionaryLearning(K)
sc.fit(X)
Out[149]:
MiniBatchDictionaryLearning(alpha=1, batch_size=3, dict_init=None,
fit_algorithm='lars', n_components=200, n_iter=1000,
n_jobs=1, random_state=None, shuffle=True, split_sign=False,
transform_algorithm='omp', transform_alpha=None,
transform_n_nonzero_coefs=None, verbose=False)
In [150]:
sc.components_.shape
Out[150]:
(200, 2500)
In [151]:
fig = plt.figure(figsize=(10,20))
for i in range(200):
plt.subplot(20,10,i+1)
plt.imshow(sc.components_[i,:].reshape(image_shape),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout(h_pad=.01, w_pad=.01)
In [57]:
code = sparse_encode(X, sc.components_)
In [ ]:
In [152]:
X.shape
Out[152]:
(999, 2500)
In [153]:
code.shape
Out[153]:
(999, 200)
In [154]:
i = 100
reconstructed_pic = code[i].dot(sc.components_)
In [155]:
plt.subplot(2,1,1)
plt.imshow(X[i].reshape(image_shape),cmap=plt.cm.gray);
plt.subplot(2,1,2)
plt.imshow(reconstructed_pic.reshape(image_shape),cmap=plt.cm.gray);
In [156]:
plt.plot(code[i])
Out[156]:
[<matplotlib.lines.Line2D at 0x11da0a610>]
Now to generate new things?¶
In [157]:
# if we use any random weight?
randcod = np.random.randint(-6,high=10,size=200)[np.newaxis,:]
reconstructed_pic = randcod.dot(sc.components_)
plt.imshow(reconstructed_pic.reshape(image_shape),cmap=plt.cm.gray);
In [158]:
# But if we learn the space of codes (a 200 dimensional space in this example)
# in Principle, similar floor plans have similar codes
for i in range(10):
plt.plot(code[i]);
In [159]:
from sklearn.feature_extraction.image import extract_patches_2d
rng = np.random.RandomState(0)
patch_size = (20, 20)
buffer = []
for img in X:
data = extract_patches_2d(img.reshape(image_shape), patch_size, max_patches=100,
random_state=rng)
data = np.reshape(data, (len(data), -1))
buffer.extend(data)
Patch_X = np.asarray(buffer)
In [160]:
len(Patch_X)
Out[160]:
99900
In [161]:
fig = plt.figure(figsize=(12,12))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(Patch_X[1000+i].reshape(patch_size),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout()
In [162]:
from sklearn.decomposition import sparse_encode
K = 200
from sklearn.decomposition import MiniBatchDictionaryLearning
# MiniBatchDictionaryLearning(n_components=200, alpha=1, n_iter=500)
sc_patch = MiniBatchDictionaryLearning(n_components=K,n_iter=2000)
sc_patch.fit(Patch_X)
Out[162]:
MiniBatchDictionaryLearning(alpha=1, batch_size=3, dict_init=None,
fit_algorithm='lars', n_components=200, n_iter=2000,
n_jobs=1, random_state=None, shuffle=True, split_sign=False,
transform_algorithm='omp', transform_alpha=None,
transform_n_nonzero_coefs=None, verbose=False)
In [163]:
fig = plt.figure(figsize=(10,20))
for i in range(200):
plt.subplot(20,10,i+1)
plt.imshow(sc_patch.components_[i,:].reshape(patch_size),cmap=plt.cm.gray);
plt.xticks([]);
plt.yticks([]);
plt.tight_layout(h_pad=.01, w_pad=.01)
In [164]:
code_patch = sparse_encode(Patch_X[:1000], sc_patch.components_)
In [165]:
i = 100
reconstructed_patch = code_patch[i].dot(sc_patch.components_)
In [166]:
plt.subplot(2,1,1)
plt.imshow(Patch_X[i].reshape(patch_size),cmap=plt.cm.gray);
plt.subplot(2,1,2)
plt.imshow(reconstructed_patch.reshape(patch_size),cmap=plt.cm.gray);
In [167]:
# But if we learn the space of codes (a 200 dimensional space in this example)
# in Principle, similar floor plans have similar codes
for i in range(10):
plt.plot(code_patch[i]);