Data Driven Modeling¶
### PhD seminar series at Chair for Computer Aided Architectural Design (CAAD), ETH Zurich

Topics to be discussed¶
Probability Theory
- Certainty and Determinism
- Laplace’s demon
- Poncare and the end of determinism
- Deterministic Unpredictability (Chaos Theory and Bifurcation)
- Uncertainty and Randomness
- Fuzziness, vagueness and ambiguity
- Variable and Parameter
- Random Variable
- Probability (Kolmogrov) axioms
- Independent Random Variables
- Joint Probability
- Baysian Rules and Conditional Probability
- Probability distributions
- Expected Value
- Variance
- Covariance
- Law of Large Numbers
- Central Limit Theorem
In [1]:
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
pd.__version__
import sys
import sompylib.sompy as SOM
import sompylib1.sompy as SOM1
%matplotlib inline
In [2]:
from IPython.display import YouTubeVideo
YouTubeVideo('EZNpnCd4ZBo',width=700, height=600)
Out[2]:
In [1]:
# Double pendulum formula translated from the C code at
# http://www.physics.usyd.edu.au/~wheat/dpend_html/solve_dpend.c
from numpy import sin, cos
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
import matplotlib.animation as animation
G = 9.8 # acceleration due to gravity, in m/s^2
L1 = 1.0 # length of pendulum 1 in m
L2 = 0.7 # length of pendulum 2 in m
M1 = 1.0 # mass of pendulum 1 in kg
M2 = 1.0 # mass of pendulum 2 in kg
def derivs(state, t):
dydx = np.zeros_like(state)
dydx[0] = state[1]
del_ = state[2] - state[0]
den1 = (M1 + M2)*L1 - M2*L1*cos(del_)*cos(del_)
dydx[1] = (M2*L1*state[1]*state[1]*sin(del_)*cos(del_) +
M2*G*sin(state[2])*cos(del_) +
M2*L2*state[3]*state[3]*sin(del_) -
(M1 + M2)*G*sin(state[0]))/den1
dydx[2] = state[3]
den2 = (L2/L1)*den1
dydx[3] = (-M2*L2*state[3]*state[3]*sin(del_)*cos(del_) +
(M1 + M2)*G*sin(state[0])*cos(del_) -
(M1 + M2)*L1*state[1]*state[1]*sin(del_) -
(M1 + M2)*G*sin(state[2]))/den2
return dydx
# create a time array from 0..100 sampled at 0.05 second steps
dt = 0.05
t = np.arange(0.0, 30, dt)
# th1 and th2 are the initial angles (degrees)
# w10 and w20 are the initial angular velocities (degrees per second)
th1 = 120.0
w1 = 0.0
th2 = -10.0
w2 = 0.0
# initial state
state = np.radians([th1, w1, th2, w2])
# integrate your ODE using scipy.integrate.
y = integrate.odeint(derivs, state, t)
x1 = L1*sin(y[:, 0])
y1 = -L1*cos(y[:, 0])
x2 = L2*sin(y[:, 2]) + x1
y2 = -L2*cos(y[:, 2]) + y1
fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-2, 2), ylim=(-2, 2))
ax.grid()
line, = ax.plot([], [], 'o-r',markersize=3, lw=2)
trace1, = ax.plot([], [], '-', c='r',lw=.4)
trace2, = ax.plot([], [], '-', c='g',lw=.4)
time_template = 'time = %.1fs'
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
def init():
line.set_data([], [])
trace1.set_data([], [])
trace2.set_data([], [])
time_text.set_text('')
return line, time_text
def animate(i):
thisx = [0, x1[i], x2[i]]
thisy = [0, y1[i], y2[i]]
line.set_data(thisx, thisy)
trace1.set_data(x1[:i], y1[:i])
trace2.set_data(x2[:i], y2[:i])
time_text.set_text(time_template % (i*dt))
return line, time_text
ani = animation.FuncAnimation(fig, animate, np.arange(1, len(y)),
interval=25, blit=True, init_func=init)
# ani.save('./Images/double_pendulum.mp4', fps=15)
ani.save('./Images/double_pendulum.mp4', fps=15, extra_args=['-vcodec', 'libx264'],dpi=200)
plt.close()
In [2]:
from IPython.display import HTML
HTML("""
<video width="600" height="400" controls>
<source src="files/Images/double_pendulum.mp4" type="video/mp4">
</video>
""")
Out[2]:
In [4]:
from IPython.display import YouTubeVideo
YouTubeVideo('04mbMblhXog',width=600, height=400)
Out[4]:
In [5]:
plt.plot(range(len(x2)),x2);
In [6]:
xa=.15
xb=3.
C=np.linspace(xa,xb,num=100)
# print C
iter=range(1000)
Y = C*0+1
YS = []
for x in iter:
Y=Y**2-C
# plt.plot(C,Y, '.k', markersize = 2)
for x in iter:
Y = Y**2 - C
YS.append(Y)
plt.plot(C,Y, '.k', markersize = 2);
plt.xlabel('C')
plt.ylabel('Y')
plt.show();
In [7]:
YS = np.asarray(YS)
#Change this parameter and see how the range of possible values is changing
which_c = 50
plt.plot(YS[:,which_c][:200],'.-');
print 'C : {}'.format(C[which_c])
plt.xlabel('Iterations')
plt.ylabel('Y')
C : 1.58939393939
Out[7]:
<matplotlib.text.Text at 0x11ef54dd0>
Simulation of Lorenz Attractors¶
In [8]:
#Code from: https://jakevdp.github.io/blog/2013/02/16/animating-the-lorentz-system-in-3d/
# import numpy as np
# from scipy import integrate
# # Note: t0 is required for the odeint function, though it's not used here.
# def lorentz_deriv((x, y, z), t0, sigma=10., beta=8./3, rho=28.0):
# """Compute the time-derivative of a Lorenz system."""
# return [sigma * (y - x), x * (rho - z) - y, x * y - beta * z]
# x0 = [1, 1, 1] # starting vector
# t = np.linspace(0, 3, 1000) # one thousand time steps
# x_t = integrate.odeint(lorentz_deriv, x0, t)
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import cnames
from matplotlib import animation
%matplotlib inline
N_trajectories = 30
#dx/dt = sigma(y-x)
#dy/dt = x(rho-z)-y
#dz/dt = xy-beta*z
def lorentz_deriv((x, y, z), t0, sigma=10., beta=8./3, rho=28.0):
"""Compute the time-derivative of a Lorentz system."""
return [sigma * (y - x), x * (rho - z) - y, x * y - beta * z]
# Choose random starting points, uniformly distributed from -15 to 15
np.random.seed(1)
x0 = -15 + 30 * np.random.random((N_trajectories, 3))
# Solve for the trajectories
t = np.linspace(0, 10, 1000)
x_t = np.asarray([integrate.odeint(lorentz_deriv, x0i, t)
for x0i in x0])
# Set up figure & 3D axis for animation
fig = plt.figure()
ax = fig.add_axes([0, 0, 1, 1], projection='3d')
ax.axis('off')
plt.set_cmap(plt.cm.YlOrRd_r)
# choose a different color for each trajectory
colors = plt.cm.jet(np.linspace(0, 1, N_trajectories))
# set up lines and points
lines = sum([ax.plot([], [], [], '-', c=c)
for c in colors], [])
pts = sum([ax.plot([], [], [], 'o', c=c)
for c in colors], [])
# prepare the axes limits
ax.set_xlim((-25, 25))
ax.set_ylim((-35, 35))
ax.set_zlim((5, 55))
# set point-of-view: specified by (altitude degrees, azimuth degrees)
ax.view_init(30, 0)
# initialization function: plot the background of each frame
def init():
for line, pt in zip(lines, pts):
line.set_data([], [])
line.set_3d_properties([])
pt.set_data([], [])
pt.set_3d_properties([])
return lines + pts
# animation function. This will be called sequentially with the frame number
def animate(i):
# we'll step two time-steps per frame. This leads to nice results.
i = (2 * i) % x_t.shape[1]
for line, pt, xi in zip(lines, pts, x_t):
x, y, z = xi[:i].T
line.set_data(x, y)
line.set_3d_properties(z)
pt.set_data(x[-1:], y[-1:])
pt.set_3d_properties(z[-1:])
ax.view_init(30, 0.3 * i)
fig.canvas.draw()
return lines + pts
# instantiate the animator.
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=500, interval=10, blit=True)
# Save as mp4. This requires mplayer or ffmpeg to be installed
anim.save('./Images/lorentz_attractor.mp4', fps=15, extra_args=['-vcodec', 'libx264'],dpi=200)
plt.close()
In [9]:
from IPython.display import HTML
HTML("""
<video width="600" height="400" controls>
<source src="files/Images/lorentz_attractor.mp4" type="video/mp4">
</video>
""")
Out[9]:
In [5]:
from IPython.display import YouTubeVideo
YouTubeVideo('JZoGO0MrZPA',width=400, height=400)
Out[5]:
In [10]:
# No regularity in the behavior
# The effect of initial value
figure =plt.figure(figsize=(10,10))
for i in range(20):
plt.subplot(5,4,i+1);
plt.plot(x_t[i,:,1]);
plt.xlabel('time')
plt.ylabel('x')
plt.tight_layout();
Non-Predictable Determinism --- > End of Determinism?!¶
- Dependency to initial conditions and parameters
- Butterfly Effect
- Henri Poncare's work on N-Body Problem 1880s
- Lorenz Attractors 1960s
- Further readings:
- Deterministic Nonperiodic Flow: #Paper: http://eaps4.mit.edu/research/Lorenz/Deterministic_63.pdf
- Heisenberg's uncertainty principle
- "God Doesn't play dice"
- Is randomness the nature of things or due to lack of understanding?
- Is it appropriate to look at probability and statistics as some sorts of pragmatism?
- Important people from the History of Probability and Statistics: http://www.economics.soton.ac.uk/staff/aldrich/Figures.htm
Important terms¶
Variable¶
- a symbolization of specific number, vector, matrix or even a function, which takes a range of values
- Then, we have discrete or continuous variables, depending on the range of values
- Dependent and independent variables $$y = 2x + sin(x) $$
Parameter or Constant¶
- A Variable, which we assume is not varying (i.e. is constant) in our experiment
Random Variable (contribution of probability theory)¶
- To add likelihood or chance (or formally probability) to any values of a variable
Fuzziness, vagueness and ambiguity (possibility theory)¶
¶
¶
Some important principles of Probability Theory¶
Probability (Kolmogrov) axioms¶
https://en.wikipedia.org/wiki/Probability_axioms
* **First axiom**
* **Second axiom**
* sum of all probabilities
* Third axiom
* probability of disjoint elements is the sum of their individual probabilities
* **Consequences**
¶
¶
¶
- Some set theoretical intuitions
- venn diagrams from set theory
¶

- Conditional Probability
¶

¶
- Independent variables
- results of coin toss and rolling a dice
¶
¶
- Law of total probability

¶
- Bayes Rule
¶

Further readings¶
- A First Course on Probability by Sheldon Ross
- Richard Feynman intro to probability theory: http://www.feynmanlectures.caltech.edu/I_06.html
¶
Random Variable¶
A random variable is always coming with a likelihood function (probability density)¶
discrete random variable¶
- examples: Coin:{'head','tail'},
- Dice:{1,...,6}
- Probability mass function indicates the likelihood of each discrete event
continuous random variable¶
- temperature in a building
- Height of a random person
- Probability Density function indicates the likelihood of each discrete event
- Cumulative distribution function
- joint functions
¶
- Expected value
¶
- Variance
¶
- CoVariance
¶
Therefore, two independent (uncorelated) variables have a covariance of zero and not the other way necessarily¶
Covariance is the heart of many ML and statistical learning methods such as PCA.¶
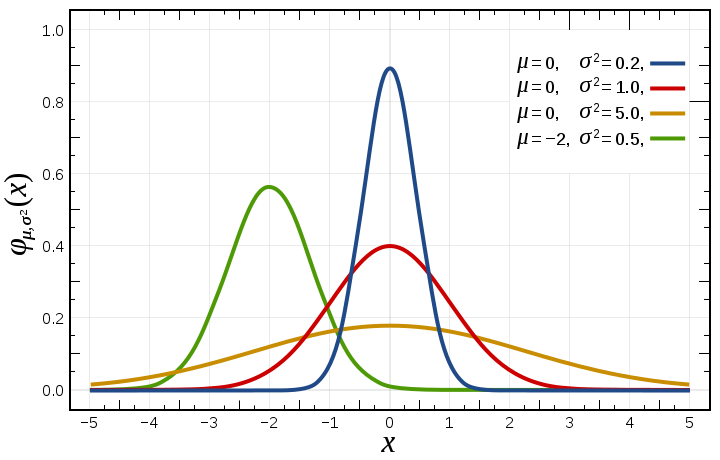
Known probability functions¶
- There are many more : https://en.wikipedia.org/wiki/List_of_probability_distributions
Nevertheless, we use computers!¶
In [6]:
from scipy.integrate import quad
#Now CDF
#P(a<=x<=b) for N(m,s)
# Gaussian Distribution
def Guassianf(m,s,x):
return 1/(s*np.sqrt(2*np.pi)) * np.exp(-np.power((x-m),2)/(2*s*s))
def integrand(x,m,s,Guassianf):
return Guassianf(m,s,x)
a = -6
b= 6
m = 0
s = 1
P, err = quad(integrand, a, b,args=(m,s,Guassianf))
print P
0.999999998027
In [12]:
#Expected Value and Variance
from scipy.integrate import quad
def integrand(x,m,s,Guassianf):
return x*Guassianf(m,s,x)
a = -1*np.inf
b= np.inf
m = 2
s = 10
mu, err = quad(integrand, a, b,args=(m,s,Guassianf))
def integrand(x,m,s,Guassianf):
return x*x*Guassianf(m,s,x)
mu2, err = quad(integrand, a, b,args=(m,s,Guassianf))
sigma2 = mu2- mu*mu
print mu,sigma2
2.0 100.0
In [13]:
from scipy.integrate import quad
# Uniform Distribution
def f(a,b):
return 1/float(b-a)
def integrand(x,a,b,f):
return x*f(a,b)
a = 0
b= 10
mu, err = quad(integrand, a, b,args=(a,b,f))
def integrand(x,a,b,f):
return x*x*f(a,b)
mu2, err = quad(integrand, a, b,args=(a,b,f))
sigma2 = mu2- mu*mu
print mu,sigma2
5.0 8.33333333333
But before going further¶
- we talked about end of determinism, and transition from knowing to learning but
- It seems that there is again some sort of repetition of learning and knowing withing probability and statistics
In [14]:
import datetime
import pandas as pd
import pandas.io.data
import numpy as np
from matplotlib import pyplot as plt
import sys
import getngrams as ng# from pandas import Series, DataFrame
# import xkcd as fun
%matplotlib inline
# kw = ['Mainframe Computer','Personal Computer','Sensor','Computer Network','Internet', 'Data Mining','Pervasive Computing',
# 'Smart Phone','Communication Technology','Simulation','Micro Simulation','Web 2.0'
# ]
kw = ['Probability','Statistics','Machine Learning','stochastics']
A = pd.DataFrame()
for i in range(len(kw)):
try:
tmp = ng.runQuery('-nosave -noprint -startYear=1800 -smoothing=3 -endYear=2008 -caseInsensitive '+kw[i])
# A['year']=tmp.year.values[:]
weights = tmp.values[:,1:]
mx = np.max(weights,axis=0)
mn = np.min(weights,axis=0)
R = mx-mn
weights = (weights-mn)/R
tmp.ix[:,1:]=weights
A[kw[i]]=tmp.values[:,1]
except:
print kw[i], 'not enough data'
In [15]:
fig = plt.figure()
for i in range(len(kw)):
try:
plt.plot(tmp.year,A[kw[i]],linewidth=1,label=kw[i])
xticks = np.arange(tmp.year[0],2011,10).astype(int)
plt.xticks(xticks)
# plt.yticks([])
except:
print kw[i], 'not enough data'
# A.plot(A.year,A.columns[1:],label='Date',colormap='jet')
#
plt.legend(loc='best',bbox_to_anchor = (1.0, 1.0),fontsize = 'medium')
fig.set_size_inches(14,7)
Seems now it makes sense to use the term of Learning in Machine Learning!¶
Further readings¶
- Statistical Modeling: The Two Cultures by Leo Breiman http://www.stat.uchicago.edu/~lekheng/courses/191f09/breiman.pdf
- all the fights between statisticians and ML guys!
Next sessions we talk about these estimation methods in details...¶
The answer to the excersice¶
In [2]:
from scipy.integrate import quad
# Exponential
def f(m,x):
return lam*np.exp(-1*lam*x)
def integrand(x,lam,f):
return x*f(lam,x)
a = 0
b= np.inf
lam = 2
mu, err = quad(integrand, a, b,args=(lam,f))
def integrand(x,lam,f):
return x*x*f(lam,x)
mu2, err = quad(integrand, a, b,args=(lam,f))
sigma2 = mu2- mu*mu
print mu,sigma2