সাইকিট-লার্ন এর ডাটা লে-আউট, ডাটা হ্যান্ডলিং¶
রিভিশন ৫
কম্পিউটারের ডাটা রাখার ধারণা¶
(না পড়লেও চলবে)
আমরা তো এটা বুঝে গেছি যে মেশিন লার্নিং মডেল তৈরি করে ডাটা থেকে। ভালো কথা। তো, ডাটা এক্সেস করবো কিভাবে? আর, তাই কম্পিউটার কিভাবে ডাটা রাখে সেটা নিয়ে কিছুটা আলাপ করা যায় বরং। তবে, সেটার স্কোপ কমিয়ে আনার জন্য আমার প্রস্তাব হচ্ছে, "সাইকিট-লার্ন" কিভাবে ডাটা রাখে সেটা বোঝা দরকার। রেডি তো?
আমার ‘মেশিন লার্নিং’ এর হাতে খড়ি হয় ‘আর’ প্রোগ্রামিং এনভারমেন্ট দিয়ে। একটা অসাধারণ এনভায়রনমেন্ট বটে। আপনারা সবাই জানেন যে ‘আর’ এর কাজ শুরু হয় পরিসংখ্যান এর ধারণা থেকে। আজকে ‘মেশিন লার্নিং’ এর যত ধারণা তার বেশিরভাগ মানে প্রায় সবকিছুই এসেছে এই পরিসংখ্যান থেকে। বলতে পারেন কম্পিউটারের ‘প্রসেসিং পাওয়ার’ এবং 'ডাটা স্টোরেজে'র দাম কমাতে অনেক ডাটা অল্প খরচে প্রসেসিং করার সুবিধা পেল মানুষ। সেই সাথে বুঝতে শুরু করেছে ডাটা কিভাবে আমাদের জীবনকে পাল্টাচ্ছে।
কম্পিউটার ডাটা রাখে নিচের ছবির মতো করে। মানে একেবারে ইউনিট লেভেলে। মনে আছে ভেক্টর, ম্যাট্রিক্স, অ্যারে, ডাটাফ্রেম, পাইথনের লিস্ট এর কথা? এরাই ডাটা রাখে --- কখনো বিভিন্ন সারি আর কলাম নিয়ে। আবার কয়েক ডাইমেনশন নিয়ে। আচ্ছা, এক ধরণের জিনিস তো এক জায়গায় রাখা যায় তবে কি হতে পারে যখন বিভিন্ন জিনিস রাখবো এক টেবিলে?
সারি ধরে ডাটা রাখার সবচেয়ে ছোট ইউনিট ধরতে পারি এখানে ভেক্টরকে। একটা ভেক্টর হচ্ছে এক ডাইমেনশনের একটা কালেকশন - যেটা হতে পারে লিস্ট, সেট, নামপাই অ্যারে (numpy.array) অথবা পান্ডাজ সিরিজ (pandas.series) - নিচের ছবি দেখুন। আবার, নামপাই এর একটা অ্যারে কয়েক ডাইমেনশনের হতে পারে। একারণে একে আমরা বলি 'এনডি' অ্যারে। মানে “এন” সংখ্যক অ্যারে। এই কনটেইনারে একই টাইপ আর সাইজের জিনিস থাকবে। আর ম্যাট্রিক্স হচ্ছে দুই ডাইমেনশনের একটা কনটেইনার, যেখানে সারি, কলাম সহ একটা নেস্টেড লিস্ট বা নামপাই অ্যারে (numpy.array) অথবা পান্ডাজ ডাটাফ্রেম (pandas.DataFrame) থাকতে পারে।
তবে ডাটা সায়েন্টিস্টরা ভালোবাসেন ডাটাফ্রেম। সত্যি বলতে - বিভিন্ন ধরনের ডাটাকে এক জায়গায় রাখার জন্য চমৎকার জিনিস হচ্ছে ‘ডাটাফ্রেম’। মনে আছে এক্সেল এর কথা? এক্সেলের টেবিলটাকে আমরা “আর প্রোগ্রামিং” এনভারমেন্টে “ডাটাফ্রেম” বলি। আর এই ডাটাফ্রেম নিয়ে কাজ করতে করতে এর সুবিধা চলে এসেছে বাকি সব প্লাটফর্মে। ডাটাফ্রেম হচ্ছে দুই ডাইমেনশনের বিভিন্ন রকম জিনিসপত্র রাখার অ্যারে। আগেই বলেছি জিনিসটা দেখতে একেবারে আমাদের এক্সেলশিটের মতো। এই ডাটাফ্রেম নিয়ে কাজ করার জন্য পাইথনে আমরা ব্যবহার করি ‘পান্ডাজ’। ডাটাফ্রেমে আমাদের দরকারি ডাটা স্ট্রাকচারে ডাটা ‘ম্যানুপুলেশন’ খুবই সোজা। সত্যি বলতে ‘আর’ প্রোগ্রামিং এনভারমেন্ট এর সব সুবিধা নিয়ে এসেছে এই পান্ডাজ। আমাদের ডাটাফ্রেমে তিনটা আসল কম্পোনেন্ট থাকে। ১. ডাটা ২. ইনডেক্স ৩. কিছু কলাম। একটা ডাটাফ্রেমে, ডাটা হিসেবে নিচের কয়েকটা জিনিস থাকে।
শুরুতেই পাণ্ডাজের ডাটাফ্রেম। সেটা তো অবশ্যই।
পাণ্ডাজের সিরিজ। এটা একটা এক ডাইমেনশনের লেবেলসহ অ্যারে, সঙ্গে থাকছে অ্যাক্সিস এর লেবেল বা ইন্ডেক্স। সোজা কথায়, একটা সিরিজ অবজেক্ট হচ্ছে ডাটাফ্রেমের একটা কলাম। বোঝা গেছে তো?
'নামপাই' 'এনডি' অ্যারে। আমরা এটাকে রেকর্ড বলতে পারি।
দুই ডাইমেনশনের অ্যারে। আগেই বলেছি - ‘এনডি’ অ্যারে হচ্ছে ‘এন’ সংখ্যক অ্যারে।
ডিকশনারি অথবা এক ডাইমেনশনের ‘এনডি’ অ্যারে, লিস্ট অথবা ডিকশনারি অথবা সিরিজ।
আমরা এখানে একটা ছবি দেই বরং।
এখানে একটা "নামপাই অ্যারে" তৈরি করলাম। আবার সেই "অ্যারে"কে ঢুকিয়ে দিলাম ডাটাফ্রেমে।
import numpy as np # ইমপোর্ট করার ব্যাপারটা একটু পরে বুঝবো
data = np.array([['','Col1','Col2'],
['Row1',1,2],
['Row2',3,4]])
data
import pandas as pd # এই ব্যাপারটা পরে বুঝবো
print(pd.DataFrame(data=data[1:,1:],
index=data[1:,0],
columns=data[0,1:]))
সাইকিট-লার্ন এর ডাটা নিয়ে কাজ করার ধারণা¶
(এখান থেকে পড়তেই হবে)
সাইকিট-লার্ন এর নিজস্ব ডাটা হ্যান্ডলিং এবং এর ভেতরের ডাটা রিপ্রেজেনটেশন অসম্ভব ভালো। কাজ করে বুঝেছি। পাইথনের লিস্ট, নামপাই অ্যারে, স্কিপি ম্যাট্রিক্স, পান্ডাজের ডাটাফ্রেম তার জন্য কোন সমস্যা নয়। যেহেতু মডেল ট্রেনিং এর জন্য আলাদা করে ডাটাফ্রেমের দরকার পড়ছে না সেকারণে শুরুতে লিস্ট, নামপাই অ্যারে দিয়ে শুরু করা যায়। আর সেটাই করেছে সাইকিট-লার্ন। "স্টার্ট স্মল"। "নামপাই অ্যারে" দিয়ে শুরু এর ভেতরের ডাটাসেটগুলো। আমাদের এখানে যেহেতু দুই ডাইমেনশনাল অ্যারে নিয়ে কাজ করবো, সেজন্য "নামপাই অ্যারে" আর "ম্যাট্রিক্স" কথাটা ইন্টারচেন্জেবল। মনে থাকবে তো?
আমরা যতো সামনে এগুবো ততো আমাদের বিভিন্ন ভ্যারিয়েবলের ব্যবহার বাড়বে। সেখানে একটা কনভেনশন ব্যবহার করলে পৃথিবীর বাকি ডাটা সায়েন্টিস্টদের সাথে আমরা একভাবে এগুতে পারবো। আমাকে প্রচুর 'স্ট্যাকওভারফ্লো'তে সময় দিতে হয় বলে -সেখানে মেশিন লার্নিং এর পৃথিবীর বেস্ট প্রাকটিসগুলোকে সামনে নিয়ে আসবো। আমার দেখামতে X, y, n, df, np, data, dataframe, train, test, results, final_results, predict, fit ইত্যাদি ইত্যাদি ভ্যারিয়েবল আসবে সামনে। এগুলোর ব্যবহার আমরা দেখাবো নির্দিষ্ট ক্ষেত্রগুলোতে।
আমরা যতগুলো ডাটাসেট ব্যবহার করব তার প্রায় সবগুলোই দেয়া আছে সাইকিট-লার্ন এ। ভালো করে দেখলে দেখা যায় যে সবগুলো আছে আলাদা করে একটা ডাটাসেট (datasets.load_iris-আমাদের আইরিস ডাটাসেটের ক্ষেত্রে) মডিউলে। ওই ডাটাগুলোকে নিমিষেই লোড করা যায় এর সাথে দেয়া একেকটা ফাংশন [আমাদের ক্ষেত্রে (load_iris())] দিয়ে।
ডাটা ইমপোর্ট: আইরিস ডাটাসেট¶
শুরুতে sklearn থেকে ডাটাসেটগুলো ইমপোর্ট করছি। অথবা আমরা সরাসরি load_iris ফাংশন ইমপোর্ট করতে পারতাম। দুটো উদাহরণ দিয়েছি এখানে।
# এখানে আমরা সাইকিট লার্ন datasets মডিউল থেকে load_iris ফাংশন ডাকবো
from sklearn import datasets
# from sklearn.datasets import load_iris
অন্যান্য লাইব্রেরি ইমপোর্ট¶
"পান্ডাজ" আর "নামপাই" ছাড়া আমাদের চলবে না। এখন শুরুতে পান্ডাজ না হলেও চলবে। আমরা এখন শুধুমাত্র নামপাই 'অ্যারে' নিয়েই সব কাজ করবো। একটা কথা আমরা মনে রাখবো। "লেস ইজ মোর"। আগেই বলেছি, এখানে 'অ্যারে' আর ম্যাট্রিক্স জিনিসটা একই।
# import pandas as pd
import numpy as np
ডাটা লোড, কী আছে ভেতরে?¶
কাজের শুরুতে ডাটা লোড করে নেই। 'সাইকিট-লার্ন' সেদিক থেকে কাজটাকে আরো সহজ করে দিয়েছে। বাইরে থেকে নতুন করে ডাটা নেয়ার ঝামেলা থাকছেনা। একটা ফাংশন কল করলেই আইরিসের ডাটা চলে আসবে। সবচেয়ে মজার ব্যাপার হলো ডাটাকে আলাদা করে "ফিচার ডাটা" আর "টার্গেট ডাটা" করার ঝামেলা নিতে হবে না আমাদের। এটা একটা বড় সুবিধা। আমরা জানি - মেশিন লার্নিং কনভেশন অনুযায়ী দুটো ডাটা প্রয়োজন আমাদের। ফিচার ডাটা আর টার্গেট ডাটা। কনভেনশন অনুযায়ী তাদের নাম হচ্ছে "ফিচারগুলোর ম্যাট্রিক্স" এবং "টার্গেট অ্যারে"। দুটোই অ্যারে।
# আমরা "bunch" অবজেক্টকে লোড করে নিচ্ছি -> এখানে ডাটাসেট আর তার এট্রিবিউট থাকছে
iris = datasets.load_iris()
# iris = load_iris()
আমরা load_iris() ফাংশন দিয়ে iris নাম দিয়ে যেই অবজেক্টকে ফিরে পাবো সেটা আসলে সাইকিট-লার্ন এর একটা "বাঞ্চ" অবজেক্ট। জিনিসটা আসলে একটা ডিকশনারির মতো। ভেতরে কয়েকটা এলিমেন্ট আছে। কী, ইনডেক্স সহ। ভালো দিক হচ্ছে, সেটা তার বিভিন্ন এট্রিবিউটকে এক্সেস করতে পান্ডাজের মতো ডট নোটেশন (.) সাপোর্ট করে। কী-গুলোতে কোন স্পেস ব্যবহার করা যাবে না। দেখুন, ভেতরে iris.keys(), মানে এর ডাটা বা টার্গেটকে এক্সেস করতে গেলে iris.data বা iris.target ধরে ডাকতে হবে।
# এটা কিন্তু ডাটাফ্রেম নয়, বাঞ্চ অবজেক্ট, ডিকশনারি গোত্রের
# type(iris)
type(datasets.load_iris())
এতো আলাপ করলাম, এখন বলুনতো আমাদের ডাটা টাইপ কী? নামপি এনডি অ্যারে।
print("Type of data:", type(iris['data']))
কিছু মেশিন লার্নিং টার্মিনোলজি¶
প্রতিটা সারি হচ্ছে একটা অবজারভেশন (যাকে আমরা বলি স্যাম্পল, ইনস্ট্যান্স, রেকর্ড, উদাহরণ ইত্যাদি)
প্রতিটা কলাম হচ্ছে একটা ফিচার (যার অন্যান্য নাম হচ্ছে প্রেডিক্টর, অ্যাট্রিবিউট, ইনডিপেনডেন্ট ভ্যারিয়েবল, ইনপুট, রিগ্রেসর, কোভ্যারিয়েট)
প্রতিটা ভ্যালু আমরা যাকে প্রেডিক্ট করবো, সেটার নাম হচ্ছে টার্গেট/রেসপন্স (এর অন্য অনেক নামের মধ্যে আউটকাম, লেবেল, ডিপেনডেন্ট ভ্যারিয়েবল ..)
আমাদের এই সুপারভাইজ্ড লার্নিং এর আউটকাম যেহেতু "ক্লাসিফিকেশন" এর মানে হচ্ছে আমাদের "রেসপন্স" হচ্ছে "ক্যাটেগরিক্যাল"।
যদি আমাদের এই সুপারভাইজ্ড লার্নিং এর রেসপন্স কন্টিনিউয়াস সংখ্যা হতো, সেটাকে আমরা বলতাম "রিগ্রেসন"। সামনে কথা হবে এটা নিয়ে।
এই অবজেক্টের ভেতরে কী আছে?¶
আমরা দেখতে চাইবো আমাদের এই iris অবজেক্টের ভেতরে কি আছে? যেহেতু এটা একটা ডিকশনারি অবজেক্টের মতো, তার একটা ইনডেক্স আছে keys() দিয়ে এক্সেস করার জন্য। এখানে সবচেয়ে বেশি প্রয়োজনীয় জিনিস হচ্ছে 'data' আর 'target' যাকে এক্সেস করবো iris.data এবং iris.target নামে। কাজের শুরু অল্প দিয়ে। ঠিক ধরেছেন। এগুলো ডাটাফ্রেম নয়, বরং দুটোই অ্যারে।
print(iris.keys())
dir(iris) # এটা একটা বিল্ট-ইন পাইথন ফাংশন, প্রায় একই কাজ করে
শুরু করি গল্প পড়ে। আইরিস ডাটাসেট একনজরে। আইরিস ডাটাসেট নিয়ে একটা ডেসক্রিপশন ('DESCR') দেয়া আছে ডাটাসেট মেইনটেইনারের পক্ষ থেকে। না পড়লে বিপদে পড়বেন সামনে। অন্য কিছু না পড়লেও "Data Set Characteristics" এবং "Summary Statistics" পড়ে নেয়া জরুরি। print ব্যবহার করছি দেখার সুবিধার্থে। কি বুঝলেন? ভালো খবর হচ্ছে কোন ডাটা মিসিং নেই। এতো শান্তি কোথায় রাখবো! না হলে ওই ডাটা তৈরি করতে হতো টাইটানিকের মতো।
print(iris.DESCR)
মেশিন লার্নিং মডেলের জন্য কি দরকার?¶
দুটো জিনিস। তার আগে একটা ছবি দেখুন। এটা হচ্ছে সাইকিট-লার্ন এর ডাটা লেআউট। ধন্যবাদ, জেক ভ্যান্ডার প্লাসকে। মেশিন লার্নিং এর ভাষায় আমাদের দরকার ফিচার ম্যাট্রিক্স, আর টার্গেট ভেক্টর। সাইকিট-লার্ন আগে থেকে সেগুলোকে দুটো অ্যারে হিসেবে বানিয়ে রেখেছে। এখানে সেগুলোকে বলছি ডাটা অ্যারে আর টার্গেট অ্যারে।
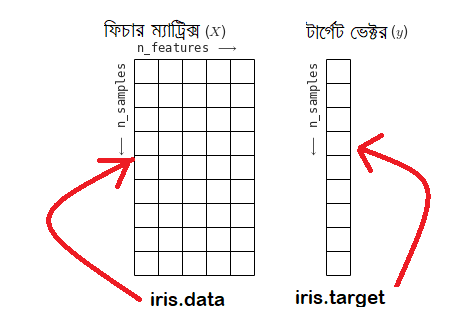
ফিচারগুলোর ম্যাট্রিক্স (X)¶
এবার নিচের ছবিটা দেখুন। দুই ডাইমেনশনাল আইরিস ফুলের মাপ্গুলো হচ্ছে ফিচার ম্যাট্রিক্স। সেটাকে মেলান ওপরের ছবিটার বামের টেবিলের সাথে। এই দুই ডাইমেনশনাল অ্যারেটার shape হচ্ছে [৯, ৫], যেটা এখানে [n_samples, n_features]। এখানে সারিগুলো হচ্ছে একেকটা স্যাম্পল অবজেক্ট ওই ডাটাসেটে। এখানে আইরিস ডাটাসেটের ৫০টা ফুলের ডাটা আছে এই ফিচার অ্যারেতে। চারটা ফিচার মানে চারটা মাপ আমাদের ফুলের। সেগুলো আছে কলাম ধরে। সাইকিট-লার্ন কনভেনশন অনুযায়ী এই অ্যারেকে স্টোর করে ভ্যারিয়েবল বড় 'X' এ। কেন? বলছি সামনে।
টার্গেট অ্যারে (y)¶
মডেলে ফিচারগুলোর ম্যাট্রিক্স (X) এর সাথে দরকার আমাদের টার্গেট অ্যারে, মানে আউটকাম ভ্যারিয়েবল। এটা সাধারণত: এক ডাইমেনশনাল হয়, লম্বা হয় ফিচারগুলোর ম্যাট্রিক্স (X) এর যতগুলো সারি থাকে। ওপরের ছবি অনুযায়ী অ্যারেটার shape হচ্ছে [৯, ১], যেটা এখানে [n_samples]। পরিসংখ্যানের ভাষায় এটা ডিপেন্ডেন্ট ভ্যারিয়েবল। কনভেনশন অনুযায়ী টার্গেট অ্যারেকে স্টোর করি টার্গেট অ্যারে (y)তে। লোয়ারকেস (y) হচ্ছে ডিপেনডেন্ট ভ্যারিয়েবল। অ্যারে (y) তার যেকোন পরিবর্তনের জন্য ফিচারগুলোর ম্যাট্রিক্স (X) এর ওপর নির্ভরশীল। এর মানে দাঁড়ালো ওই ফর্মুলার কথা। আমাদের অংকের ফাংশন অফ x, f(x)=y মানে ইনপুট x পাল্টালে আউটপুট y পাল্টাবে। বড় (X) ব্যবহার করার মানে হচ্ছে এটা হ্যান্ডেল করছে দুই ডাইমেনশনাল অ্যারে, আমরা যাকে বলছি ম্যাট্রিক্স। লোয়ারকেস y কারণ, আমাদের টার্গেট এক ডাইমেনশনাল অ্যারে, আমরা যাকে বলি ভেক্টর।
ডাটার শেপ, মানে কতোটা ইনস্ট্যান্স?¶
n_samples, n_features = iris.data.shape
n_samples
n_features
print("Shape of data:", iris['data'].shape)
কোন ডাটা মিসিং নেই
len(iris.target) == n_samples
ফিচারগুলোর নাম¶
ওপরের ছবিতে চারটা ফিচারের নাম দেখেছি। চলুন দেখি সেগুলো আমাদের ডাটাসেট অবজেক্টে। iris এর পর ডট নোটেশন ব্যবহার করে ডাকি একটা "কী" ভ্যালুকে। feature_names হচ্ছে আমাদের iris.keys() থেকে পাওয়া একটা অ্যাট্রিবিউট।
iris.feature_names
print(iris['feature_names'])
টার্গেট অর্থাৎ কী প্রেডিক্ট করতে চাই আমরা?¶
অনেকভাবেই করা সম্ভব। তবে print ফরম্যাটিং এ ভালো কাজ করে।
iris.target_names
print(iris.target_names)
list(iris.target_names)
print("Target names:", iris['target_names'])
কি আছে ডাটা অ্যারে আর টার্গেট অ্যারে এর ভেতর?¶
এখানে অ্যারে নিয়ে কাজ হচ্ছে। iris.dataতে সেই চারটা ১. পেটাল দৈর্ঘ্য, ২. পেটাল প্রস্থ, ৩. সিপাল দৈর্ঘ্য, ৪. সিপাল প্রস্থ মাপগুলো পাশাপাশি দেয়া আছে। শুরুতে দেখি প্রথম রেকর্ড। এরপর পুরো রেকর্ড।
iris.data[0]
iris.data
iris.target
আমাদের "ফিচার" আর "রেসপন্স" অর্থাৎ "টার্গেট" কি ধরণের কন্টেইনারে আছে, সেটা জানতে চাইলাম এখানে। ঠিক ধরেছেন। "নামপাই অ্যারে"।
print(type(iris.data))
print(type(iris.target))
ফিচারের ম্যাট্রিক্স কি? (১ম ডাইমেনশন = অবজার্ভেশনের সংখ্যা, ২য় = ফিচারের সংখ্যা)
print(iris.data.shape)
টার্গেট ম্যাট্রিক্স কি? (১ম ডাইমেনশন = লেবেল, টার্গেট, রেসপন্স)
print(iris.target.shape)
print("Shape of target:", iris['target'].shape)
সাইকিট-লার্ন এ ডাটা হ্যান্ডলিং এর নিয়ম¶
এখানে "ফিচার" এবং "রেসপন্স" দুটো আলাদা অবজেক্ট (আমাদের এখানে দেখুন, "ফিচার" এবং "রেসপন্স" মানে "টার্গেট" আলাদা অবজেক্ট)
"ফিচার" এবং "রেসপন্স" দুটোকেই সংখ্যা হতে হবে (আমাদের এখানে দুটোই সংখ্যার, দুটোর ম্যাট্রিক্স ডাইমেনশন হচ্ছে (১৫০ x ৪) এবং (১৫০ x ১)
"ফিচার" এবং "রেসপন্স" দুটোকেই "নামপাই অ্যারে" হতে হবে। (আমাদের দুটো ফিচারই আছে "নামপাই অ্যারে"তে, বাকি ডাটা ডাটাসেট দরকার হলে সেটাকেও লোড করে নিতে হবে "নামপাই অ্যারে"তে)
"ফিচার" এবং "রেসপন্স" দুটোকেই স্পেসিফিক shape হতে হবে
- ১৫০ x ৪ -> পুরো ডাটাসেট
- ১৫০ x ১ টার্গেটের জন্য
- ৪ x ১ ফিচারের জন্য
- আমরা ইচ্ছা করলে যেকোন ম্যাট্রিক্স পাল্টে নিতে পারি আমাদের দরকার মতো। যেমন np.tile(a, [4, 1]), মানে a হচ্ছে ম্যাট্রিক্স আর [4, 1] হচ্ছে ইনডেন্ট ম্যাট্রিক্স আরেক ডাইমেনশনে।
# ফিচার ম্যাট্রিক্স স্টোর করছি বড় "X"এ, মনে আছে f(x)=y কথা? x ইনপুট হলে y আউটপুট
X = iris.data
# রেসপন্স ভেক্টর রাখছি "y" তে
y = iris.target
X
y