Gradient Boosting: a practical guide¶
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
An example: the california housing dataset¶
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import median_absolute_error
calhousing = fetch_california_housing()
X, y = calhousing.data, calhousing.target
print(calhousing.DESCR)
.. _california_housing_dataset:
California Housing dataset
--------------------------
**Data Set Characteristics:**
:Number of Instances: 20640
:Number of Attributes: 8 numeric, predictive attributes and the target
:Attribute Information:
- MedInc median income in block
- HouseAge median house age in block
- AveRooms average number of rooms
- AveBedrms average number of bedrooms
- Population block population
- AveOccup average house occupancy
- Latitude house block latitude
- Longitude house block longitude
:Missing Attribute Values: None
This dataset was obtained from the StatLib repository.
http://lib.stat.cmu.edu/datasets/
The target variable is the median house value for California districts.
This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).
It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.
.. topic:: References
- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297
print(calhousing.feature_names)
['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=1000, random_state=0)
Let's start with a quick baseline model: linear regression (aka. Ordinary Least Squares):
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
%time lm = LinearRegression().fit(X_train, y_train)
CPU times: user 11.1 ms, sys: 1.11 ms, total: 12.2 ms Wall time: 8.61 ms
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, lm.predict(X_train)),
median_absolute_error(y_test, lm.predict(X_test))))
train error: 0.413, test error: 0.419
def scatter_predictions(y_pred, y_true):
plt.figure(figsize=(6, 6))
plt.xlabel('prediction')
plt.ylabel('true target')
plt.xlim(-1, 6)
plt.ylim(-1, 6)
plt.scatter(y_pred, y_true)
scatter_predictions(lm.predict(X_test), y_test)
This is pretty bad: the errors (off-diagonal predictions) seems to be heteroschedastic and there is a saturation effect with many samples with y_true == 5. Let's check:
plt.hist(y_train, bins=50);
We can filter out the "anomalies" and make the target variable marginal distribution more "Gaussian" by taking the log:
plt.hist(np.log(y_train), bins=50);
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.compose import TransformedTargetRegressor
from sklearn.pipeline import make_pipeline
lm2 = make_pipeline(
StandardScaler(),
TransformedTargetRegressor(LinearRegression(),
func=np.log, inverse_func=np.exp)
)
%time _ = lm2.fit(X_train, y_train)
CPU times: user 12.4 ms, sys: 2.77 ms, total: 15.2 ms Wall time: 14 ms
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, lm2.predict(X_train)),
median_absolute_error(y_test, lm2.predict(X_test))))
train error: 0.348, test error: 0.360
scatter_predictions(lm2.predict(X_test), y_test)
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import FunctionTransformer
plm = make_pipeline(
StandardScaler(),
PolynomialFeatures(degree=5),
TransformedTargetRegressor(LinearRegression(),
func=np.log, inverse_func=np.exp)
)
%time plm.fit(X_train, y_train)
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, plm.predict(X_train)),
median_absolute_error(y_test, plm.predict(X_test))))
CPU times: user 9.27 s, sys: 1.44 s, total: 10.7 s Wall time: 3.24 s train error: 0.217, test error: 0.235
scatter_predictions(plm.predict(X_test), y_test)
# from sklearn.neural_network import MLPRegressor
# mlp = make_pipeline(
# StandardScaler(),
# MLPRegressor(hidden_layer_sizes=(50, 50), activation='relu')
# )
# %time mlp.fit(X_train, y_train)
# print("train error: %0.3f, test error: %0.3f" %
# (median_absolute_error(y_train, mlp.predict(X_train)),
# median_absolute_error(y_test, mlp.predict(X_test))))
# scatter_predictions(mlp.predict(X_test), y_test)
from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(n_estimators=100, n_jobs=2)
%time _ = rfr.fit(X_train, y_train)
CPU times: user 12.5 s, sys: 71.4 ms, total: 12.6 s Wall time: 6.45 s
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, rfr.predict(X_train)),
median_absolute_error(y_test, rfr.predict(X_test))))
train error: 0.074, test error: 0.198
scatter_predictions(rfr.predict(X_test), y_test)
from pickle import dumps
print(f"Model size: {len(dumps(rfr)) / 1e6:.1f} MB")
Model size: 152.3 MB
X_test.shape
(1000, 8)
%timeit -n 3 rfr.predict(X_test)
147 ms ± 35 ms per loop (mean ± std. dev. of 7 runs, 3 loops each)
New Histogram-based Gradient Boosting Trees¶
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingRegressor
hgbr = HistGradientBoostingRegressor(max_leaf_nodes=256)
%time _ = hgbr.fit(X_train, y_train)
CPU times: user 12.3 s, sys: 254 ms, total: 12.6 s Wall time: 3.37 s
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, hgbr.predict(X_train)),
median_absolute_error(y_test, hgbr.predict(X_test))))
train error: 0.103, test error: 0.178
scatter_predictions(hgbr.predict(X_test), y_test)
print(f"Model size: {len(dumps(hgbr)) / 1e6:.1f} MB")
Model size: 2.4 MB
%timeit -n 10 hgbr.predict(X_test)
6.02 ms ± 3.62 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Early stopping¶
hgbr = HistGradientBoostingRegressor(max_leaf_nodes=256,
n_iter_no_change=10, validation_fraction=0.1,
scoring="loss", max_iter=10000)
%time _ = hgbr.fit(X_train, y_train)
CPU times: user 18.2 s, sys: 163 ms, total: 18.4 s Wall time: 4.97 s
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, hgbr.predict(X_train)),
median_absolute_error(y_test, hgbr.predict(X_test))))
train error: 0.080, test error: 0.172
hgbr.n_iter_
147
print("Model size: %0.1f MB" % (len(dumps(hgbr)) / 1e6))
Model size: 3.6 MB
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(hgbr.train_score_, label="train")
ax.plot(hgbr.validation_score_, "--", label="validation")
ax.set_xlabel("Boosting iteration (trees)")
ax.set_ylabel("Negative loss (MSE)")
ax.legend();
Explaining what the model learned¶
from sklearn.inspection.partial_dependence import plot_partial_dependence
features = [0, 5, 1, 2, (5, 1)]
plot_partial_dependence(hgbr, X_train, features,
feature_names=calhousing.feature_names,
n_jobs=-1, grid_resolution=50,
fig=plt.figure(figsize=(10, 9)))
fig.suptitle('Partial dependence of house value on nonlocation features\n'
'for the California housing dataset');
XGBoost and LightGBM¶
XGBoost and LightGBM provide efficient implementations with many features and a scikit-learn compatible interface.
They also support out-of-core and distributed model fitting although via a different API.
The new Histogram-based model of scikit-learn should be computationally competitive but (on single machine multithreads) but do not have all their features yet.
from xgboost import XGBRegressor
xgbr = XGBRegressor(learning_rate=0.1, max_depth=8, n_estimators=100)
%time xgbr.fit(X_train, y_train)
print("train error: %0.3f, test error: %0.3f" %
(median_absolute_error(y_train, xgbr.predict(X_train)),
median_absolute_error(y_test, xgbr.predict(X_test))))
%timeit -n 10 _ = xgbr.predict(X_test)
print("Model size: %0.1f MB" % (len(dumps(xgbr)) / 1e6))
Limitations¶
Regression with homogeneous feature interactions¶
Trees required to approximate X1−X2:
10 trees:
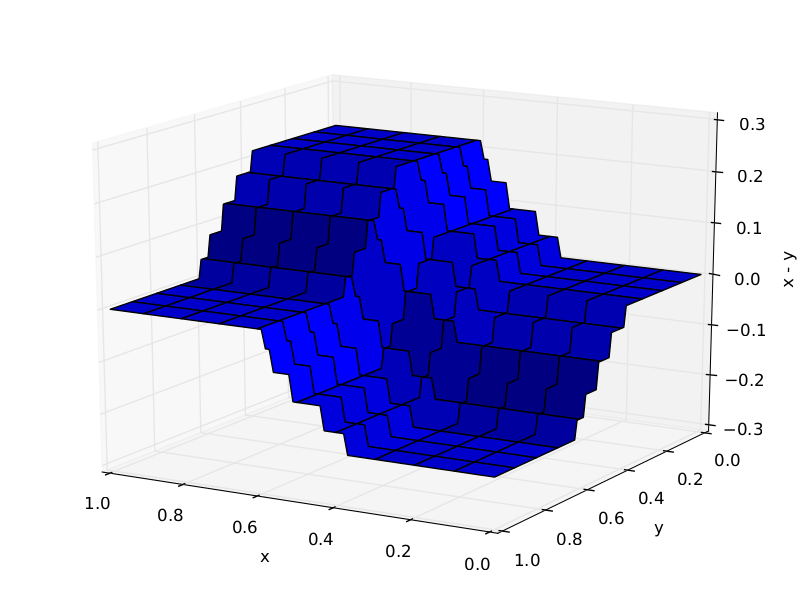
1000 trees:

Multiclass classification¶
The training time, model size and prediction latency of Gradient Boosted Trees scale linearly with the number of classes...
The following are possibly better models for multiclass classification with a large number of classes:
- Random Forests
- Linear models: multi-nomial logistic regression: might require extensive feature engineering to model non-linear interactions in original space. The nystroem method or polynomial features migth be useful in that case.
- Neural Networks (MLP)
High-dimensional feature spaces¶
GBRT models tend to work better on lower dimensional space (typically less than 500 features). Using feature importances or other feature selection strategies might help focus the feature engineering effort. But it cannot deal with very high dim bag of words feature for text classification for instance.
For very high-dimensional data, linear models will be much faster to train and possibly yield much better results. GBRT models can still be useful to blend predictions of other models, for instance:
- free text fields in database columns + few numeric or categorical fields
- train one TF-IDF (Bag of Words features) + logistic regression model per free-text field
- train a GBRT model that uses logistic regression models' probabilistic predictions concatenated with numerical and (integer coded) categorical fields to compute the final predictions.