Introduction¶
Learning outcomes¶
This Jupyter notebook will introduce the idea of pressure in the context of fluid mechanics. You will learn about the history of our understanding of pressure through the important measurements performed in the $17^{th}$ Century by an Anglo-Irish scientist. We will then delve deeper and look at some examples of the role of pressure in engineering flows.
The key areas are:
- Boyle's Law
- The Ideal Gas law
- Hydrostatics
- Pressure in moving fluids
Description of Pressure¶
Fundamental to fluid flow is the concept of pressure which is defined as the force per unit area ($N/m^2$) which is exerted by or on a fluid. We can think of many everyday examples that involve pressure; atmospheric pressure, tyre pressure, water pressure, exam pressure. But what causes pressure?
At the molecular scale we can describe pressure (and by extension temperature) according to kinetic theory. In the video below a cube containing particles is shown. These represent gas molecules and their kinetic energy as they randomly jostle about can be averaged into a quantity called temperature.
As the particles collide with the walls of the cube a force acting outward is observed. If we add more energy to the cube the particles motion will become more energetic and the pressure and temperature will increase. We observe this behaviour on the macro scale for example as a hot-air balloon is inflated or as a bicycle tyre gets warm as it is inflated.
On a larger scale again we experience the result of a pressure gradient as wind. Air will move from regions of the atmosphere at a higher pressure than their surroundings, perhaps due to solar heating, to regions of lower pressure. This relationship between pressure and flow velocity is extremely important in fluid mechanics and we will explore it in detail in this module.
Boyle's Law¶
Robert Boyle was born in Waterford in 1627 the fourteenth son of an English aristocrat, the first Earl of Cork. At age eight Boyle was sent to Eaton College in England and subsequently travelled around Europe developing an interest in the physical sciences. He settled in Dorset and begun to carry out a great many experiments. After a brief time in Ireland he moved to Oxford and, with his student Robert Hooke, begun to investigate the properties of air, in particular the 'spring of air'. Boyle and Hooke empirically observed (that is via experiment) that the volume of a gas varies inversely with the pressure of the gas. This observation became known as Boyle's Law.
Here is an image of his apparatus from the paper he published on this work [1]:
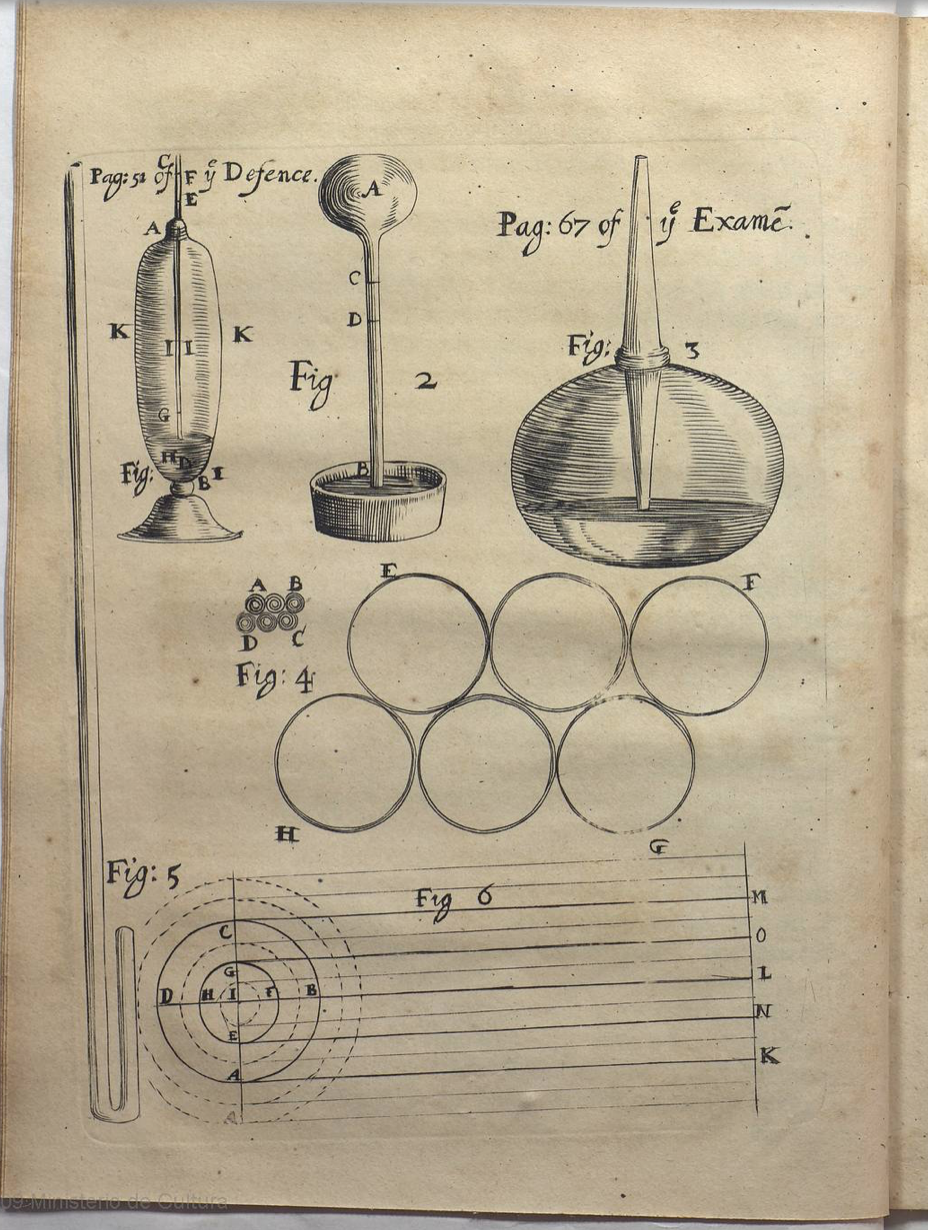
The apparatus consists of a glass tube in the shape of the letter 'J". The tube is closed at the short end and Boyle added mercury, a dense metal that is liquid at room temperature, to the open long end which resulted in the compression of the air trapped in the short end. Here are his actual data (yes, data is plural):

This can be a little hard to read, the letter 's' is written as 'f' for example, but the main point of the table is that as the volume of the air is reduced (columns A) the height of the mercury in the long leg increases. In column C Boyle notes the additional effect of atmospheric pressure, something we will cover a little later, and in Column D records the "preffure fuftained by the included air", i.e. the air trapped in the short end. Finally in column E he tests his hypothesis to show "what the preffure should be according to the Hypothefis, that fufposes the preffures and expanfions to be in reciprocal proportion". The result is in very good agreement!
Boyle use inches of mercury to measure the pressure and arbitrary marking on the glass to measure the air volume. Today we prefer to use SI units but lets work with the original data for now.
| Volume | Pressure |
|---|---|
| 48 | 29.125 |
| 46 | 30.5625 |
| 44 | 31.9375 |
| 42 | 33.5 |
| 40 | 35.3125 |
| 38 | 37 |
| 36 | 39.3125 |
| 34 | 41.625 |
| 32 | 44.1875 |
| 30 | 47.0625 |
| 28 | 50.3125 |
| 26 | 54.3125 |
| 24 | 58.8125 |
| 23 | 61.3125 |
| 22 | 64.0625 |
| 21 | 67.0625 |
| 20 | 70.6875 |
| 19 | 74.125 |
| 18 | 77.875 |
| 17 | 82.75 |
| 16 | 87.875 |
| 15 | 93.0625 |
| 14 | 100.4375 |
| 13 | 107.8125 |
| 12 | 117.5625 |
We can use python to plot the data and test the hypothesis.
\begin{equation} p \propto \frac{1}{V} \end{equation}or more concretely the product of pressure and volume is some constant $k$ that tells us something about the air's properties.
\begin{equation} {p}{V} = k \end{equation}where $k$ is a constant
# This is a Python cell. Juypter lets us run bits of code and see the results inline.
# Pressing SHIFT-ENTER in a Jupyter cell runs the contents of the cell.
# With Python we can import various libraries that offer additinal functionality as needed.
# Here we need to import some libraries that give Python Matlab like functinality.
# This means we can perform various calculations and tasks with matrices and vectors.
# The first is numpy which offers a lot of powerful numerical functions.
# These functions are prefixed with an 'np.' in the code becasue we tell Python
# to import the library numpy and thereafter refer to it as np for short.
import numpy as np
# Next we import the pyplot part of matplotlib and refer to it as 'plt'.
# This library lets us make varous types of plots just like in Matlab.
# As with numpy, matplotlib functions will pre prefixed by 'plt.'.
import matplotlib.pyplot as plt
# If you want to try and run this code elsewehere like in an interactive shell then ignore this next line.
# if you are using a Jupyter notebook as we are here then you need this line of code to make the plot show up below.
%matplotlib inline
# This line increases the resolution for Apple retina displays but also works well for 4K diplays.
%config InlineBackend.figure_format = 'retina'
# Define numpy arrays for our data
Volume = np.array([48, 46, 44, 42, 40, 38, 36, 34, 32, 30, 28, 26, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12])
Pressure = np.array([29.12500, 30.56250, 31.93750, 33.50000, 35.31250, 37.00000, 39.31250, 41.62500, 44.18750, 47.06250, 50.31250, 54.31250, 58.81250, 61.31250, 64.06250, 67.06250, 70.68750, 74.12500, 77.87500, 82.75000, 87.87500, 93.06250, 100.43750, 107.81250, 117.56250])
# Find the constant of proportionality between pressure and volume
k = Pressure * Volume
print(k)
k = np.mean(k)
plt.plot(Volume, Pressure,'bo')
plt.plot(Volume, k/Volume,'r-')
plt.xlabel('Volume (arbitary units)')
plt.ylabel('Pressure (arbitary units)')
print('k = '+str(k))
[1398. 1405.875 1405.25 1407. 1412.5 1406. 1415.25 1415.25 1414. 1411.875 1408.75 1412.125 1411.5 1410.1875 1409.375 1408.3125 1413.75 1408.375 1401.75 1406.75 1406. 1395.9375 1406.125 1401.5625 1410.75 ] k = 1408.09
plt.plot(Volume, 1/Pressure ,'bo')
plt.plot(Volume, Volume/k ,'r-')
plt.xlabel('Volume')
plt.ylabel('Pressure$^{-1}$')
print('Pressure is inversely proportional to volume')
Pressure is inversely proportional to volume
For the arbitrary units we see that $k = 1408.09$. Plotting the inverse of the pressure against the volume we obtain a straight line which means that the hypothesis is indeed valid, pressure is inversely proportional to volume. If we evaluate $k$ at any point along the data we should get the same answer. Therefore we can compute the change in pressure and volume from one condition to another for a constant $k$.
Now that Boyle's hypothesis has been tested we can write Boyle's Law as:
\begin{equation} {p_1}{V_1} = {p_2}{V_2} \end{equation}An Example¶
Lets do an example. We have a $1~m^3$ tank of compressed air at $300~kPa$. If we expand the gas into a $3~m^3$ container and ignore any temperature changes, what is the pressure of the air?
Invoking Boyle's law and entering our known data we have: \begin{align} {p_1}{V_1} = {p_2}{V_2} = {300,000}\times{1} = {p_2}\times{3} \end{align}
and solving for $p_2$: \begin{align} {p_2} = {300,000} / 3 = 100~kPa \end{align}
So we see that as we expand the gas to a larger volume the force (per unit area) the gas exerts on the walls of the container reduces. This also works in reverse, if we compress a volume of gas into a smaller container then the pressure will increase.
The Ideal Gas Law¶
Boyle's Law gives us a relationship between the pressure and volume of a gas. However what does the product ${p}{V} =k$ physically mean? While Boyle varied pressure and volume at a fixed temperature other scientists began to look at other combinations. What happens to pressure if you vary temperature but keep volume constant? (Gay-Lussac's law) What if you attempt to keep pressure constant but vary volume and temperature? (Charles's law) From these empirical observations a number of similar Laws were observed that relate the above relationships. The result is the ideal gas law:
\begin{equation} {p}{V} = n \mathrm{R} T \end{equation}Where $p$ and $V$ are our familiar pressure and volume, $T$ is the temperature, $\mathrm{R}$ is a universal gas constant and $n$ is the number of moles in the gas. Assuming that $\mathrm{R}$ and $n$ are constants this means that we now have a equation that describes the interrelationship between pressure, volume and temperature. We know from experience that if we heat a fixed volume of gas its pressure increases. Alternatively we can increase the volume of the container to maintain the pressure constant. You may even recognise the role of this equation in describing the operation of an internal combustion engine.
But what are $\mathrm{R}$ and $n$?
The latter is easy, $n$ is just the amount of stuff. The amount of gas molecules in our container. Chemists like to use moles as a measure of the amount of stuff because it allows them to make like for like comparisons in their reaction calculations. Like many other SI units the definition of the mole has changed recently. The current definition of a mole is exactly $6.022~140~76×10^{23}$ particles. Particles in this case are elementary entities such as atoms, ions, molecules, electrons etc. If I want to make pure water ${H_2}{O}$ I need to ensure I have twice as many Hydrogen atoms as Oxygen atoms. Hydrogen and Oxygen are stable in their $H_2$ and $O_2$ states so the chemical reaction is $2H_2 + O_2 \rightarrow 2{H_2}{O}$. I cannot completely react twice the mass of Hydrogen with Oxygen since it has a much smaller atomic mass than Oxygen, $1.008~g/mol$ vs $15.999~g/mol$. So the ratio is $(2\times1.008) : 15.999$ or about eight time as much oxygen to hydrogen by mass needed to satisfy our reaction equation.
Next is the universal gas constant $\mathrm{R}$. With units $J.K^{-1}.mol^{-1}$ the purpose of $\mathrm{R}$ is to relate the energy to the temperature scales that we have chosen. While convenient, many of our units are often arbitrary; the number of particles in a mole, the division of the temperature scale etc. The universal gas constant is found to be $\mathrm{R} = 8.31451~J.K^{-1}.mol^{-1}$
But as engineers we are less concerned about atoms and molecules. Instead we can write the ideal gas law in the form of a state equation using the specific gas constant $R_{\text{specific}} = \frac{\mathrm{R}}{M}$ where M is the molar mass ($g/mol$) of the species. We can replace $n$ with the ratio of the mass of the gas, $m$, in grams, to the molar mass in $g/mol$.
\begin{equation} n = \frac{m}{M} \end{equation}therefore
\begin{equation} pV = \frac{m}{M}{\mathrm{R}}{T} \end{equation}\begin{equation} pV = {m}\frac{\mathrm{R}}{M}{T} = {m}R_{\text{specific}} T \end{equation}which gives: \begin{equation} p = \frac{m}{V} R_{\text{specific}} T = \rho R_{\text{specific}} T \end{equation}
since the mass per unit volume is the density $\rho$. The specific gas constant for air is $287.05~J/Kg.K$.
Now we have a very useful equation that relates pressure, density (or mass and volume) and the temperature. We don't need to worry about the number of moles of our gas we just need to know its bulk properties. In Engineering we often refer to the specific gas constant as just $R$. Just be careful not to confuse it with the universal gas constant $\mathrm{R}$.
\begin{equation} p = \rho R T \end{equation}An Example¶
Lets do another example using the ideal gas law we've just derived with the help of Boyle's and other's data.
Air at sea level has a density of $1.225~kg/m^3$ and a pressure of $101.32~kPa$ (1 atmosphere). The specific gas constant of air is $287.05~J/kg.K$. What is the temperature at sea level?
p = 101.32e3 # Pa
rho = 1.225 # kg/m^3
R = 287.05 # J/kg.K
# Temperature
T = p/(rho * R)
# Print the result using an f-string
print(f"The temperature is {T:.2f} Kelvin, or {(T-273.15):.2f} degrees Celsius")
The temperature is 288.14 Kelvin, or 14.99 degrees Celsius
What happens to pressure as we increase altitude? What happens as we dive deep into the ocean?
The answer to these questions depends on the fluid. Gases, as we have seen already can be readily compressed. We can take a lot of natural gas and compress it into a small container. The air-fuel mixture in a car engine exploits this compression as part of its operation. Liquids on the other hand do not compress very much at all and for most cases we can assume that they are incompressible. This means that the density $\rho$ of the liquid doesn't change, no matter how much pressure we apply to it (note that it can change due to temperature too). For gases we can assume that they too are incompressible, within limits. This allows us to ignore changes in density for applications such as low-speed aerodynamics — such as for Formula One cars and light aircraft which makes engineering calculations much easier. However for high speed aircraft such as commercial airliners and military jets the effects of compressibility are significant and can result in very interesting flow physics.

As we increase altitude into the atmosphere the pressure and density both reduce. This is captured in the U.S. Standard atmosphere model available from http://www.pdas.com/atmos.html. This model is derived from equations we will study in this course including the Ideal Gas Law. Lets just plot the data for now.
Altitude = [-2.0, 0.0, 2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0, 18.0, 20.0, 22.0, 24.0, 26.0, 28.0, 30.0, 32.0, 34.0, 36.0, 38.0, 40.0, 42.0, 44.0, 46.0, 48.0, 50.0, 52.0, 54.0, 56.0, 58.0, 60.0, 62.0, 64.0, 66.0, 68.0, 70.0, 72.0, 74.0, 76.0, 78.0, 80.0, 82.0, 84.0, 86.0]
Temperature = [301.2, 288.1, 275.2, 262.2, 249.2, 236.2, 223.3, 216.6, 216.6, 216.6, 216.6, 216.6, 218.6, 220.6, 222.5, 224.5, 226.5, 228.5, 233.7, 239.3, 244.8, 250.4, 255.9, 261.4, 266.9, 270.6, 270.6, 269.0, 263.5, 258.0, 252.5, 247.0, 241.5, 236.0, 230.5, 225.1, 219.6, 214.3, 210.3, 206.4, 202.5, 198.6, 194.7, 190.8, 186.9]
Pressure = [1.278e+02, 1.013e+02, 7.950e+01, 6.166e+01, 4.722e+01, 3.565e+01, 2.650e+01, 1.940e+01, 1.417e+01, 1.035e+01, 7.565e+00, 5.529e+00, 4.047e+00, 2.972e+00, 2.188e+00, 1.616e+00, 1.197e+00, 8.890e-01, 6.634e-01, 4.985e-01, 3.771e-01, 2.871e-01, 2.200e-01, 1.695e-01, 1.313e-01, 1.023e-01, 7.977e-02, 6.221e-02, 4.833e-02, 3.736e-02, 2.872e-02, 2.196e-02, 1.669e-02, 1.260e-02, 9.459e-03, 7.051e-03, 5.220e-03, 3.835e-03, 2.800e-03, 2.033e-03, 1.467e-03, 1.052e-03, 7.498e-04, 5.308e-04, 3.732e-04]
Density = [1.478, 1.225, 1.007, 0.819, 0.660, 0.526, 0.413, 0.312, 0.228, 0.167, 0.122, 0.089, 0.065, 0.047, 0.034, 0.025, 0.018, 0.014, 0.010, 0.007, 0.005, 0.004, 0.003, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000]
plt.subplots(1,3,figsize=(10,10))
plt.subplot(131)
plt.plot(Temperature,Altitude,'k-')
plt.grid(True)
plt.ylabel('Altitude (km)')
plt.xlabel('Temperature (K)')
plt.text(250, 10, "Troposphere")
plt.text(250, 20, "Tropopause")
plt.text(250, 35, "Stratosphere")
plt.text(200, 50, "Mesosphere")
plt.subplot(132)
plt.plot(Pressure,Altitude,'k-')
plt.grid(True)
plt.xlabel('Pressure (kPa)')
plt.subplot(133)
plt.plot(Density,Altitude,'k-')
plt.grid(True)
plt.xlabel('Density ($kg/m^3$)')
print('International Standard Atmosphere model')
International Standard Atmosphere model
The model shows that both pressure and density reduce with some exponent as altitude increases. Temperature however initially drops linearly up to $10~km$ (referred to as the troposphere) before becoming stable from $10 – 20~km$ (in the tropopause) before slowly creeping up again (in the stratosphere) before falling linearly once more beyond $50~km$ (in the mesoshpere). In the troposphere the air is heated by the heat of the earth cooling with altitude. The temperature rise in the stratosphere is due to Ozone gas absorbing the sun's energy falling thereafter as the Ozone concentration reduces.
To reiterate, this foundational course in Fluid Mechanics is concerned with incompressible flow. We will assume the density doesn't change which is a reasonable assumption once we stay at a fixed altitude and don't exert significant force on our working fluids. All this discussion about the atmosphere is to provide an interesting introduction to the fluid that surrounds us!
Hydraulics¶
The use of liquids, particularly water, in many engineering applications is often referred to as hydraulics (air based systems are referred to as pneumatic). Here the incompressible nature of water or hydraulic oil is used to operate complex machinery. A common example is a hydraulic ram as shown in the video below. Hydraulic fluid pressurised (coloured red in the video) by a pump is used to push a piston attached to the ram arm along with the unpressurised fluid which is forced out of the chamber back to the supply reservoir. Such devices are used extensively in automotive applications such as brakes, and power steering. In aviation they are used to articulate control surfaces and in heavy machinery such as excavators and can deliver significant amounts of mechanical power.
Pneumatics¶
Pneumatic systems are similar to hydraulic systems but can incorporate a compressor pump to compress the ambient air and so are not reliant on a specialist fluid. Pneumatic systems are considered simpler and more reliable than hydraulic systems and are used extensively in systems where size and weight are more important than power. Examples of pneumatically powered systems include handheld power tools such as impact wrenches, high-speed CNC spindles, musical instruments and clean room equipment such as spin coaters.
Pressure and Depth — Hydrostatics¶
Another important aspect of Hydraulics is Hydrostatics and is concerned with the pressure exerted by a fluid (usually a liquid) with increasing depth. If the density of an incompressible fluid is constant, what happens when we compress it? We've actually already seen this in Boyle's experiment. He used mercury, which is a very dense liquid metal, to compress the air. The weight and height of the mercury column increased the pressure in the trapped gas. Another example is a deep sea diver experiencing increasing compression from the surrounding water the deeper they dive. To understand the effect of depth and pressure we need to consider Pascal's Law which states that the change in pressure $\Delta P$ is given by
where $g$ is acceleration due to gravity and $\Delta h$ is the height. As Boyle added more mercury of density $\rho$ to the open side of the J tube he increased $\Delta h$ the pressure experienced at the closed end of the tube increased under the weight of the dense fluid pushing down on it. The next three notebooks will discuss hydrostatics in some detail.
Measuring Pressure¶
As stated, pressure is the force exerted on or by a fluid per unit area. How do we go about quantifying it so we can use it precisely in engineering applications such as hydraulic rams or measure it accurately so we can perform tasks such as weather forecasting? There are many ways to measure pressure and they are often suited to particular fluids and applications. For example some fluids are corrosive and could damage fragile instruments. Sensors one would use for air may not be appropriate for water because of the electrical conductivity of the liquid. Some flows are very sensitive or precious such as biological flows so non-invasive methods are preferred. We will discuss several of these measurement methods throughout this course. These include manometers, Bourdon gauges, strain gauges and piezoelectric transducers. Some of these are used in conjunction with devices such as orifice plates and Venturi meters to measure flow velocity, which as we will see through a derivation of Bernoulli's Equation is as a result of pressure differences in fluids.
The Bourdon Pressure Gauge¶
The image below shows the fundamental operation of a Bourdon pressure gauge which is a common type of gauge in many engineering systems. You may be familiar with such a device from a tyre pump or an air compressor. The pressure in the vessel fills a tube with a closed end. The tube has a non-circular cross section and as a result undergoes an outward deflection when pressurised. This deflection is then amplified by a mechanical system to turn a needle pointer against a calibrated scale.
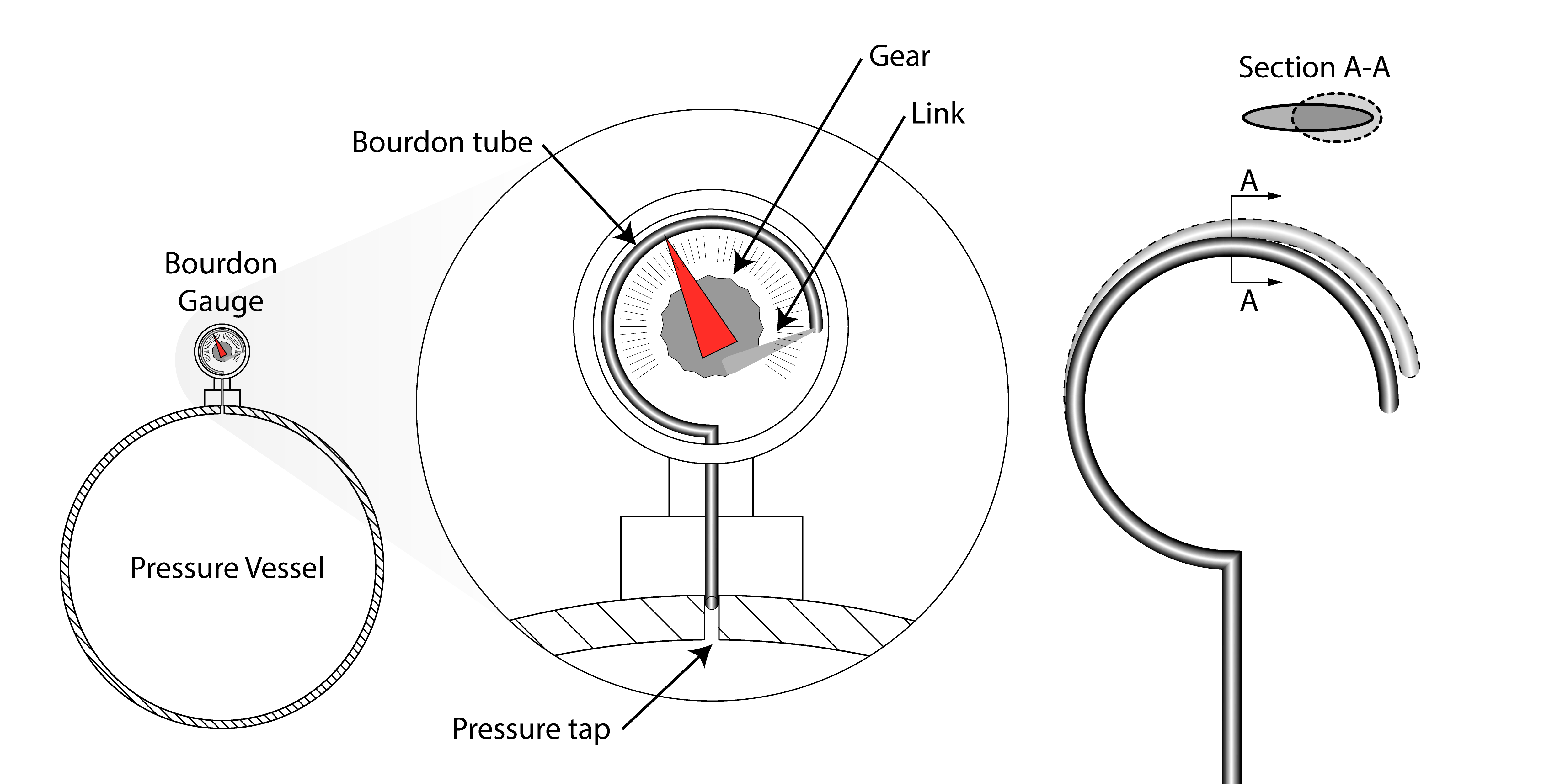
Static Pressure¶
Somewhat confusingly there are various other quantities that are also referred to as pressure, such as dynamic pressure and total pressure. These concern fluid in motion and incorporate the kinetic energy of the flow. The pressure described thus far we will refer to as the static pressure as it refers to the pressure of the fluid under static conditions.
A typical static pressure measurement is performed by attaching a suitable instrument to a static-pressure port or pressure tap on the vessel of interest. This is a small hole located normal to the surface where the fluid pressure at the point can me measured.
Absolute and Gauge Pressure¶
An important concept to understand right now is the idea of gauge pressure as this often confuses students and can lead to simple errors.
- The Absolute Pressure is the pressure measured relative to a Vacuum.
- The Gauge Pressure is the pressure measured relative to Atmospheric Pressure.
We live on a planet with an atmosphere and not in the vacuum of space. This means that we are subject to the static pressure due the height of the atmosphere above us and acceleration due to gravity. We calculated the sea level temperature earlier using the standard atmospheric pressure of $101.32 kPa = 1~atm$. If we have a pressure vessel, say a bicycle tube as (shown below) that we want to inflate, we would need to consider the pressure of the atmosphere on the outside and the pressure of the air within as these competing forces will determine how inflated the tube will be.
If there was a vacuum inside the tube the atmosphere would squish it flat as there is nothing inside to push outwards. We would struggle to move the tube walls relative to each other as the atmosphere pushes them together.
Opening the valve and allowing the atmosphere to rush in and equalise the tube would be more easily manipulated in our hands. We could roll the tube walls between our fingers but it would not be much use on our bike. The atmosphere now has no effect on the tube shape as it acts equally on the outside and the inside.
Using a pump to inflate the tube to a value of $600 kPa$ on the Bourdon gauge would result in an almost rigid torus. It is now very difficult to squish the tube and the rubber is now stretched tight. The pressure inside the tube is much higher than the atmosphere and the compressed air inside can push the tube wall out against the atmosphere.
- The Absolute Pressure inside the inflated tube is $600 + 101.32 = 701.32~kPa$. This is the pressure relative to a vacuum.
- The Absolute Pressure outside the tube is $101.32~kPa$. Again, this is the pressure relative to a vacuum.
- The Gauge Pressure inside the inflated tube is simply $600~kPa$ and is the pressure relative to our atmosphere.
- The Gauge Pressure outside the tube is simply $0~kPa$ and is the pressure relative to our atmosphere.
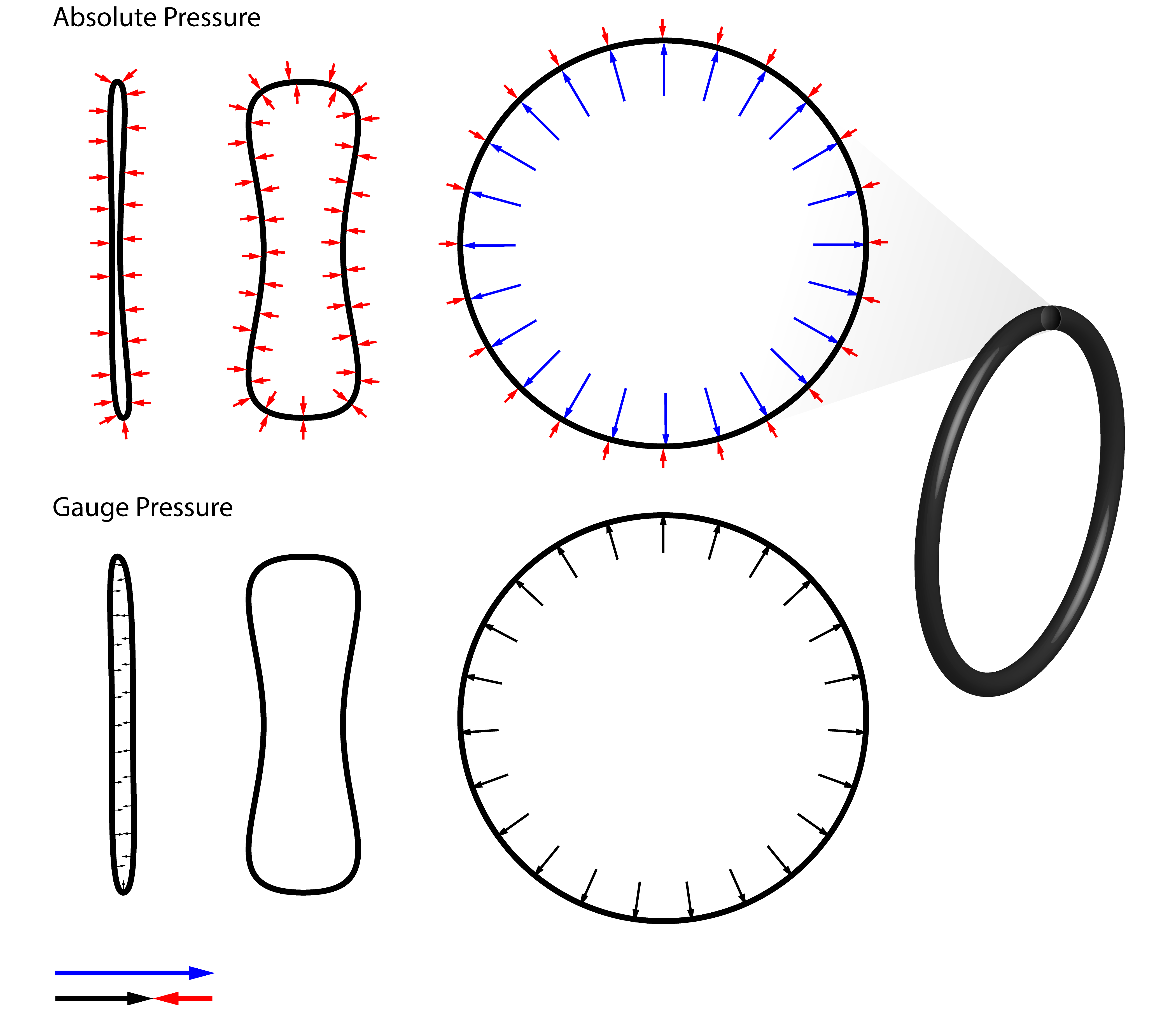
Pressure gauges which report gauge pressure are vented to the atmosphere. This means that they report the pressure relative to the ambient pressure which can change from day to day depending on metrological conditions or on altitude. Absolute pressure gauges are sealed so they can report pressure against a vacuum. Both types have their advantages and an engineer must select an appropriate instrument.
Take a look at an online vendor such as https://ie.rs-online.com/ and compare commerical gauges.
Vapour Pressure¶
Another quantity of interest is the vapour pressure. This is a measure of the evaporation of a substance in a closed container. At the molecular level, as we've seen in the video at the top of this notebook molecules are jostling about quite energetically. At this length scale the interface between a liquid and a gas (or a solid and a gas) is not so distinct. High energy molecules in the gas phase may impact the liquid phase and return to a lower energy state. Conversely molecules may be thrown off and join the high energy molecules in the gas phase. This process is continuously occurring.
A liquid placed in a sealed container with any empty space (a vacuum) and with no influences from outside (adiabatic) will eventually reach an equilibrium where the number of molecules entering the liquid phase is equal to those entering the gas phase. The gas molecules will fill any empty space. The pressure of the resulting gas phase in this equilibrium state is the vapour pressure.
Some liquids are more volatile than others and this is why you can smell pungent liquids like alcohol and ammonia which readily evaporate at room temperature. A open container of a volatile liquid like ethanol will evaporate to the environment in a few minutes. Other liquids like mercury and various silicon oils have much lower vapour pressures and evaporate at much slower rates.
For mixtures of gases there is the concept of partial pressures but this is beyond the scope of this course.
Measuring Pressure¶
There are various instruments, including the Bourdon Gauge, that are commonly employed to measure pressure. This include:
- Mercury barometer
- Aneroid Barometer
- MEMS — Smartphones
- Manometer
- Piezoelectric diaphragm
As we will see later Bernoulli's equation allows us to relate pressure and flow velocity. There are additional instruments that also measure pressure to provide a velocity measurement.
- Pitot static tube
- Venturi meter
- Orifice plate
We will explore several of these instruments during this course.
References¶
- Boyle, R., 1662, "A defence of the doctrine touching the spring and weight of the air", The works of Robert Boyle
- Munson, B.R., Young, D.F., Okiishi, T.H. and Huebsch, W.W., 2010. "Fundamentals of Fluid Mechanics". Singapore: Wiley.