In [1]:
import numpy as np
import random
In [2]:
import import_ipynb
from q1_softmax import softmax
from q2_sigmoid import sigmoid, sigmoid_grad
from q2_gradcheck import gradcheck_naive
importing Jupyter notebook from q1_softmax.ipynb importing Jupyter notebook from q2_sigmoid.ipynb importing Jupyter notebook from q2_gradcheck.ipynb
backward¶
$\delta_1 = \frac{\partial{CE}}{\partial{z_2}} = \hat{y} - y$
$\begin{align} \delta_2 = \frac{\partial{CE}}{\partial{h}} = \frac{\partial{CE}}{\partial{z_2}} \frac{\partial{z_2}}{\partial{h}} = \delta_1W_2^T \end{align}$
$\begin{align}\delta_3 = \frac{\partial{CE}}{z_1} = \frac{\partial{CE}}{\partial{h}}\frac{\partial{h}}{\partial{z_1}} = \delta_2 \frac{\partial{h}}{\partial{z_1}}= \delta_2 \circ \sigma'(z_1)\end{align}$
$\frac{\partial{CE}}{\partial{x}}=\delta_3\frac{\partial{z_1}}{\partial{x}} = \delta_3W_1^T $
In [3]:
def forward_backward_prop(data, labels, params, dimensions):
"""
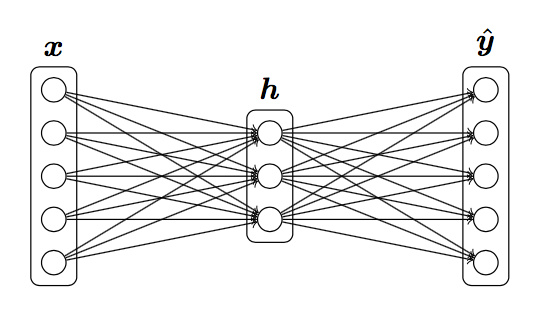
Forward and backward propagation for a two-layer sigmoidal network
Compute the forward propagation and for the cross entropy cost,
and backward propagation for the gradients for all parameters.
Arguments:
data -- M x Dx matrix, where each row is a training example.
labels -- M x Dy matrix, where each row is a one-hot vector.
params -- Model parameters, these are unpacked for you.
dimensions -- A tuple of input dimension, number of hidden units
and output dimension
"""
### Unpack network parameters (do not modify)
ofs = 0
Dx, H, Dy = (dimensions[0], dimensions[1], dimensions[2])
W1 = np.reshape(params[ofs:ofs+ Dx * H], (Dx, H))
ofs += Dx * H
b1 = np.reshape(params[ofs:ofs + H], (1, H))
ofs += H
W2 = np.reshape(params[ofs:ofs + H * Dy], (H, Dy))
ofs += H * Dy
b2 = np.reshape(params[ofs:ofs + Dy], (1, Dy))
### YOUR CODE HERE: forward propagation
h = sigmoid(np.dot(data,W1) + b1)
yhat = softmax(np.dot(h,W2) + b2)
### END YOUR CODE
### YOUR CODE HERE: backward propagation
cost = np.sum(-np.log(yhat[labels==1]))
d1 = (yhat - labels)
gradW2 = np.dot(h.T, d1)
gradb2 = np.sum(d1,0,keepdims=True)
d2 = np.dot(d1,W2.T)
# h = sigmoid(z_1)
d3 = sigmoid_grad(h) * d2
gradW1 = np.dot(data.T,d3)
gradb1 = np.sum(d3,0)
### END YOUR CODE
### Stack gradients (do not modify)
grad = np.concatenate((gradW1.flatten(), gradb1.flatten(),
gradW2.flatten(), gradb2.flatten()))
return cost, grad
In [4]:
def sanity_check():
"""
Set up fake data and parameters for the neural network, and test using
gradcheck.
"""
print("Running sanity check...")
N = 20
dimensions = [10, 5, 10]
data = np.random.randn(N, dimensions[0]) # each row will be a datum
labels = np.zeros((N, dimensions[2]))
for i in range(N):
labels[i, random.randint(0,dimensions[2]-1)] = 1
params = np.random.randn((dimensions[0] + 1) * dimensions[1] + (
dimensions[1] + 1) * dimensions[2], )
gradcheck_naive(lambda params:
forward_backward_prop(data, labels, params, dimensions), params)
if __name__ == "__main__":
sanity_check()
Running sanity check... Gradient check passed!
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]: