
Filtration¶
Filtration is used to highlight an information and suppress the noise. It is dependent on type of the solved task.
Filtration with more images¶


Výsledek po průměrování

Local averaging - convolution¶
%pylab inline --no-import-all
import numpy as np
import scipy
from scipy import ndimage
import scipy.signal
import scipy.misc
import skimage.data
import skimage.io
import matplotlib.pyplot as plt
Populating the interactive namespace from numpy and matplotlib
# plt.imshow(scipy.misc.lena())
plt.imshow(skimage.data.astronaut())
<matplotlib.image.AxesImage at 0x1f43b7d1dd8>
Convolution¶
np.convolve([3, 10, 10, 1, 2, 2], [1, -2, 1])
array([ 3, 4, -7, -9, 10, -1, -2, 2])

np.convolve([10, 10, 10, 10, 10, 10, 10, 10], [1, -2, 1], "valid")
array([0, 0, 0, 0, 0, 0])
np.convolve([10, 10, 10, 10, 10, 0, 0, 0, 0, 0], [1, -2, 1], "valid")
array([ 0, 0, 0, -10, 10, 0, 0, 0])
Colvolution 2D¶

lena = skimage.io.imread("https://i.stack.imgur.com/3T6Gc.jpg")
plt.imshow(lena)
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x21e4b55afd0>
# lena = scipy.misc.face()
# l = lena[250:340, 530:630,0]
lena = skimage.io.imread("https://i.stack.imgur.com/3T6Gc.jpg", as_grey=True)
# print(lena.max())
l = lena[230:290, 220:320]
noisy = l + 1.6*l.std()*np.random.random(l.shape)
print(noisy.std())
plt.imshow(noisy, cmap='gray', interpolation=None)
#plt.imshow(lena)
plt.colorbar()
plt.show()
0.20064397202412135
import scipy.signal
kernel = np.ones([15,15])
output1 = scipy.signal.convolve2d(noisy, kernel)
plt.imshow(output1, cmap="gray")
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x21e49ef5080>
kernel = np.ones([15,15])
kernel = kernel / np.sum(kernel)
output1 = scipy.signal.convolve2d(noisy, kernel)
plt.imshow(output1, cmap="gray")
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x21e49f8c0b8>
Covolution behind borders¶
import scipy.signal
kernel = np.ones([15,15])
output1 = scipy.signal.convolve2d(noisy, kernel, boundary="fill", fillvalue=0)
output2 = scipy.signal.convolve2d(noisy, kernel, boundary="wrap")
output3 = scipy.signal.convolve2d(noisy, kernel, boundary="symm")
plt.figure(figsize=[10,15])
plt.subplot(131)
plt.imshow(output1, cmap="gray")
plt.subplot(132)
plt.imshow(output2, cmap="gray")
plt.subplot(133)
plt.imshow(output3, cmap="gray")
<matplotlib.image.AxesImage at 0x21e4a186f60>
Convolution size¶
import scipy.signal
kernel = np.ones([15,15])
output1 = scipy.signal.convolve2d(noisy, kernel, mode="full", boundary="fill")
output2 = scipy.signal.convolve2d(noisy, kernel, mode="same", boundary="fill")
output3 = scipy.signal.convolve2d(noisy, kernel, mode="valid", boundary="fill")
plt.figure(figsize=[10,15])
plt.subplot(131)
plt.imshow(output1, cmap="gray")
plt.subplot(132)
plt.imshow(output2, cmap="gray")
plt.subplot(133)
plt.imshow(output3, cmap="gray")
<matplotlib.image.AxesImage at 0x21e4a25be48>
local_mean = ndimage.uniform_filter(noisy, size=15)
plt.imshow(local_mean, cmap='gray', interpolation=None)
plt.show()
Gaussian filter¶
blurred_lena = ndimage.gaussian_filter(noisy, sigma=1)
very_blurred = ndimage.gaussian_filter(noisy, sigma=5)
plt.imshow(blurred_lena, cmap='gray')
plt.figure()
plt.imshow(very_blurred, cmap='gray')
<matplotlib.image.AxesImage at 0x21e4b54b518>
Remove noise¶
Zašumněný obraz odstranění šumu




Non-linear filters¶
Quantiles (median)¶
med_denoised = ndimage.median_filter(noisy, 3)
plt.imshow(noisy, cmap='gray')
plt.show()
plt.figure()
plt.imshow(med_denoised, cmap='gray')
plt.show()
Other filters¶
Další kvantilové filtry
ndimage.maximum_filter, ndimage.percentile_filter
Nelineární filtry
scipy.signal.wiener
Gradient filters¶
import scipy
import scipy.ndimage
import matplotlib.pyplot as plt
Sobel¶
img = np.zeros([50, 50])
img[20:30,20:30] = 50
plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.subplot(122)
sob = scipy.ndimage.filters.sobel(img, 0)
plt.imshow(sob, cmap='gray')
<matplotlib.image.AxesImage at 0x229d84beac8>
img = np.zeros([50,50,50])
img[20:30,20:30,20:30] = 50
plt.subplot(121)
plt.imshow(img[:,:,20], cmap='gray')
plt.subplot(122)
sob = scipy.ndimage.filters.sobel(img,2)
plt.imshow(sob[:,:,20], cmap='gray')
<matplotlib.image.AxesImage at 0x229d8573470>
edg_sobel = skimage.filter.sobel(image)
plt.imshow(edg_sobel, cmap='gray')
<matplotlib.image.AxesImage at 0x7f767d3b9dd0>
Roberts¶
import matplotlib.pyplot as plt
import skimage.data
import skimage.filter
# import roberts, sobel
image = skimage.data.camera()
edge_roberts = skimage.filter.roberts(image)
plt.imshow(edge_roberts, cmap='gray')
<matplotlib.image.AxesImage at 0x7f767d47fa50>
import pylab as pl
sx=ndimage.sobel(image,axis=0,mode='constant')
sy=ndimage.sobel(image,axis=1,mode='constant')
# sob=np.hypot(sx,sy)
# pl.quiver(sx, sy)
plt.imshow(sx)
plt.figure()
plt.imshow(sy)
<matplotlib.image.AxesImage at 0x7f767c085050>
from scipy import ndimage
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im = ndimage.rotate(im, 15, mode='constant')
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis=0, mode='constant')
sy = ndimage.sobel(im, axis=1, mode='constant')
sob = np.hypot(sx, sy)
plt.figure(figsize=(16, 5))
plt.subplot(141)
plt.imshow(im, cmap=plt.cm.gray)
plt.axis('off')
plt.title('square', fontsize=20)
plt.subplot(142)
plt.imshow(sx)
plt.axis('off')
plt.title('Sobel (x direction)', fontsize=20)
plt.subplot(143)
plt.imshow(sob)
plt.axis('off')
plt.title('Sobel filter', fontsize=20)
im += 0.07*np.random.random(im.shape)
sx = ndimage.sobel(im, axis=0, mode='constant')
sy = ndimage.sobel(im, axis=1, mode='constant')
sob = np.hypot(sx, sy)
plt.subplot(144)
plt.imshow(sob)
plt.axis('off')
plt.title('Sobel for noisy image', fontsize=20)
plt.subplots_adjust(wspace=0.02, hspace=0.02, top=1, bottom=0, left=0, right=0.9)
plt.show()
Laplace¶
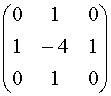
Canny¶
edges2 = skimage.filter.canny(image, sigma=3)
plt.imshow(edges2, cmap='gray')
<matplotlib.image.AxesImage at 0x7f76740fa650>
Example of filtration use¶
Odstranění vlivu nerovnoměrného osvětlen. Tuto operaci lze provádět pouze pro případy, kdy pozadí zabírá velkou část obrazu a je možné odstranit objekty pomocí filtrace. Příklad:

vlevo nahoře – šedotónový obraz se světelným přechodem, vpravo nahoře naprahovaný obraz pomocí prahu 150 (struktura není znatelná na celém obraze), vlevo dole – původní obraz po odstranění objektů, vpravo dole – výsledek prahování po odstranění vlivu pozadí (odečtení od původního obrazu)
Exercise¶
Get the gradient image without dot-like noise
import cv2
import numpy as np
from matplotlib import pyplot as plt
import scipy
import scipy.misc
import urllib
import cStringIO
import matplotlib.pyplot as plt
import scipy.ndimage
from scipy import ndimage
import skimage
import skimage.io
# scipy.misc.imread(
URL = "http://uc452cam01-kky.fav.zcu.cz/snapshot.jpg"
img = skimage.io.imread(URL)
plt.imshow(img)
<matplotlib.image.AxesImage at 0x7f765d728a10>
Test¶
V testu očekávejte otázky typu: Co je to hrana? Jaké typy nelinearni filtrace znáte? Nakreslete transformační funkci pro zesvětlení obrazu apod.
Úkoly¶
definujte co je to hrana v obraze
vyzkoušejte jak funguje třetí parametr (práh) u funkce edge
naprogramujte výpočet diferencí v ose x a y z daného šedotónového obrazu, z těchto hodnot vypočítejte velikost hrany a její směr pro každý bod obrazu, zobrazte velikost hran pomocí imshow, proveďte naprahování velikostí hran na nějakou hodnotu (stejny vysledek jako edge), vykreslete si velikost a směr hran pomocí funkce quiver (dx(diference v x),dy(diference v y))
vyzkoušejte odstranění vlivu osvětlení na obraze mince.jpg, (nejprve je nutné do obrazu osvětlení přidat)
Úkoly na cvičení¶
- Spočítat objekty v obraze
- Spočítat velké objekty v obraze, je-li přidán šum v podobě malých útržků papíru

