Gradient Descent¶
1. Gradient¶
In [57]:
import numpy as np
import matplotlib.pylab as plt
In [58]:
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01*x**2 + 0.1*x
def tangent_line(f, x):
d = numerical_diff(f, x)
return lambda t: d * (t - x) + f(x)
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
tf = tangent_line(function_1, 5)
y2 = tf(x)
plt.plot(x, y)
plt.plot(x, y2)
plt.show()
2. Implement Gradient Descent in Python¶
In [103]:
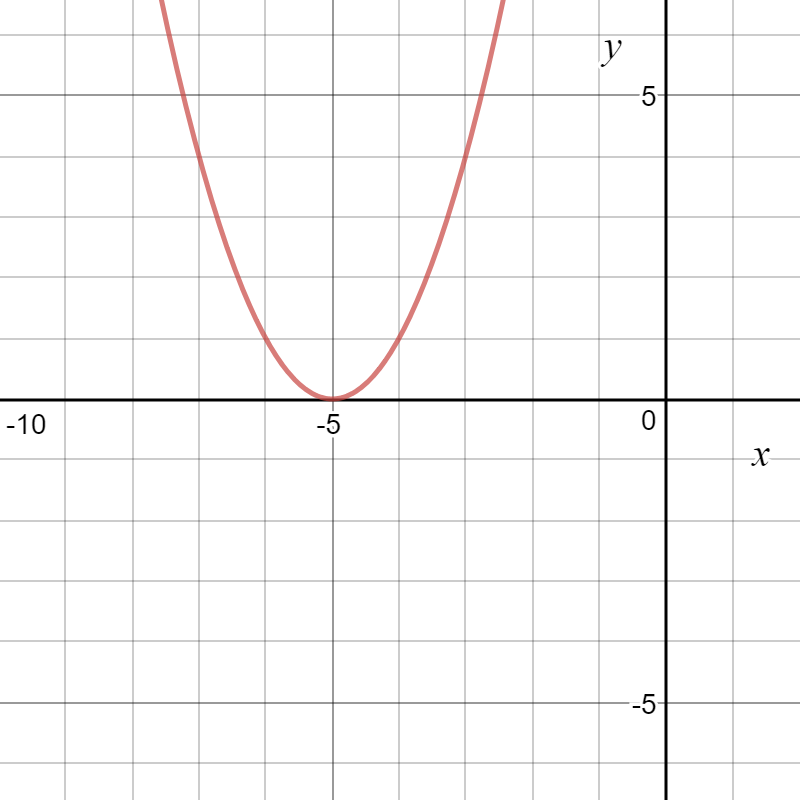
f = lambda x: (x + 5)**2
from IPython.display import Image
Image(url= "https://cdn-images-1.medium.com/max/800/1*5-56UEwcZHgzqIAtlnsLog.png", width=300, height=300)
Out[103]:
- Step 1 : Initialize parameters
In [108]:
f = lambda x: (x + 5)**2
cur_x = 3 # The algorithm starts at x=3
learning_rate = 0.1 # Learning rate
precision = 0.000001 #This tells us when to stop the algorithm
previous_step_size = 1 #
max_iters = 10000 # maximum number of iterations
iters = 0 #iteration counter
df = lambda x: 2 * (x + 5) #Gradient of our function
- Step 2 : Run a loop to perform gradient descent
- Stop loop when difference between x values from 2 consecutive iterations is less than 0.000001 or when number of iterations exceeds 10,000
In [109]:
print("Iteration: {0:2d} - X is {1:8.5f}".format(0, cur_x))
while previous_step_size > precision and iters < max_iters:
prev_x = cur_x #Store current x value in prev_x
cur_x = cur_x - learning_rate * df(prev_x) #Grad descent
previous_step_size = abs(cur_x - prev_x) #Change in x
iters = iters + 1 #iteration count
print("Iteration: {0:2d} - X value is {1:8.5f}".format(iters, cur_x)) #Print iterations
print("The local minimum occurs at {0:8.5f}".format(cur_x))
Iteration: 0 - X is 3.00000 Iteration: 1 - X value is 1.40000 Iteration: 2 - X value is 0.12000 Iteration: 3 - X value is -0.90400 Iteration: 4 - X value is -1.72320 Iteration: 5 - X value is -2.37856 Iteration: 6 - X value is -2.90285 Iteration: 7 - X value is -3.32228 Iteration: 8 - X value is -3.65782 Iteration: 9 - X value is -3.92626 Iteration: 10 - X value is -4.14101 Iteration: 11 - X value is -4.31281 Iteration: 12 - X value is -4.45024 Iteration: 13 - X value is -4.56020 Iteration: 14 - X value is -4.64816 Iteration: 15 - X value is -4.71853 Iteration: 16 - X value is -4.77482 Iteration: 17 - X value is -4.81986 Iteration: 18 - X value is -4.85588 Iteration: 19 - X value is -4.88471 Iteration: 20 - X value is -4.90777 Iteration: 21 - X value is -4.92621 Iteration: 22 - X value is -4.94097 Iteration: 23 - X value is -4.95278 Iteration: 24 - X value is -4.96222 Iteration: 25 - X value is -4.96978 Iteration: 26 - X value is -4.97582 Iteration: 27 - X value is -4.98066 Iteration: 28 - X value is -4.98453 Iteration: 29 - X value is -4.98762 Iteration: 30 - X value is -4.99010 Iteration: 31 - X value is -4.99208 Iteration: 32 - X value is -4.99366 Iteration: 33 - X value is -4.99493 Iteration: 34 - X value is -4.99594 Iteration: 35 - X value is -4.99675 Iteration: 36 - X value is -4.99740 Iteration: 37 - X value is -4.99792 Iteration: 38 - X value is -4.99834 Iteration: 39 - X value is -4.99867 Iteration: 40 - X value is -4.99894 Iteration: 41 - X value is -4.99915 Iteration: 42 - X value is -4.99932 Iteration: 43 - X value is -4.99946 Iteration: 44 - X value is -4.99956 Iteration: 45 - X value is -4.99965 Iteration: 46 - X value is -4.99972 Iteration: 47 - X value is -4.99978 Iteration: 48 - X value is -4.99982 Iteration: 49 - X value is -4.99986 Iteration: 50 - X value is -4.99989 Iteration: 51 - X value is -4.99991 Iteration: 52 - X value is -4.99993 Iteration: 53 - X value is -4.99994 Iteration: 54 - X value is -4.99995 Iteration: 55 - X value is -4.99996 Iteration: 56 - X value is -4.99997 Iteration: 57 - X value is -4.99998 Iteration: 58 - X value is -4.99998 Iteration: 59 - X value is -4.99998 Iteration: 60 - X value is -4.99999 Iteration: 61 - X value is -4.99999 Iteration: 62 - X value is -4.99999 Iteration: 63 - X value is -4.99999 Iteration: 64 - X value is -4.99999 Iteration: 65 - X value is -5.00000 Iteration: 66 - X value is -5.00000 The local minimum occurs at -5.00000
3. Implement 2D Gradient Descent in Python¶
In [110]:
f = lambda x, y: x ** 2 + y ** 2 + 10
cur_x = 3 # The algorithm starts at x=3
cur_y = -3 # The algorithm starts at y=-3
learning_rate = 0.1 # Learning rate
precision = 0.000001 #This tells us when to stop the algorithm
previous_step_size = 1 #
max_iters = 10000 # maximum number of iterations
iters = 0 #iteration counter
df_x = lambda x, y: 2 * x #Gradient of our function for x
df_y = lambda x, y: 2 * y #Gradient of our function for y
In [111]:
print("Iteration: {0:2d} - X is {1:8.5f}, Y is {2:8.5f},".format(0, cur_x, cur_y))
while previous_step_size > precision and iters < max_iters:
prev_x = cur_x #Store current x value in prev_x
prev_y = cur_y #Store current x value in prev_x
cur_x = cur_x - learning_rate * df_x(prev_x, prev_y) #Grad descent for x
cur_y = cur_y - learning_rate * df_y(prev_x, prev_y) #Grad descent for x
previous_step_size = abs(cur_x - prev_x) + abs(cur_y - prev_y) #Change in x
iters = iters + 1 #iteration count
print("Iteration: {0:2d} - X is {1:8.5f}, Y is {2:8.5f},".format(iters, cur_x, cur_y)) #Print iterations
print("The local minimum occurs at {0:8.5f}, {1:8.5f}".format(cur_x, cur_y))
Iteration: 0 - X is 3.00000, Y is -3.00000, Iteration: 1 - X is 2.40000, Y is -2.40000, Iteration: 2 - X is 1.92000, Y is -1.92000, Iteration: 3 - X is 1.53600, Y is -1.53600, Iteration: 4 - X is 1.22880, Y is -1.22880, Iteration: 5 - X is 0.98304, Y is -0.98304, Iteration: 6 - X is 0.78643, Y is -0.78643, Iteration: 7 - X is 0.62915, Y is -0.62915, Iteration: 8 - X is 0.50332, Y is -0.50332, Iteration: 9 - X is 0.40265, Y is -0.40265, Iteration: 10 - X is 0.32212, Y is -0.32212, Iteration: 11 - X is 0.25770, Y is -0.25770, Iteration: 12 - X is 0.20616, Y is -0.20616, Iteration: 13 - X is 0.16493, Y is -0.16493, Iteration: 14 - X is 0.13194, Y is -0.13194, Iteration: 15 - X is 0.10555, Y is -0.10555, Iteration: 16 - X is 0.08444, Y is -0.08444, Iteration: 17 - X is 0.06755, Y is -0.06755, Iteration: 18 - X is 0.05404, Y is -0.05404, Iteration: 19 - X is 0.04323, Y is -0.04323, Iteration: 20 - X is 0.03459, Y is -0.03459, Iteration: 21 - X is 0.02767, Y is -0.02767, Iteration: 22 - X is 0.02214, Y is -0.02214, Iteration: 23 - X is 0.01771, Y is -0.01771, Iteration: 24 - X is 0.01417, Y is -0.01417, Iteration: 25 - X is 0.01133, Y is -0.01133, Iteration: 26 - X is 0.00907, Y is -0.00907, Iteration: 27 - X is 0.00725, Y is -0.00725, Iteration: 28 - X is 0.00580, Y is -0.00580, Iteration: 29 - X is 0.00464, Y is -0.00464, Iteration: 30 - X is 0.00371, Y is -0.00371, Iteration: 31 - X is 0.00297, Y is -0.00297, Iteration: 32 - X is 0.00238, Y is -0.00238, Iteration: 33 - X is 0.00190, Y is -0.00190, Iteration: 34 - X is 0.00152, Y is -0.00152, Iteration: 35 - X is 0.00122, Y is -0.00122, Iteration: 36 - X is 0.00097, Y is -0.00097, Iteration: 37 - X is 0.00078, Y is -0.00078, Iteration: 38 - X is 0.00062, Y is -0.00062, Iteration: 39 - X is 0.00050, Y is -0.00050, Iteration: 40 - X is 0.00040, Y is -0.00040, Iteration: 41 - X is 0.00032, Y is -0.00032, Iteration: 42 - X is 0.00026, Y is -0.00026, Iteration: 43 - X is 0.00020, Y is -0.00020, Iteration: 44 - X is 0.00016, Y is -0.00016, Iteration: 45 - X is 0.00013, Y is -0.00013, Iteration: 46 - X is 0.00010, Y is -0.00010, Iteration: 47 - X is 0.00008, Y is -0.00008, Iteration: 48 - X is 0.00007, Y is -0.00007, Iteration: 49 - X is 0.00005, Y is -0.00005, Iteration: 50 - X is 0.00004, Y is -0.00004, Iteration: 51 - X is 0.00003, Y is -0.00003, Iteration: 52 - X is 0.00003, Y is -0.00003, Iteration: 53 - X is 0.00002, Y is -0.00002, Iteration: 54 - X is 0.00002, Y is -0.00002, Iteration: 55 - X is 0.00001, Y is -0.00001, Iteration: 56 - X is 0.00001, Y is -0.00001, Iteration: 57 - X is 0.00001, Y is -0.00001, Iteration: 58 - X is 0.00001, Y is -0.00001, Iteration: 59 - X is 0.00001, Y is -0.00001, Iteration: 60 - X is 0.00000, Y is -0.00000, Iteration: 61 - X is 0.00000, Y is -0.00000, Iteration: 62 - X is 0.00000, Y is -0.00000, Iteration: 63 - X is 0.00000, Y is -0.00000, Iteration: 64 - X is 0.00000, Y is -0.00000, The local minimum occurs at 0.00000, -0.00000
In [ ]: