-----------------------------------------------------------------------------------------------------------------------------¶
A Disarium number is a number defined by the following process:
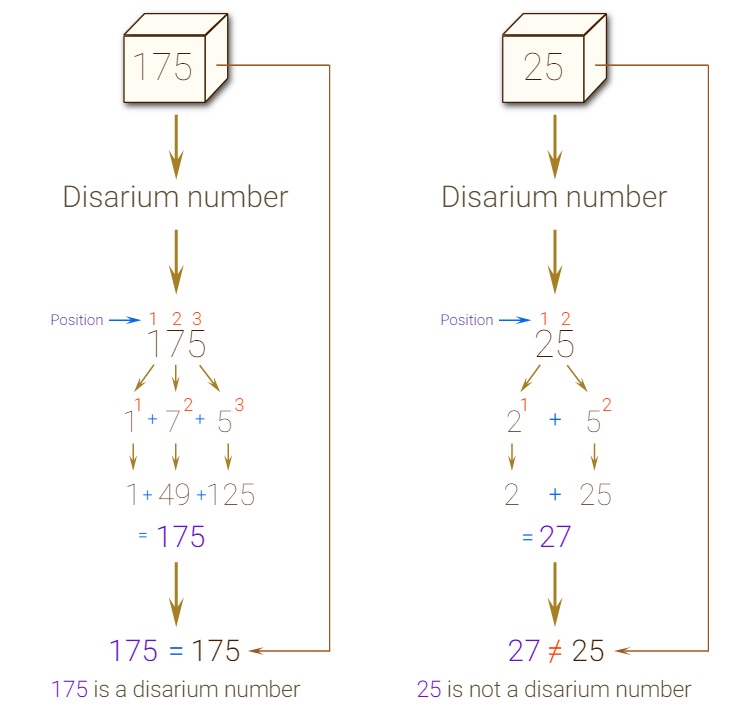
A number is be called Disarium if the sum of its digits powered with their respective position is equal with the number itself.
For example, 175 is a Disarium number:
As 11 + 72 + 53 = 175
Some other DISARIUM are 89, 135, 175, 518 etc.
-----------------------------------------------------------------------------------------------------------------------------¶
In this program, we need to print all the disarium numbers between 1 and 100 by following the algorithm as given below:
ALGORITHM:¶
STEP 1:
calculate_length() counts the digits present in a number.
Use a while loop to check whether the number variable is equal to 0 or not.
Divide the number variable by 10 and increment the length variable by 1.
Return length.
STEP 2:
sum_of_digits() calculates the sum of digits raised to their respective positions.
Make a call to calculate_length() to get the number of digits present in a given number and store the value in length variable.
Using the while loop calculate the remainder variable repeatedly by dividing the number with 10.
Calculate the value of result variable by adding the result variable to the remainder variable raised to power its length position.
STEP 3:
To display all the Disarium numbers between 1 and 100.
Start a loop from 1 to 100, then make a call to sum_of_digits() method for each value from 1 to 100 and store the return value into the result variable.
`
- If the value of the result is equal to the number, it implies that the given number is a Disarium number. Hence, display it.
-----------------------------------------------------------------------------------------------------------------------------¶
-----------------------------------------------------------------------------------------------------------------------------¶
In cryptography, Caesar cipher is one of the simplest and most widely known encryption techniques. It is also known with other names like Caesar's cipher, the shift cipher, Caesar's code or Caesar shift. This encryption technique is used to encrypt plain text, so only the person you want can read it. The method is named after Julius Caesar, who used it in his private correspondence.
In this encryption technique, to encrypt our data, we have to replace each letter in the text by some other letter at a fixed difference. Let's say, there is a letter 'T' then with a right shift of 1 it will be 'U' and with a left shift of 1 it will become 'S'. So here, the difference is 1 and the direction will also be same for a text. Either we can use left shift or right, not both in same text.
Let's understand it with an easy example.
For example, suppose we have text "abcdef" to be encrypted. Then what we can do is replace each of letter present in the text by another letter having fixed difference. Lets say we want right shift by 3 then each letter of the above text have to replaced by the letter, positioned 3 steps from the letter.
Plaintext: abcdef
Ciphertext: defghi

Now user can't read this text until he/she have the decryption key. Decryption key is nothing just the knowledge about how we have shifted those letters while encrypting it. To decrypt this we have to left shift all the letters by 3.
That was the basic concept of Caesar cipher. If we see this encryption technique in mathematical way then the formula to get encrypted letter will be:
c = (x + n) mod 26
where, c is the place value of encrypted letter, x is the place value of actual letter and n is the number that shows us how many positions of letters we have to replace.
On other hand, to decrypt each letter we'll use the formula given below:
c = (x – n) mod 26
-----------------------------------------------------------------------------------------------------------------------------¶
# Code to generate Disarium number starts
def calculate_length(number):
length = 0
while number != 0:
length = length + 1
number = number // 10
return length
# sum_of_digits() will calculates the sum of digits powered with their respective position
def sum_of_digits(number):
remainder = result = 0
length = calculate_length(number)
while number > 0:
remainder = number % 10
result = result + (remainder ** length)
number = number // 10
length = length - 1
return result
def print_disarium():
result = 0
# Displays all Disarium numbers between 1 and 100
print("Disarium numbers between 1 and 100 are \n")
for each_number in range(1, 101):
result = sum_of_digits(each_number)
if result == each_number:
print(each_number)
# Code to generate Disarium number ends
# # Code for Caesar Cipher technique starts
def encrypt_text(input_text, shift_pattern):
cipher_result = ""
# Traverse the plain text
for each_char in input_text:
# Check for empty spaces
if each_char == " ":
cipher_result = cipher_result + each_char
elif each_char.isupper():
# Encrypt the uppercase characters in plain text
cipher_result = cipher_result + chr(
(ord(each_char) + shift_pattern - 65) % 26 + 65
)
else:
# Encrypt the lowercase characters in plain text
cipher_result = cipher_result + chr(
(ord(each_char) + shift_pattern - 97) % 26 + 97
)
return cipher_result
# # Code to apply Caesar Cipher technique end
def user_input():
while True:
print("Enter 1 to Print all the Disarium number between 1 and 100 \n")
print("Enter 2 to Encrypt the text using Caesar Cipher technique \n")
print("Enter 3 to Exit the program \n")
choice = int(input())
print("")
if choice == 1:
print_disarium()
elif choice == 2:
input_text = input("Enter a text: \n")
shift_pattern = int(input("Enter Shift Pattern for encryption: \n"))
encrypted_text = encrypt_text(input_text, shift_pattern)
print(f"The encrypted text is {encrypted_text} \n")
else:
break
if __name__ == "__main__":
user_input()
Enter 1 to Print all the Disarium number between 1 and 100 Enter 2 to Encrypt the text using Caesar Cipher technique Enter 3 to Exit the program 1 Disarium numbers between 1 and 100 are 1 2 3 4 5 6 7 8 9 89 Enter 1 to Print all the Disarium number between 1 and 100 Enter 2 to Encrypt the text using Caesar Cipher technique Enter 3 to Exit the program 2 Enter a text: abcdef Enter Shift Pattern for encryption: 3 The encrypted text is defghi Enter 1 to Print all the Disarium number between 1 and 100 Enter 2 to Encrypt the text using Caesar Cipher technique Enter 3 to Exit the program 3