Model Checking¶
After running an MCMC simulation, sample returns an arviz.InferenceData object containing the samples for all the stochastic and named deterministic random variables. The final step in Bayesian computation is model checking, in order to ensure that inferences derived from your sample are valid. There are two components to model checking:
- Convergence diagnostics
- Goodness of fit
Convergence diagnostics are intended to detect lack of convergence in the Markov chain Monte Carlo sample; it is used to ensure that you have not halted your sampling too early. However, a converged model is not guaranteed to be a good model. The second component of model checking, goodness of fit, is used to check the internal validity of the model, by comparing predictions from the model to the data used to fit the model.
Convergence Diagnostics¶
Valid inferences from sequences of MCMC samples are based on the assumption that the samples are derived from the true posterior distribution of interest. Theory guarantees this condition as the number of iterations approaches infinity. It is important, therefore, to determine the minimum number of samples required to ensure a reasonable approximation to the target posterior density. Unfortunately, no universal threshold exists across all problems, so convergence must be assessed independently each time MCMC estimation is performed. The procedures for verifying convergence are collectively known as convergence diagnostics.
One approach to analyzing convergence is analytical, whereby the variance of the sample at different sections of the chain are compared to that of the limiting distribution. These methods use distance metrics to analyze convergence, or place theoretical bounds on the sample variance, and though they are promising, they are generally difficult to use and are not prominent in the MCMC literature. More common is a statistical approach to assessing convergence. With this approach, rather than considering the properties of the theoretical target distribution, only the statistical properties of the observed chain are analyzed. Reliance on the sample alone restricts such convergence criteria to heuristics. As a result, convergence cannot be guaranteed. Although evidence for lack of convergence using statistical convergence diagnostics will correctly imply lack of convergence in the chain, the absence of such evidence will not guarantee convergence in the chain. Nevertheless, negative results for one or more criteria may provide some measure of assurance to users that their sample will provide valid inferences.
For most simple models, convergence will occur quickly, sometimes within a the first several hundred iterations, after which all remaining samples of the chain may be used to calculate posterior quantities. For more complex models, convergence requires a significantly longer burn-in period; sometimes orders of magnitude more samples are needed. Frequently, lack of convergence will be caused by poor mixing. Recall that mixing refers to the degree to which the Markov chain explores the support of the posterior distribution. Poor mixing may stem from inappropriate proposals (if one is using the Metropolis-Hastings sampler) or from attempting to estimate models with highly correlated variables.
Example: Effect of coaching on SAT scores¶
This example was taken from Gelman et al. (2013):
A study was performed for the Educational Testing Service to analyze the effects of special coaching programs on test scores. Separate randomized experiments were performed to estimate the effects of coaching programs for the SAT-V (Scholastic Aptitude Test- Verbal) in each of eight high schools. The outcome variable in each study was the score on a special administration of the SAT-V, a standardized multiple choice test administered by the Educational Testing Service and used to help colleges make admissions decisions; the scores can vary between 200 and 800, with mean about 500 and standard deviation about 100. The SAT examinations are designed to be resistant to short-term efforts directed specifically toward improving performance on the test; instead they are designed to reflect knowledge acquired and abilities developed over many years of education. Nevertheless, each of the eight schools in this study considered its short-term coaching program to be successful at increasing SAT scores. Also, there was no prior reason to believe that any of the eight programs was more effective than any other or that some were more similar in effect to each other than to any other.
We are given the estimated coaching effects (y) and their sampling variances (s). The estimates were obtained by independent experiments, with relatively large sample sizes (over thirty students in each school), so you it can be assumed that they have approximately normal sampling distributions with known variances variances.
%matplotlib inline
import numpy as np
import pymc as pm
import arviz as az
import seaborn as sns; sns.set_context('notebook')
import warnings
warnings.filterwarnings("ignore", module="mkl_fft")
warnings.filterwarnings("ignore", module="matplotlib")
y = np.array([28, 8, -3, 7, -1, 1, 18, 12])
s = np.array([15, 10, 16, 11, 9, 11, 10, 18])
J = len(y)
with pm.Model() as schools:
eta = pm.Normal("eta", 0, 1, shape=J)
mu = pm.Normal("mu", 0, sigma=1e6)
tau = pm.HalfCauchy("tau", 5)
theta = mu + tau * eta
obs = pm.Normal("obs", theta, sigma=s, observed=y)
with schools:
schools_trace = pm.sample(1000, tune=2000, target_accept=0.9)
az.plot_trace(schools_trace, var_names=['mu', 'tau']);
Informal Methods¶
The most straightforward approach for assessing convergence is based on simply plotting and inspecting traces and histograms of the observed MCMC sample, as was done in the cell above. If the trace of values for each of the stochastics exhibits asymptotic behavior over the last $m$ iterations, this may be satisfactory evidence for convergence.
A similar approach involves plotting a histogram for every set of $k$ iterations (perhaps 50-100) beyond some burn in threshold $n$; if the histograms are not visibly different among the sample intervals, this may be considered some evidence for convergence. Note that such diagnostics should be carried out for each stochastic estimated by the MCMC algorithm, because convergent behavior by one variable does not imply evidence for convergence for other variables in the analysis.
import matplotlib.pyplot as plt
beta_trace = schools_trace.posterior['mu'].stack(sample=("chain", "draw"))
fig, axes = plt.subplots(2, 5, figsize=(14,6))
axes = axes.ravel()
for i in range(10):
axes[i].hist(beta_trace[100*i:100*(i+1)])
plt.tight_layout()
An extension of this approach can be taken when multiple parallel chains are run, rather than just a single, long chain. In this case, the final values of $c$ chains run for $n$ iterations are plotted in a histogram; just as above, this is repeated every $k$ iterations thereafter, and the histograms of the endpoints are plotted again and compared to the previous histogram. This is repeated until consecutive histograms are indistinguishable.
Another ad hoc method for detecting lack of convergence is to examine the traces of several MCMC chains initialized with different starting values. Overlaying these traces on the same set of axes should (if convergence has occurred) show each chain tending toward the same equilibrium value, with approximately the same variance. Recall that the tendency for some Markov chains to converge to the true (unknown) value from diverse initial values is called ergodicity. This property is guaranteed by the reversible chains constructed using MCMC, and should be observable using this technique. Again, however, this approach is only a heuristic method, and cannot always detect lack of convergence, even though chains may appear ergodic.
with schools:
tr = pm.sample(200, tune=0, cores=2, initvals=[{'mu': -10.}, {'mu': 10.}], step=pm.Metropolis(),
discard_tuned_samples=False, random_seed=42)
colors = 'rbkgcy'
for c in tr.sample_stats.chain:
plt.plot(tr.posterior.sel(chain=c).mu, f'{colors[int(c)]}--')
A principal reason that evidence from informal techniques cannot guarantee convergence is a phenomenon called *metastability*. Chains may appear to have converged to the true equilibrium value, displaying excellent qualities by any of the methods described above. However, after some period of stability around this value, the chain may suddenly move to another region of the parameter space. This period of metastability can sometimes be very long, and therefore escape detection by these convergence diagnostics. Unfortunately, there is no statistical technique available for detecting metastability.
Formal Methods¶
Along with the ad hoc techniques described above, a few more formal methods exist which are prevalent in the literature. These are considered more formal because they are based on existing statistical methods, such as time series analysis.
$\hat{R}$ Diagnostic¶
A second convergence diagnostic provided by PyMC is the Gelman-Rubin statistic Gelman and Rubin (1992), referred to as R-hat. This diagnostic uses multiple chains to check for lack of convergence, and is based on the notion that if multiple chains have converged, by definition they should appear very similar to one another; if not, one or more of the chains has failed to converge.
The Gelman-Rubin diagnostic uses an analysis of variance approach to assessing convergence. That is, it calculates both the between-chain varaince (B) and within-chain varaince (W), and assesses whether they are different enough to worry about convergence. Assuming $m$ chains, each of length $n$, quantities are calculated by:
$$\begin{align}B &= \frac{n}{m-1} \sum_{j=1}^m (\bar{\theta}_{.j} - \bar{\theta}_{..})^2 \\ W &= \frac{1}{m} \sum_{j=1}^m \left[ \frac{1}{n-1} \sum_{i=1}^n (\theta_{ij} - \bar{\theta}_{.j})^2 \right] \end{align}$$for each scalar estimand $\theta$. Using these values, an estimate of the marginal posterior variance of $\theta$ can be calculated:
$$\hat{\text{Var}}(\theta | y) = \frac{n-1}{n} W + \frac{1}{n} B$$Assuming $\theta$ was initialized to arbitrary starting points in each chain, this quantity will overestimate the true marginal posterior variance. At the same time, $W$ will tend to underestimate the within-chain variance early in the sampling run. However, in the limit as $n \rightarrow \infty$, both quantities will converge to the true variance of $\theta$. In light of this, the Gelman-Rubin statistic monitors convergence using the ratio:
$$\hat{R} = \sqrt{\frac{\hat{\text{Var}}(\theta | y)}{W}}$$This is called the potential scale reduction, since it is an estimate of the potential reduction in the scale of $\theta$ as the number of simulations tends to infinity. In practice, we look for values of $\hat{R}$ close to one (say, less than 1.1) to be confident that a particular estimand has converged.
In ArviZ, the function
rhat will calculate $\hat{R}$ for each stochastic node in
the passed model. Specifically, it calulates split-$\hat{R}$, which compares the first half to the second half of each chain, to allow for within-chain detection of lack of convergence.
az.rhat(schools_trace)
When calling the arviz.plot_forest function, the $\hat{R}$ values will be plotted alongside the
posterior intervals when the r_hat argument is set to True.
az.plot_forest(schools_trace, var_names=['eta'], r_hat=True, combined=True);
Autocorrelation¶
In general, samples drawn from MCMC algorithms will be autocorrelated. This is not a big deal, other than the fact that autocorrelated chains may require longer sampling in order to adequately characterize posterior quantities of interest. The calculation of autocorrelation is performed for each lag $i=1,2,\ldots,k$ (the correlation at lag 0 is, of course, 1) by:
$$\hat{\rho}_i = 1 - \frac{V_i}{2\hat{\text{Var}}(\theta | y)}$$where $\hat{\text{Var}}(\theta | y)$ is the same estimated variance as calculated for the Gelman-Rubin statistic, and $V_i$ is the variogram at lag $i$ for $\theta$:
$$\text{V}_i = \frac{1}{m(n-i)}\sum_{j=1}^m \sum_{k=i+1}^n (\theta_{jk} - \theta_{j(k-i)})^2$$This autocorrelation can be visualized using the plot_autocorr function in ArviZ:
az.plot_autocorr(tr, var_names=['mu']);
Effective sample size¶
The effective sample size is estimated using the partial sum:
$$\hat{n}_{eff} = \frac{mn}{1 + 2\sum_{i=1}^T \hat{\rho}_i}$$where $T$ is the first odd integer such that $\hat{\rho}_{T+1} + \hat{\rho}_{T+2}$ is negative.
The issue here is related to the fact that we are estimating the effective sample size from the fit output. Values of $n_{eff} / n_{iter} < 0.001$ indicate a biased estimator, resulting in an overestimate of the true effective sample size.
az.summary(schools_trace)
Both low $n_{eff}$ and high $\hat{R}$ indicate poor mixing.
It is tempting to want to thin the chain to eliminate the autocorrelation (e.g. taking every 20th sample from the traces above), but this is a waste of time. Since thinning deliberately throws out the majority of the samples, no efficiency is gained; you ultimately require more samples to achive a particular desired sample size.
ESS can also be added to forest plots by setting ess=True.
az.plot_forest(schools_trace, var_names=['eta'], r_hat=True, ess=True, combined=True);
Diagnostics for Gradient-based Samplers¶
Hamiltonian Monte Carlo is a powerful and efficient MCMC sampler when set up appropriately. However, this typically requires careful tuning of the sampler parameters, such as tree depth, leapfrog step size and target acceptance rate. Fortunately, the NUTS algorithm takes care of some of this for us. Nevertheless, tuning must be carefully monitored for failures that frequently arise. This is particularly the case when fitting challenging models, such as those with high curvature or heavy tails.
Details of NUTS Sampling¶
NUTS uses a recursive algorithm to build a set of likely candidate points that spans a wide swath of the target distribution. True to its name, it stops automatically when it starts to double back and retrace its steps.
The algorithm employs binary doubling, which takes leapfrog steps alternating in direction with respect to the initial gradient. That is, one step is taken in the forward direction, two in the reverse direction, then four, eight, etc. The result is a balanced, binary tree with nodes comprised of Hamiltonian states.
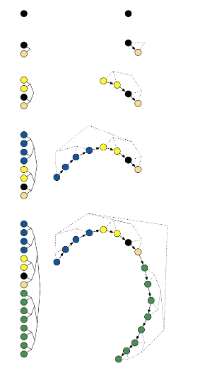
Doubling process builds a balanced binary tree whose leaf nodes correspond to position-momentum states. Doubling is halted when the subtrajectory from the leftmost to the rightmost nodes of any balanced subtree of the overall binary tree starts to double back on itself

To ensure detailed balance, a slice variable is sampled from:
$$ u \sim \text{Uniform}(0, \exp[L(\theta) - 0.5 r \cdot r])$$where $r$ is the initial momentum vector. The next sample is then chosen uniformly from the points in the remaining balanced tree.
Diagnosing Pathologies in PyMC¶
Fortunately, however, gradient-based sampling provides the ability to diagnose these pathologies. PyMC makes several diagnostic statistics available as attributes of the InferenceData.sample_stats output dataset.
schools_trace.sample_stats
process_time_diff: The time it took to draw the sample, as defined by the python standard library time.process_time. This counts all the CPU time, including worker processes in BLAS and OpenMP.step_size: The current integration step size.diverging: (boolean) Indicates the presence of leapfrog transitions with large energy deviation from starting and subsequent termination of the trajectory. “large” is defined as max_energy_error going over a threshold.lp: The joint log posterior density for the model (up to an additive constant).energy: The value of the Hamiltonian energy for the accepted proposal (up to an additive constant).energy_error: The difference in the Hamiltonian energy between the initial point and the accepted proposal.perf_counter_diff: The time it took to draw the sample, as defined by the python standard library time.perf_counter (wall time).perf_counter_start: The value of time.perf_counter at the beginning of the computation of the draw.n_steps: The number of leapfrog steps computed. It is related to tree_depth with n_steps <= 2^tree_dept.max_energy_error: The maximum absolute difference in Hamiltonian energy between the initial point and all possible samples in the proposed tree.acceptance_rate: The average acceptance probabilities of all possible samples in the proposed tree.step_size_bar: The current best known step-size. After the tuning samples, the step size is set to this value. This should converge during tuning.tree_depth: The number of tree doublings in the balanced binary tree.
If the name of the statistic does not clash with the name of one of the variables, we can use indexing to get the values. The values for the chains will be concatenated.
with schools:
trace = pm.sample(1000, tune=2000, init=None, cores=2, discard_tuned_samples=False)
The failure of HMC samplers to be geometrically ergodic with respect to any target distribution manifests itself in distinct behaviors. One of these behaviors is the appearance of divergences that indicate the Hamiltonian Markov chain has encountered regions of high curvature in the target distribution which it cannot adequately explore.
The NUTS step method has a maximum tree depth parameter so that infinite loops (which can occur for non-identified models) are avoided. When the maximum tree depth is reached (the default value is 10), the trajectory is stopped. However complex (but identifiable) models can saturate this threshold, which reduces sampling efficiency.
The InferenceData object stores the tree depth for each iteration, so inspecting these traces can reveal saturation if it is occurring.
trace.sample_stats["tree_depth"].plot(col="chain", ls="none", marker=".", alpha=0.3);
We can also check the acceptance for the trees that generated this sample. The mean of these values across all samples (except the tuning stage) is expected to be the same as target_accept, which is 0.8 by default.
az.plot_posterior(
trace, group="sample_stats", var_names="acceptance_rate", hdi_prob="hide", kind="hist"
);
Divergent transitions¶
Recall that simulating Hamiltonian dynamics via a symplectic integrator uses a discrete approximation of a continuous function. This is only a reasonable approximation when the step sizes of the integrator are suitably small. A divergent transition may indicate that the approximation is poor.
If there are too many divergent transitions, then samples are not being drawn from the full posterior, and inferences based on the resulting sample will be biased
If there are diverging transitions, PyMC will issue warnings indicating how many were discovered. We can obtain the indices of them from the trace.
trace.sample_stats["diverging"].sum()
If the location of the divergences are distributed differently than the samples as a whole, this is an indication that the posterior is not being well explored.
az.plot_trace(trace, var_names=['mu']);
az.plot_parallel(trace, norm_method="normal");
Exercise: Eight schools centered parameterization¶
Implement the eight schools example using the centered parameterization of the mean, and inspect the traces for divergences.
# Write your answer here
Bayesian Fraction of Missing Information¶
The Bayesian fraction of missing information (BFMI) is a measure of how hard it is to sample level sets of the posterior at each iteration. Specifically, it quantifies how well momentum resampling matches the marginal energy distribution.
$$\text{BFMI} = \frac{\mathbb{E}_{\pi}[\text{Var}_{\pi_{E|q}}(E|q)]}{\text{Var}_{\pi_{E}}(E)}$$$$\widehat{\text{BFMI}} = \frac{\sum_{i=1}^N (E_n - E_{n-1})^2}{\sum_{i=1}^N (E_n - \bar{E})^2}$$A small value indicates that the adaptation phase of the sampler was unsuccessful, and invoking the central limit theorem may not be valid. It indicates whether the sampler is able to efficiently explore the posterior distribution.
Though there is not an established rule of thumb for an adequate threshold, values close to one are optimal. Reparameterizing the model is sometimes helpful for improving this statistic.
az.bfmi(trace)
Another way of diagnosting this phenomenon is by comparing the overall distribution of energy levels with the change of energy between successive samples. Ideally, they should be very similar.
If the distribution of energy transitions is narrow relative to the marginal energy distribution, this is a sign of inefficient sampling, as many transitions are required to completely explore the posterior. On the other hand, if the energy transition distribution is similar to that of the marginal energy, this is evidence of efficient sampling, resulting in near-independent samples from the posterior.
These quantities can be readily plotted, using the energy values in the model trace:
energy = trace.sample_stats['energy'].values.ravel()
energy_diff = np.diff(energy)
sns.kdeplot(energy - energy.mean(), label='energy')
sns.kdeplot(energy_diff, label='energy diff')
plt.legend();
Better yet, ArviZ includes a plot_energy function to automate this.
az.plot_energy(trace);
If the overall distribution of energy levels has longer tails, the efficiency of the sampler will deteriorate quickly.
Goodness of Fit¶
Checking for model convergence is only the first step in the evaluation of MCMC model outputs. It is possible for an entirely unsuitable model to converge, so additional steps are needed to ensure that the estimated model adequately fits the data. One intuitive way of evaluating model fit is to compare model predictions with the observations used to fit the model. In other words, the fitted model can be used to simulate data, and the distribution of the simulated data should resemble the distribution of the actual data.
Fortunately, simulating data from the model is a natural component of the Bayesian modelling framework. Recall, from the discussion on imputation of missing data, the posterior predictive distribution:
$$p(\tilde{y}|y) = \int p(\tilde{y}|\theta) f(\theta|y) d\theta$$Here, $\tilde{y}$ represents some hypothetical new data that would be expected, taking into account the posterior uncertainty in the model parameters.
Sampling from the posterior predictive distribution is easy
in PyMC. The sample_ppc function draws posterior predictive checks from all of the data likelhioods.
The posterior predictive distribution of deaths uses the same functional form as the data likelihood, in this case a binomial stochastic. Here is the corresponding sample from the posterior predictive distribution (we typically need very few samples relative to the MCMC sample):
with schools:
scores_sim = pm.sample_posterior_predictive(schools_trace)
schools_trace.extend(scores_sim)
The degree to which simulated data correspond to observations can be evaluated in at least two ways. First, these quantities can simply be compared visually. This allows for a qualitative comparison of model-based replicates and observations. If there is poor fit, the true value of the data may appear in the tails of the histogram of replicated data, while a good fit will tend to show the true data in high-probability regions of the posterior predictive distribution. The Matplot package in PyMC provides an easy way of producing such plots, via the gof_plot function.
az.plot_ppc(schools_trace);
Leave One Out (LOO) Probability Integral Transform (PIT)¶
Another flavor of goodness-of-fit checking involves marginal posterior predictive checks. In this approach, we compare individual observations with their corresponding posterior predictive samples. The methodology combines two techniques: Leave-one-out (LOO) cross-validation and the probability integral transform (PIT).
Cross-validation divides a given dataset into K subsets, where K-1 subsets are used to fit the model and the excluded subset is used to validate. This process is performed times, where each subset is given the opportunity to be held out. LOO is one extreme of this general procedure, where the number of subsets is equal to the number of observations so that each iteration only one observation is excluded.
For a given random variable $X$, the cumulative density function is:
$$Y = F_x(X) = Pr(x \le X)$$ We can use a sample $x = (x_1, \ldots, x_n)$ to estimate $F_x$, and this will be approximately uniform distributed, particularly as $n$ gets large. This is the probability integral transform, and it is used by the LOO-PIT diagnostic to on each LOO model fit. That is, for each obervation, we calculate:
$$ P\left(y_{i}<y^{*} \mid y_{-i}\right)=\int_{-\infty}^{y_{i}} p\left(y^{*} \mid y_{-i}\right) d y^{*} $$We can graphically compare the kernel density estimate of the LOO-PIT values and compare them to corresponding draws from a uniform random variable. This is implemented in plot_loo_pit:
az.plot_loo_pit(schools_trace, y='obs');
An alternative visualiztion of this involves using the empirical CDF. Passing ecdf=True to plot_loo_pit will generate a plot of the difference between the LOO-PIT ECDF and the uniform CDF. For a perfect fit, this difference will be zero, but we are looking for values to fall within some credible interval for each observed value.
az.plot_loo_pit(schools_trace, y='obs', ecdf=True);
Example: Stomach Cancer¶
Tsutakawa et al. (1985) provides mortality data for stomach cancer among men aged 45-64 in several cities in Missouri. The file cancer.csv contains deaths $y_i$ and subjects at risk $n_i$ for 20 cities from this dataset.
Fit a simple binomial model of cancer mortality rate, and evaluate model fit. If the fit is poor, try to reparameterize the model to improve the fit.
import pandas as pd
DATA_URL = 'https://raw.githubusercontent.com/fonnesbeck/Bios8366/master/data/'
try:
cancer = pd.read_csv('../data/cancer.csv')
except FileNotFoundError:
cancer = pd.read_csv(DATA_URL + 'cancer.csv')
# Write your answer here
References¶
Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science. A Review Journal of the Institute of Mathematical Statistics, 457–472.
Abril, O. (2019). LOO-PIT Tutorial
Betancourt, M. (2017). A Conceptual Introduction to Hamiltonian Monte Carlo. arXiv.org.
Gelman, Andrew, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. 2013. Bayesian Data Analysis, Third Edition. CRC Press.