!pip install jax jaxlib
Hamiltonian Monte Carlo¶
Having introduced first-generation MCMC methods previously, we will now turn our attention to a more sophisticated class of algorithm, which improve upon random-walk jump algorithms by using information about the posterior distribution to inform candidate transitions: namely, gradient information.
In order to implement these methods in code, we require more powerful mathematical software tools that allow for automated gradient calculation. There are several open source toolboxes that can support gradient-based Monte Carlo methods, and we will look at one of them in detail.
Introduction to Mathematical Expressions with Aesara¶
Aesara is a Python library that allows you to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Aesara features:
- efficient symbolic differentiation – Aesara does your derivatives for function with one or many inputs.
- speed and stability optimizations – Get the right answer for log(1+x) even when x is really tiny.
- evaluate expressions faster - Implements an extensible graph transpilation framework that currently provides compilation via C, JAX, and Numba
- extensive unit-testing and self-verification – Detect and diagnose errors.
- hackable, pure-Python codebase - Extensible graph framework suitable for rapid development of custom operators and symbolic optimizations
Aesara is based on one of the most widely-used Python tensor libraries: Theano
After a brief introduction to the Aesara package, we will use it to implement a modern MCMC algorithm, Hamiltonian Monte Carlo (HMC).
import aesara.tensor as at
x = at.scalar(name='x')
y = at.scalar(name='y')
The Aesara symbols we have created are TensorVariable objects
type(x)
By default, the data type is float64.
x.type
A tensor is a generalization of an array to (potentially) multiple dimensions. Thus, everything from a scalar to a multi-dimensional hyper-matrix can be accomodated with the same abstraction. All expressions defined in Aesara are performed by associating tensors with operations and with one another.
Step 2 - Symbolic Expressions¶
The second step is to combine x and y into their sum z:
z = x + y
z is yet another Variable which represents the addition of
x and y. You can use the pp function to pretty-print out the computation associated to z.
from aesara.printing import pp
print(pp(z))
Variables can have attributes, such as a meaningful name.
z.name = 'x plus y'
So, we have created an expression for the addition of x and y and called it z.
Step 3 - Compiling a Function¶
The last step is to create a function taking x and y as inputs and giving z as output:
from aesara import function
f = function(inputs=[x, y], outputs=z, mode='NUMBA')
The first argument to function() is a list of Variables that will be provided as inputs to the function. The second argument is a single Variable or a list of Variables. For either case, the second argument is what we want to see as output when we apply the function. f may then be used like a normal Python function.
By default, Aesara functions are compiled to C, but this can be replaced by other backend options with the mode argument, which currently accepts 'NUMBA' or 'JAX' as alternatives (assuming they are installed on your system).
Let's have a look at the graph of our function:
from aesara import dprint
dprint(f)
Now we can call the function:
print(f(2, 3))
print(f(16.3, 12.1))
If you are following along and typing into an interpreter, you may have
noticed that there was a slight delay in executing the function
instruction. Behind the scenes, f was being compiled into C code (or Numba, or Jax).
Internally, Aesara builds a graph structure composed of interconnected Variable nodes, op nodes and apply nodes.
An op node encapsulates a particular mathematical operation, such as an arithmetic operation or a transformation.
An apply node represents the application of an op to some variables. It is important to draw the difference between the definition of a computation represented by an op and its application to some actual data which is represented by the apply node.
A Variable is the main data structure you work with when
using Aesara. By calling at.scalar with a string argument, you create a
Variable representing a floating-point scalar quantity with the
given name. If you provide no argument, the symbol will be unnamed. Names
are not required, but they can help debugging.
Adding Two Matrices¶
If we want to work with matrices instead of scalars, the only change from the previous example is that you need to instantiate x and y using the matrix Types:
x = at.dmatrix('x')
y = at.dmatrix('y')
z = x + y
f = function([x, y], z, mode='JAX')
Here is the expression graph corresponding to the addition of x and y:
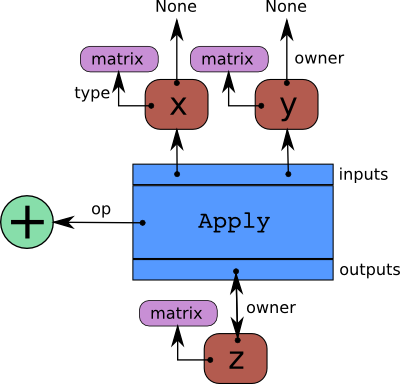
matrix is the Type for matrices of doubles. Then we can use
our new function on 2D arrays:
f([[1, 2], [3, 4]], [[10, 20], [30, 40]])
Each node in the expression graph is aware of its parent nodes.
z.owner
The following types are available:
- byte:
bscalar, bvector, bmatrix, brow, bcol, btensor3, btensor4 - 16-bit integers:
wscalar, wvector, wmatrix, wrow, wcol, wtensor3, wtensor4 - 32-bit integers:
iscalar, ivector, imatrix, irow, icol, itensor3, itensor4 - 64-bit integers:
lscalar, lvector, lmatrix, lrow, lcol, ltensor3, ltensor4 - float:
fscalar, fvector, fmatrix, frow, fcol, ftensor3, ftensor4 - double:
dscalar, dvector, dmatrix, drow, dcol, dtensor3, dtensor4 - complex:
cscalar, cvector, cmatrix, crow, ccol, ctensor3, ctensor4
An example of a slightly more interesting function is the logistic curve. Let's start with a matrix variable:
x = at.matrix('x')
and apply the logistic transformation:
s = 1 / (1 + at.exp(-x))
s.name = 'logit-x'
Again, this is just an op node which acts as a placeholder for the operation; we still need to define the apply node, as a function:
logistic = function([x], s)
print(logistic([[0, 1], [-1, -2]]))
Aesara supports functions with multiple outputs. For example, we can compute the elementwise difference, absolute difference, and squared difference between two matrices a and b at the same time.
a, b = at.matrices('a', 'b')
diff = a - b
abs_diff = abs(diff)
diff_squared = diff ** 2
When we use the function f, it returns the three computed results as a list.
f = function([a, b], [diff, abs_diff, diff_squared])
f([[1, 1], [1, 1]], [[0, 1], [2, 3]])
Manipulating the Graph¶
After an expression graph has been created, it can be modified as needed.
import aesara
list(aesara.graph.graph_inputs([z]))
For example, let's add a log transformation to z at the end of the graph:
w = at.log(z)
w.name = 'log of z'
dprint(w)
Let's now arbitrarily add an exponential transformation before the logarithm, essentially cancelling it out. This involves swapping out the parent node of w, which is currently x + y, with exp(x + y) using the clone_replace function:
parent_of_w = w.owner.inputs[0]
new_parent_of_w = at.exp(parent_of_w)
new_parent_of_w.name = 'exp(x + y)'
new_w = aesara.clone_replace(output=[w], replace={parent_of_w: new_parent_of_w})[0]
new_w.name = "log(exp(x + y))"
dprint(new_w)
Setting a Default Value for an Argument¶
Let's say you want to define a function that adds two numbers, except that if you only provide one number, the other input is assumed to be one. In Python, the default value for parameters (keywork argument) achieves this effect.
In Aesara we make use of the In class, which allows you to specify properties of your function's parameters with greater detail. Here we give a default value of 1 for y by creating an In instance with its value field set to 1. Inputs with default values must follow inputs without default values (like Python's functions). There can be multiple inputs with default values. These parameters can be set positionally or by name, as in standard Python.
from aesara import In
x, y, w = at.dscalars('x', 'y', 'w')
z = (x + y) * w
g = function([x, In(y, value=1), In(w, value=2, name='w_by_name')], z)
print(f'g(33) = {g(33)}')
print(f'g(33, 0, 1) = {g(33, 0, 1)}')
print(f'g(33, w_by_name=1) = {g(33, w_by_name=1)}')
Maintaining State with Shared Variables¶
It is also possible to make a function with an internal state. For example, let’s say we want to make an accumulator: at the beginning, the state is initialized to zero. Then, on each function call, the state is incremented by the function’s argument.
First let’s define the accumulator function. It adds its argument to the internal state, and returns the old state value.
from aesara import shared
state = shared(0)
inc = at.iscalar('inc')
accumulator = function([inc], state, updates=[(state, state+inc)])
This code introduces a few new concepts. The shared function constructs so-called shared variables.
state = shared(0)
These are hybrid symbolic and non-symbolic variables whose value may be shared between multiple functions. Shared variables can be used in symbolic expressions but they also have an internal value that defines the value taken by this symbolic variable in all the functions that use it. It is called a shared variable because its value is shared between many functions. The value can be accessed and modified by the get_value and set_value methods.
The other new thing in this code is the updates parameter of function.
updates=[(state, state+inc)
updates must be supplied with a list of pairs of the form (shared-variable, new expression). It can also be a dictionary whose keys are shared-variables and values are the new expressions. Here, the accumulator replaces the state‘s value with the sum of state and the increment amount inc.
print(state.get_value())
print(accumulator(1))
print(state.get_value())
print(accumulator(300))
print(state.get_value())
It is possible to reset the state. Just use the set_value method:
state.set_value(-1)
print(accumulator(3))
print(state.get_value())
As we mentioned above, you can define more than one function to use the same shared variable. These functions can all update the value.
dec = at.iscalar('dec')
decrementor = function([dec], state, updates=[(state, state-dec)])
print(decrementor(2))
print(state.get_value())
You might be wondering why the updates mechanism exists. You can always achieve a similar result by returning the new expressions, and working with them in NumPy as usual. While the updates mechanism can be a syntactic convenience, it is mainly there for efficiency. Updates to shared variables can sometimes be done more quickly using in-place algorithms (e.g. low-rank matrix updates). Also, Aesara has more control over where and how shared variables are allocated, which is one of the important elements of getting good performance on the GPU.
Exercise: Create and manipulate Aesara objects¶
To give you some practice with basic Aesara data structures and functions, try making the operations below work by implementing the functions that are needed.
import numpy as np
def make_vector():
"""
Create and return a new Aesara vector.
"""
pass
def make_matrix():
"""
Create and return a new Aesara matrix.
"""
pass
def elemwise_mul(a, b):
"""
a: An Aesara matrix
b: An Aesara matrix
Calcuate the elementwise product of a and b and return it
"""
pass
def matrix_vector_mul(a, b):
"""
a: An Aesara matrix
b: An Aesara vector
Calculate the matrix-vector product of a and b and return it
"""
pass
a = make_vector()
b = make_vector()
c = elemwise_mul(a, b)
d = make_matrix()
e = matrix_vector_mul(d, c)
f = function([a, b, d], e)
rng = np.random.RandomState([1, 2, 3])
a_value = rng.randn(5).astype(a.dtype)
b_value = rng.rand(5).astype(b.dtype)
c_value = a_value * b_value
d_value = rng.randn(5, 5).astype(d.dtype)
expected = np.dot(d_value, c_value)
actual = f(a_value, b_value, d_value)
assert np.allclose(actual, expected)
print("SUCCESS!")
Example: Logistic regression¶
Here is a non-trivial example, which uses Aesara to estimate the parameters of a logistic regression model using gradient information. We will use the bioassay example as a test case:
import numpy as np
rng = np.random
dose = np.array([-0.86, -0.3 , -0.05, 0.73])
deaths = np.array([0, 1, 3, 5])
training_steps = 1000
We first declare Aesara symbolic variables:
x = at.vector("x")
y = at.vector("y")
w = shared(1., name="w")
b = shared(0., name="b")
print("Initial model:", w.get_value(), b.get_value())
... then construct the expression graph:
# Probability that target = 1
p_1 = 1 / (1 + at.exp(-(x*w + b)))
# The prediction threshold
prediction = p_1 > 0.5
# Cross-entropy loss function
xent = -y * at.log(p_1) - (5-y) * at.log(1-p_1)
# The cost to minimize
cost = xent.mean()
# Compute the gradient of the cost
gw, gb = at.grad(cost, [w, b])
Compile Aesara functions:
step = shared(10., name='step')
train = function(
inputs=[x, y],
outputs=[prediction, xent],
updates=((w, w - step * gw), (b, b - step * gb), (step, step * 0.99)),
mode='JAX')
predict = function(inputs=[x], outputs=prediction, mode='JAX')
Train model:
for i in range(training_steps):
pred, err = train(dose, deaths)
w, b = w.get_value(), b.get_value()
print("Final model:", w, b)
%matplotlib inline
import matplotlib.pyplot as plt
logit = lambda x: 1. / (1 + np.exp(-x))
xvals = np.linspace(-1, 1)
plt.plot(xvals, logit(w*xvals + b))
plt.plot(dose, deaths/5., 'ro')
Exercises: Gradients and functions¶
Let's try using the Aesara automatic gradient system to compute derivatives.
def grad_sum(x, y, z):
"""
x: A aesara variable
y: A aesara variable
z: A aesara expression involving x and y
Returns dz / dx + dz / dy
"""
pass
x = at.scalar()
y = at.scalar()
z = x + y
s = grad_sum(x, y, z)
assert s.eval({x: 0, y: 0}) == 2
print("SUCCESS!")
Now try compiling and running a simple function:
def evaluate(x, y, expr, x_value, y_value):
"""
x: A aesara variable
y: A aesara variable
expr: A aesara expression involving x and y
x_value: A numpy value
y_value: A numpy value
Returns the value of expr when x_value is substituted for x
and y_value is substituted for y
"""
pass
x = at.iscalar()
y = at.iscalar()
z = x + y
assert evaluate(x, y, z, 1, 2) == 3
print("SUCCESS!")
Random Numbers¶
Because in Aesara you first express everything symbolically and afterwards compile this expression to get functions, using pseudo-random numbers is not as straightforward as it is in NumPy.
The way to think about putting randomness into Aesara’s computations is to put random variables in your graph. Aesara will allocate a NumPy RandomStream object (a random number generator) for each such variable, and draw from it as necessary. We will call this sort of sequence of random numbers a random stream. Random streams are at their core shared variables, so the observations on shared variables hold here as well.
from aesara.tensor.random.utils import RandomStream
from aesara import function
srng = RandomStream(seed=234)
rv_u = srng.uniform(0, 1, size=(2,2))
rv_n = srng.normal(0, 1, size=(2,2))
Here, rv_u is a random stream of 2x2 matrices of draws from a uniform distribution, while rv_n is a random stream of 2x2 matrices of draws from a normal distribution.
f = function([], rv_u)
Now that we have wrapped our random number stream in a function, we have a random number generator. Each time we call f(), it returns a pseudo-random number and the internal state of the stream is updated, so that the next call to f() will return a different value.
f()
f()
g = function([], rv_n, no_default_updates=True) #Not updating rv_n.rng
In the case of the normal example, if we add the argument no_default_updates=True to function, then the random number stream state is not affected by calling the returned function (i.e. the state is not updated). In this case, calling g() multiple times will return the same numbers.
g()
g()
Its important to note that a random variable is drawn at most once during any single function execution. So the function below is guaranteed to return a value that is zero (except for rounding error) despite the fact that the expression rv_u appears multiple times.
nearly_zeros = function([], rv_u - rv_u - rv_u + rv_u)
nearly_zeros()
Looping in Aesara¶
The scan function provides the ability to write loops in Aesara. We are not able to use Python for loops with Aesara because Aesara needs to be able to build and optimize the expression graph before compiling it into faster code, and be able to use symbolic differentiation for calculating gradients.
Simple loop with accumulation¶
Assume that, given $k$ you want to get $A^k$ using a loop. More precisely, if $A$ is a tensor you want to compute $A^k$ elementwise. The python code might look like:
result = 1
for i in range(k):
result = result * A
There are three things here that we need to handle: the initial value assigned to result, the accumulation of results in result, and the unchanging variable A. Unchanging variables are passed to scan as non_sequences. Initialization occurs in outputs_info, and the accumulation happens automatically.
The equivalent Aesara code would be:
from aesara import scan
k = at.iscalar("k")
A = at.vector("A")
# Symbolic description of the result
result, updates = scan(
fn=lambda prior_result, A: prior_result * A,
outputs_info=at.ones_like(A),
non_sequences=A,
n_steps=k
)
# We only care about A**k, but scan has provided us with A**1 through A**k.
# Discard the values that we don't care about. Scan is smart enough to
# notice this and not waste memory saving them.
final_result = result[-1]
# compiled function that returns A**k
power = function(inputs=[A,k], outputs=final_result, updates=updates)
print(power(range(10),2))
print(power(range(10),4))
Let us go through the example line by line. What we did is first to construct a function (using a lambda expression) that given prior_result and A returns prior_result * A. The order of parameters is fixed by scan: the output of the prior call to fn is the first parameter, followed by all non-sequences.
Next we initialize the output as a tensor with same shape and dtype as A, filled with ones. We give A to scan as a non sequence parameter and specify the number of steps k to iterate over our lambda expression.
Scan returns a tuple containing our result (result) and a dictionary of updates (empty in this case). Note that the result is not a matrix, but a 3D tensor containing the value of $A^k$ for each step. We want the last value (after k steps) so we compile a function to return just that. Note that there is an optimization, that at compile time will detect that you are using just the last value of the result and ensure that scan does not store all the intermediate values that are used. So do not worry if A and k are large.
In addition to looping a fixed number of times, scan can iterate over the leading dimension of tensors (similar to Python’s for x in a_list).
The tensor(s) to be looped over should be provided to scan using the sequences keyword argument.
Example: polynomial calculation¶
Here’s an example that builds a symbolic calculation of a polynomial from a list of its coefficients:
coefficients = at.vector("coefficients")
x = at.scalar("x")
# Generate the components of the polynomial
components, updates = scan(fn=lambda coefficient, power, val: coefficient * (val ** power),
outputs_info=None,
sequences=[coefficients, at.arange(1000)],
non_sequences=x)
# Sum them up
polynomial = components.sum()
# Compile a function
calculate_polynomial = function(inputs=[coefficients, x], outputs=polynomial)
# Test
test_coefficients = np.asarray([1, 0, 2], dtype=np.float32)
test_value = 3
print(calculate_polynomial(test_coefficients, test_value))
Hamiltonian Monte Carlo¶
While flexible and easy to implement, Metropolis-Hastings sampling is a random walk sampler that might not be statistically efficient for many models. Specifically, for models of high dimension, random walk jumping algorithms do not perform well. It is not enough to simply guess at the next sample location; we need to make each iteration a useful draw from the posterior whenever we can, in order to have an efficient sampler for bigger models.
Since Bayesian inference is all about calculating expectations over posteriors, what we seek is an algorithm that explores the area of the parameter space that contains most of the non-zero probability. This region is called the typical set.
What's a Typical Set?¶
The typical set is where most of the probability density (mass) lies in a particular volume associated with the distribution. As the dimension of a model increases, this set moves progressively further from the mode, and becomes more singular, as the result of concentration of measure.
The typical set is a product of both the density, which is highest at the mode, and volume (that we integrate over), which increasingly becomes larger away from the mode as dimensionality increases. In fact, at high dimensions, the region around the mode contributes almost nothing to the expectation. We need an algorithm that will find this narrow region and explore it efficiently.
In this context, and when sampling from continuous variables, Hamiltonian (or Hybrid) Monte Carlo (HMC) can prove to be a powerful tool. It avoids random walk behavior by simulating a physical system governed by Hamiltonian dynamics, potentially avoiding tricky conditional distributions in the process.
In HMC, model samples are obtained by simulating a physical system, where particles move about a high-dimensional landscape, subject to potential and kinetic energies. Adapting the notation from Neal (1993), particles are characterized by a position vector or state $s \in \mathcal{R}^D$ and velocity vector $\phi \in \mathcal{R}^D$. The combined state of a particle is denoted as $\chi=(s,\phi)$.
The joint canonical distribution of the position and velocity can be expressed as a product of the marginal position (which is of interest) and the conditional distribution of the velocity:
$$\pi(s, \phi) = \pi(\phi | s) \pi(s)$$This joint probability can also be written in terms of an invariant Hamiltonian function:
$$\pi(s, \phi) \propto \exp(-H(s,\phi))$$The Hamiltonian is then defined as the sum of potential energy $E(s)$ and kinetic energy $K(\phi)$, as follows:
$$\mathcal{H}(s,\phi) = E(s) + K(\phi) = E(s) + \frac{1}{2} \sum_i \phi_i^2$$Instead of sampling $p(s)$ directly, HMC operates by sampling from the canonical distribution.
$$p(s,\phi) = \frac{1}{Z} \exp(-\mathcal{H}(s,\phi))=p(s)p(\phi)$$If we choose a momentum that is independent of position, marginalizing over $\phi$ is trivial and recovers the original distribution of interest.
Note that the Hamiltonian $\mathcal{H}$ is independent of the parameterization of the model, and therefore, captures the geometry of the phase space distribution, including typical set.
Hamiltonian Dynamics
State $s$ and velocity $\phi$ are modified such that $\mathcal{H}(s,\phi)$ remains constant throughout the simulation. The differential equations are given by:
$$\begin{aligned}\frac{ds_i}{dt} &= \frac{\partial \mathcal{H}}{\partial \phi_i} = \phi_i \\ \frac{d\phi_i}{dt} &= - \frac{\partial \mathcal{H}}{\partial s_i} = - \frac{\partial E}{\partial s_i} \end{aligned}$$As shown in Neal (1993), the above transformation preserves volume and is reversible. The above dynamics can thus be used as transition operators of a Markov chain and will leave $p(s,\phi)$ invariant. That chain by itself is not ergodic however, since simulating the dynamics maintains a fixed Hamiltonian $\mathcal{H}(s,\phi)$. HMC thus alternates Hamiltonian dynamic steps, with Gibbs sampling of the velocity. Because $p(s)$ and $p(\phi)$ are independent, sampling $\phi_{new} \sim p(\phi|s)$ is trivial since $p(\phi|s)=p(\phi)$, where $p(\phi)$ is often taken to be the univariate Gaussian.
The Leap-Frog Algorithm
In practice, we cannot simulate Hamiltonian dynamics exactly because of the problem of time discretization. There are several ways one can do this. To maintain invariance of the Markov chain however, care must be taken to preserve the properties of volume conservation and time reversibility. The leap-frog algorithm maintains these properties and operates in 3 steps:
$$\begin{aligned} \phi_i(t + \epsilon/2) &= \phi_i(t) - \frac{\epsilon}{2} \frac{\partial{}}{\partial s_i} E(s(t)) \\ s_i(t + \epsilon) &= s_i(t) + \epsilon \phi_i(t + \epsilon/2) \\ \phi_i(t + \epsilon) &= \phi_i(t + \epsilon/2) - \frac{\epsilon}{2} \frac{\partial{}}{\partial s_i} E(s(t + \epsilon)) \end{aligned}$$We thus perform a half-step update of the velocity at time $t+\epsilon/2$, which is then used to compute $s(t + \epsilon)$ and $\phi(t + \epsilon)$.
Accept / Reject
In practice, using finite stepsizes $\epsilon$ will not preserve $\mathcal{H}(s,\phi)$ exactly and will introduce bias in the simulation. Also, rounding errors due to the use of floating point numbers means that the above transformation will not be perfectly reversible.
HMC cancels these effects exactly by adding a Metropolis accept/reject stage, after $n$ leapfrog steps. The new state $\chi' = (s',\phi')$ is accepted with probability $p_{acc}(\chi,\chi')$, defined as:
$$p_{acc}(\chi,\chi') = min \left( 1, \frac{\exp(-\mathcal{H}(s',\phi')}{\exp(-\mathcal{H}(s,\phi)} \right)$$HMC Algorithm
We obtain a new HMC sample as follows:
- sample a new velocity from a univariate Gaussian distribution
- perform $n$ leapfrog steps to obtain the new state $\chi'$
- perform accept/reject move of $\chi'$
Implementing HMC Using Aesara¶
In Aesara, update dictionaries and shared variables provide a natural way to implement a sampling algorithm. The current state of the sampler can be represented as a Aesara shared variable, with HMC updates being implemented by the updates list of a Aesara function.
We breakdown the HMC algorithm into the following sub-components:
simulate_dynamics: a symbolic Python function which, given an initial position and velocity, will performn_stepsleapfrog updates and return the symbolic variables for the proposed state $\chi'$.hmc_move: a symbolic Python function which given a starting position, generates $\chi$ by randomly sampling a velocity vector. It then callssimulate_dynamicsand determines whether the transition $\chi \rightarrow \chi'$ is to be accepted.hmc_updates: a Python function which, given the symbolic outputs ofhmc_move, generates the list of updates for a single iteration of HMC.HMC_sampler: a Python helper class which wraps everything together.
simulate_dynamics
To perform $n$ leapfrog steps, we first need to define a function over which the algorithm can iterate. Instead of implementing leap frog verbatim, notice that we can obtain $s(t + n \epsilon)$ and $\phi(t + n \epsilon)$ by performing an initial half-step update for $\phi$, followed by $n$ full-step updates for $s,\phi$ and one last half-step update for $\phi$. In loop form, this gives:
$$\begin{aligned}\phi_i(t + \epsilon/2) &= \phi_i(t) - \frac{\epsilon}{2} \frac{\partial{}}{\partial s_i} E(s(t)) \\ s_i(t + \epsilon) &= s_i(t) + \epsilon \phi_i(t + \epsilon/2) \\ \text{For } m \in [2,n]\text{, perform full updates: } \\ \qquad \phi_i(t + (m - 1/2)\epsilon) &= \phi_i(t + (m-3/2)\epsilon) - \epsilon \frac{\partial{}}{\partial s_i} E(s(t + (m-1)\epsilon)) \\ \qquad s_i(t + m\epsilon) &= s_i(t) + \epsilon \phi_i(t + (m-1/2)\epsilon) \\ \phi_i(t + n\epsilon) &= \phi_i(t + (n-1/2)\epsilon) - \frac{\epsilon}{2} \frac{\partial{}}{\partial s_i} E(s(t + n\epsilon)) \end{aligned}$$The inner-loop defined above is implemented by the following
leapfrog function, with pos, vel and step replacing
$s,\phi$ and $\epsilon$ respectively.
def leapfrog(pos, vel, step):
# one full velocity step
dE_dpos = tt.grad(energy_fn(pos).sum(), pos)
new_vel = vel - step * dE_dpos
# one full position step
new_pos = pos + step * new_vel
return [new_pos, new_vel],{}
The simulate_dynamics function performs the full algorithm. We start with the initial half-step update of $\phi$
and full-step of $s$, and then scan over the leapfrog method n_steps-1 times.
def simulate_dynamics(initial_pos, initial_vel, stepsize, n_steps, energy_fn):
def leapfrog(pos, vel, step):
# Gradient calculation
dE_dpos = at.grad(energy_fn(pos).sum(), pos)
new_vel = vel - step * dE_dpos
new_pos = pos + step * new_vel
return [new_pos, new_vel], {}
# An initial half-step in velocity
initial_energy = energy_fn(initial_pos)
dE_dpos = at.grad(initial_energy.sum(), initial_pos)
vel_half_step = initial_vel - 0.5 * stepsize * dE_dpos
# ... followed by one full position step
pos_full_step = initial_pos + stepsize * vel_half_step
# Perform full velocity-step updates afterwards, using scan
(all_pos, all_vel), scan_updates = scan(leapfrog,
outputs_info=[
dict(initial=pos_full_step),
dict(initial=vel_half_step),
],
non_sequences=[stepsize],
n_steps=n_steps - 1)
# Our final position after integrating
final_pos = all_pos[-1]
final_vel = all_vel[-1]
# One final half-step in velocity to complete the algorithm
energy = energy_fn(final_pos)
final_vel = final_vel - 0.5 * stepsize * at.grad(energy.sum(), final_pos)
# return new proposal state
return final_pos, final_vel
A final half-step is performed to compute $\phi(t+n\epsilon)$, and the final proposed state $\chi'$ is returned.
hmc_move
The hmc_move function implements the remaining steps (steps 1 and
3) of an HMC move proposal (while wrapping the simulate_dynamics
function). Given a matrix of initial states
$s \in \mathcal{R}^{N \times D}$ (positions) and energy function
$E(s)$ (energy_fn), it defines the symbolic graph for computing
n_steps of HMC, using a given stepsize. The function prototype
is as follows:
def hmc_move(s_rng, positions, energy_fn, stepsize, n_steps):
# sample random velocity using independent normals
initial_vel = s_rng.normal(size=positions.shape)
# perform simulation of particles subject to Hamiltonian dynamics
final_pos, final_vel = simulate_dynamics(
initial_pos=positions,
initial_vel=initial_vel,
stepsize=stepsize,
n_steps=n_steps,
energy_fn=energy_fn)
# accept/reject the proposed move based on the joint distribution
accept = metropolis_hastings_accept(
energy_prev=hamiltonian(positions, initial_vel, energy_fn),
energy_next=hamiltonian(final_pos, final_vel, energy_fn),
s_rng=s_rng)
return accept, final_pos
We start by sampling random velocities, using the provided shared
RandomStream object. Velocities are sampled independently for each
dimension and for each particle under simulation, yielding a
$N \times D$ matrix.
initial_vel = s_rng.normal(size=positions.shape)
Since we now have an initial position and velocity, we can now call the
simulate_dynamics to obtain the proposal for the new state $\chi'$.
final_pos, final_vel = simulate_dynamics(
initial_pos = positions,
initial_vel = initial_vel,
stepsize = stepsize,
n_steps = n_steps,
energy_fn = energy_fn)
We then accept/reject the proposed state based on the Metropolis algorithm.
accept = metropolis_hastings_accept(
energy_prev=hamiltonian(positions, initial_vel, energy_fn),
energy_next=hamiltonian(final_pos, final_vel, energy_fn),
s_rng=s_rng)
where metropolis_hastings_accept and hamiltonian are helper
functions, defined as follows.
def metropolis_hastings_accept(energy_prev, energy_next, s_rng):
ediff = energy_prev - energy_next
return (at.exp(ediff) - s_rng.uniform(size=energy_prev.shape)) >= 0
def kinetic_energy(vel):
return 0.5 * (vel ** 2).sum(axis=1)
def hamiltonian(pos, vel, energy_fn):
"""
Returns the Hamiltonian (sum of potential and kinetic energy) for the given
velocity and position. Assumes mass is 1.
"""
return energy_fn(pos) + kinetic_energy(vel)
hmc_move finally returns the tuple (accept, final_pos).
accept is a symbolic boolean variable indicating whether or not the
new state final_pos should be used or not.
hmc_updates
The purpose of hmc_updates is to generate the list of updates to
perform, whenever our HMC sampling function is called. hmc_updates
thus receives as parameters, a series of shared variables to update
(positions, stepsize and avg_acceptance_rate), and the
parameters required to compute their new state.
def hmc_updates(positions, stepsize, avg_acceptance_rate, final_pos,
accept, target_acceptance_rate, stepsize_inc, stepsize_dec,
stepsize_min, stepsize_max, avg_acceptance_slowness):
accept_matrix = accept.dimshuffle(0, *(('x',) * (final_pos.ndim - 1)))
new_positions = tt.switch(accept_matrix, final_pos, positions)
Using the above code, the dictionary {positions: new_positions} can
be used to update the state of the sampler with either (1) the new state
final_pos if accept is True, or (2) the old state if accept
is False. This conditional assignment is performed by Aesara's
switch
function.
switch expects as its first argument, a boolean mask with the same
broadcastable dimensions as the second and third argument. Since
accept is scalar-valued, we must first use
dimshuffle
to permute the dimensions so that it is of the appropriate
dimensions for broadcasting.
hmc_updates additionally implements an adaptive version of HMC. We start by
tracking the average acceptance rate of the HMC move proposals (across
many simulations), using an exponential moving average with time
constant 1 - avg_acceptance_slowness.
new_acceptance_rate = tt.add(
avg_acceptance_slowness * avg_acceptance_rate,
(1.0 - avg_acceptance_slowness) * accept.mean())
If the average acceptance rate is larger than the
target_acceptance_rate, we increase the stepsize by a factor
of stepsize_inc in order to increase the mixing rate of our chain.
If the average acceptance rate is too low however, stepsize is
decreased by a factor of stepsize_dec, yielding a more conservative
mixing rate.
_new_stepsize = tt.switch(avg_acceptance_rate > target_acceptance_rate,
stepsize * stepsize_inc, stepsize * stepsize_dec)
new_stepsize = tt.clip(_new_stepsize, stepsize_min, stepsize_max)
The
clip
function allows us to maintain the stepsize in the range
[stepsize_min, stepsize_max].
The final updates list is then returned:
return [(positions, new_positions),
(stepsize, new_stepsize),
(avg_acceptance_rate, new_acceptance_rate)]
import aesara
def hmc_updates(positions, stepsize, avg_acceptance_rate, final_pos, accept,
target_acceptance_rate, stepsize_inc, stepsize_dec,
stepsize_min, stepsize_max, avg_acceptance_slowness):
"""
POSITION UPDATES
Uses results of the acceptance test to update position
"""
accept_matrix = accept.dimshuffle(0, *(('x',) * (final_pos.ndim - 1)))
# if accept is True, update to `final_pos` else stay put
new_positions = at.switch(accept_matrix, final_pos, positions)
"""
STEP SIZE UPDATES
If the acceptance rate is two low, reduce the stepsize; if it is too high,
increase the stepsize
"""
_new_stepsize = at.switch(avg_acceptance_rate > target_acceptance_rate,
stepsize * stepsize_inc, stepsize * stepsize_dec)
# maintain stepsize in [stepsize_min, stepsize_max]
new_stepsize = at.clip(_new_stepsize, stepsize_min, stepsize_max)
# Update acceptance rate with exponential moving average
mean_dtype = aesara.scalar.upcast(accept.dtype, avg_acceptance_rate.dtype)
new_acceptance_rate = at.add(
avg_acceptance_slowness * avg_acceptance_rate,
(1.0 - avg_acceptance_slowness) * accept.mean(dtype=mean_dtype))
return [(positions, new_positions),
(stepsize, new_stepsize),
(avg_acceptance_rate, new_acceptance_rate)]
HMC_sampler
We implement the sampler in a Python class, called HMC_Sampler. It is a convenience wrapper for performing Hybrid Monte Carlo (HMC). It creates the symbolic graph for performing an HMC simulation (using hmc_move and hmc_updates). The graph is then compiled into the simulate function, an Aesara function which runs the simulation and updates the required shared
variables. Its main attributes are:
new_from_shared_positions: a constructor method which allocates various shared variables and strings together the calls tohmc_moveandhmc_updates. It also builds the Aesara functionsimulate, whose sole purpose is to execute the updates generated byhmc_updates.draw: a convenience method which calls the Aesara functionsimulateand returns a copy of the contents of the shared variableself.positions.
sharedX = lambda X, name: \
shared(np.asarray(X, dtype=aesara.config.floatX), name=name)
class HMC(object):
def __init__(self, shared_positions, energy_fn,
initial_stepsize=0.01, target_acceptance_rate=.9, n_steps=20,
stepsize_dec=0.98,
stepsize_min=0.001,
stepsize_max=0.25,
stepsize_inc=1.02,
avg_acceptance_slowness=0.9,
seed=12345):
self.positions = shared_positions
# allocate shared variables
self.stepsize = stepsize = sharedX(initial_stepsize, 'hmc_stepsize')
self.avg_acceptance_rate = avg_acceptance_rate = sharedX(target_acceptance_rate,
'avg_acceptance_rate')
s_rng = at.random.utils.RandomStream(seed)
# define graph for an `n_steps` HMC simulation
accept, final_pos = hmc_move(
s_rng,
shared_positions,
energy_fn,
stepsize,
n_steps)
# define the dictionary of updates, to apply on every `simulate` call
simulate_updates = hmc_updates(
shared_positions,
stepsize,
avg_acceptance_rate,
final_pos=final_pos,
accept=accept,
stepsize_min=stepsize_min,
stepsize_max=stepsize_max,
stepsize_inc=stepsize_inc,
stepsize_dec=stepsize_dec,
target_acceptance_rate=target_acceptance_rate,
avg_acceptance_slowness=avg_acceptance_slowness)
# compile Aesara function
self.simulate = function([], [], updates=simulate_updates)
def draw(self, **kwargs):
"""
Returns a new position obtained after `n_steps` of HMC simulation.
"""
self.simulate()
return self.positions.get_value(borrow=False)
Testing our Sampler¶
We test our implementation of HMC by sampling from a multi-variate
Gaussian distribution. We start by generating a random mean vector
mu and covariance matrix cov, which allows us to define the
energy function of the corresponding Gaussian distribution:
gaussian_energy. We then initialize the state of the sampler by
allocating a position shared variable. It is passed to the
constructor of HMC_sampler along with our target energy function.
Following a burn-in period, we then generate a large number of samples and compare the empirical mean and covariance matrix to their true values.
# Simulation hyperparameters
burnin=2000
n_samples=1000
dim=5
batchsize=3
Let's set up the model: a multivariate normal distribution.
rng = np.random.RandomState(123)
# Define a covariance and mu for a gaussian
mu = np.array(rng.rand(dim) * 10, dtype=aesara.config.floatX)
cov = np.array(rng.rand(dim, dim), dtype=aesara.config.floatX)
cov = (cov + cov.T) / 2.
cov[np.arange(dim), np.arange(dim)] = 1.0
cov_inv = np.linalg.inv(cov)
# Define energy function for a multi-variate Gaussian
def gaussian_energy(x):
return 0.5 * (at.dot((x - mu), cov_inv) * (x - mu)).sum(axis=1)
# Declared shared random variable for positions
position = shared(rng.randn(batchsize, dim).astype(aesara.config.floatX))
Now, let's initialize our sampler:
sampler = HMC(position, gaussian_energy,
initial_stepsize=1e-3, stepsize_max=0.5)
Execute some tuning samples, to be discarded.
burn_me = [sampler.draw() for r in range(burnin)]
Now draw n_samples for inference. This returns a tensor of dimension (n_samples, batchsize, dim).
samples = np.asarray([sampler.draw() for r in range(n_samples)])
samples.shape
flat_samples = samples.T.reshape(dim, -1).T
print('****** TARGET VALUES ******')
print('target mean:', mu)
print('target cov:\n', cov)
print('****** EMPIRICAL MEAN/COV USING HMC ******')
print('empirical mean: ', flat_samples.mean(axis=0))
print('empirical_cov:\n', np.cov(flat_samples.T))
print('****** HMC INTERNALS ******')
print('final stepsize', sampler.stepsize.get_value())
print('final acceptance_rate', sampler.avg_acceptance_rate.get_value())
As can be seen above, the samples generated by our HMC sampler yield an
empirical mean and covariance matrix, which are very close to the true
underlying parameters. The adaptive algorithm also seemed to work well
as the final acceptance rate is close to our target of 0.9.
References¶
- Team TTD, Al-Rfou R, Alain G, et al. (2016) Theano: A Python framework for fast computation of mathematical expressions. arXiv.org.
- Neal, R. M. (2010) MCMC using Hamiltonian dynamics, in the Handbook of Markov Chain Monte Carlo, S. Brooks, A. Gelman, G. L. Jones, and X.-L. Meng (editors), Chapman & Hall / CRC Press, pp. 113-162.
- Betancourt, M. (2017). A Conceptual Introduction to Hamiltonian Monte Carlo. arXiv.org.