Lattices of compatibly embedded finite fields in Nemo/Flint¶
Demonstrating lattices of compatibly embedded finite fields in Nemo.
Jupyter¶
- This Jupyter Notebook is available on Binder at https://github.com/erou/Nemo-embeddings-demo
- Press
Alt + rto enter/quit slide mode if you are using the RISE extension - every cells are interactive so you can play around
5*8
40
Nemo and Flint¶
A quick taste of Julia:
function foo(L)
m = L[1]
for i in 2:length(L)
if m < L[i]
m = L[i]
end
end
return m
end
foo (generic function with 1 method)
L = [2, 4, 1, 5, 7, 11, 3]
foo(L)
11
Nemo and Flint¶
using Nemo
Welcome to Nemo version 0.14.3 Nemo comes with absolutely no warranty whatsoever
We can play with standard mathematical objects
p = 13
k, x = FiniteField(p, 4, "x")
R, T = PolynomialRing(k, "T")
P = rand(R, 3)
(5*x^3+x^2+8*x+8)*T^3+(6*x^3+9*x^2+9*x+8)*T^2+(9*x^2+5*x+10)*T+(6*x^3+12*x^2+5*x+1)
The embedding problem¶
Example inspired by "On the powers of 2" [Granger, Kleinjung, Zumbrägel '14].
Let $P$ be an irreducible polynomial in $\mathbb F_{13^4}[T]$
P = T^4+(8*x^3+6*x^2+12*x+2)*T^3+(8*x^3+3*x^2+2*x+2)*T^2+(2*x^3+5*x^2+7*x+12)*T+(3*x^3+4*x^2+6*x+5)
factor(P)
1 * (T^4+(8*x^3+6*x^2+12*x+2)*T^3+(8*x^3+3*x^2+2*x+2)*T^2+(2*x^3+5*x^2+7*x+12)*T+(3*x^3+4*x^2+6*x+5))
We really want to factor it in degree $2$ factors in $\mathbb F_{13^8}[U]$:
K, y = FiniteField(p, 8, "y")
S, U = PolynomialRing(K, "U")
Q = S(P)
factor(Q)
1 * (T^2+(12*y^7+2*y^6+4*y^5+2*y^4+2*y^3+4*y^2+y+7)*T+(5*y^6+2*y^5+2*y^4+9*y^3+6*y+2)) * (T^2+(12*y^7+2*y^6+8*y^5+4*y^4+3*y^3+11*y^2+6)*T+(5*y^7+7*y^6+8*y^5+5*y^4+7*y^3+4*y^2+9*y+2))
The embedding problem¶
- $f$ irreducible polynomial of degree $m$ in $\mathbb F_p[X]$
- $g$ irreducible polynomial of degree $n$ in $\mathbb F_p[Y]$
- $m\;|\;n$
- $E = \mathbb F_p[X]/(f(X))$
- $F = \mathbb F_p[Y]/(g(Y))$
- Embedding problem: how to compute the embedding from $E$ to $F$ ?
Description and evaluation¶
[Brieulle, De Feo, Doliskani, Flori, Schost '17]
Two steps:
- Description: find $\alpha_1, \alpha_2$ such that:
- $E = \mathbb F_p(\alpha_1)$
- there exists an embedding $\phi:E\to F$ mapping $\alpha_1\mapsto\alpha_2$
- Evaluation:
- Compute $\phi(\gamma)\in F$ for $\gamma\in E$
- Test if $\delta\in\phi(E)$ for $\delta\in F$
- If $\delta\in\phi(E)$, compute $\phi^{-1}(\delta)\in E$
Description - naive algorithm¶
Context:
- $E = \mathbb{F}_p[X]/(f)$
- $F=\mathbb{F}_p[Y]/(g)$
Algorithm:
- Find a root $\rho$ of $f$ in $F$
- $\alpha_1 = \overline X$
- $\alpha_2 = \rho$
Other algorithms exist:
- [Lenstra '91]
- [Allombert '02]
- [Rains '96]
- [Narayanan '18]
Description - naive algorithm¶
Compute an embedding with embed.
E, x = FiniteField(13, 6, "x")
F, y = FiniteField(13, 12, "y")
ϕ = embed(E, F)
Morphism from Finite field of degree 6 over F_13 to Finite field of degree 12 over F_13
and evaluate it
ϕ(x)
6*y^11+8*y^10+8*y^9+9*y^8+9*y^7+9*y^6+3*y^5+y^4+7*y^3+8*y^2+4
Some sanity checks¶
We can check that ϕ is indeed a morphism:
a = rand(E)
b = rand(E)
ϕ(a^2 + b^7) == ϕ(a)^2 + ϕ(b)^7
true
and that the image of ϕ is in the subfield of $F$ with $13^6$ elements
ϕ(a)^(13^6) == ϕ(a), ϕ(b)^(13^6) == ϕ(b)
(true, true)
The end ?¶

No! ¶
The compatibility problem¶
Context:
- $E$, $F$, $G$ fields
- $E$ subfield of $F$ and $F$ subfield of $G$
- $\phi_{E\hookrightarrow F}$, $\phi_{F\hookrightarrow G}$, $\phi_{E\hookrightarrow G}$ embeddings
 $\phi_{F\hookrightarrow G}\circ\phi_{E\hookrightarrow F}\overset{?}{=}\phi_{E\hookrightarrow G}$
$\phi_{F\hookrightarrow G}\circ\phi_{E\hookrightarrow F}\overset{?}{=}\phi_{E\hookrightarrow G}$
The compatibility problem¶
Solutions:
- Conway polynomials [Parker '90], [Heath, Loehr '98]
- used in Magma, Sage, PARI, ...
- only practical with small finite fields
- Bosma, Cannon and Steel framework [Bosma, Cannon, Steel '97]
Bosma, Cannon and Steel framework¶
- Allows to work with arbitrary, user-defined finite fields
- Allows to build the embeddings in arbitrary order
- Used in MAGMA
- based on the naive algorithm
Bosma, Cannon and Steel framework¶

- Consider $\alpha$ such that $F=\mathbb{F}_p(\alpha)$
- Take $\rho$ a root of $\phi_{E\hookrightarrow G}(\text{Minpoly}_E(\alpha))$
- Map $\alpha\mapsto\rho$
Bosma, Cannon and Steel framework¶
It works with multiple subfields!
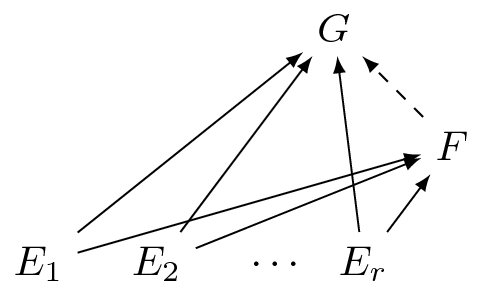
- Consider $\alpha$ such that $F=\mathbb{F}_p(\alpha)$
- Take $\rho$ a root of $\text{gcd}_i(\phi_{E_i\hookrightarrow G}(\text{Minpoly}_{E_i}(\alpha)))$
- Map $\alpha\mapsto\rho$
The compatibility problem¶
We define some finite fields $E = \mathbb F_{p^2}$, $F = \mathbb F_{p^4}$ and $G = \mathbb F_{p^8}$.
p = 5
E, x2 = FiniteField(p, 2, "x2")
F, x4 = FiniteField(p, 4, "x4")
G, x8 = FiniteField(p, 8, "x8")
(Finite field of degree 8 over F_5, x8)
and we compute the embeddings $\phi_{E\hookrightarrow F}$, $\phi_{F\hookrightarrow G}$, $\phi_{E\hookrightarrow G}$
ϕE_F = embed(E, F)
ϕE_G = embed(E, G)
ϕF_G = embed(F, G)
Morphism from Finite field of degree 4 over F_5 to Finite field of degree 8 over F_5
The compatibility problem¶
Morphisms are compatible!
a = rand(E)
ϕE_G(a) == (ϕF_G ∘ ϕE_F)(a)
true
The compatibility problem II¶
 $\phi_{G\hookrightarrow H}\circ\phi_{E\hookrightarrow G}\overset{?}{=}\phi_{F\hookrightarrow H}\circ\phi_{E\hookrightarrow F}$
$\phi_{G\hookrightarrow H}\circ\phi_{E\hookrightarrow G}\overset{?}{=}\phi_{F\hookrightarrow H}\circ\phi_{E\hookrightarrow F}$
The compatibility problem II¶
We create new finite fields
G, x6 = FiniteField(p, 6, "x6")
H, x12 = FiniteField(p, 12, "x12")
(Finite field of degree 12 over F_5, x12)
and embeddings between them
ϕE_G = embed(E, G)
ϕF_H = embed(F, H)
ϕG_H = embed(G, H)
Morphism from Finite field of degree 6 over F_5 to Finite field of degree 12 over F_5
The compatibility problem II¶
Morphisms are still compatible!
a = rand(E)
(ϕG_H ∘ ϕE_G)(a) == (ϕF_H ∘ ϕE_F)(a)
true
Implicit conversion¶
We do not need to explicitly call embed. Standard object oriented conversion also works.
k3, x3 = FiniteField(p, 3, "x3")
k24, x24 = FiniteField(p, 24, "x24")
(Finite field of degree 24 over F_5, x24)
z = k24(x3)
3*x24^23+4*x24^22+3*x24^20+4*x24^19+3*x24^18+3*x24^17+2*x24^14+4*x24^12+x24^11+4*x24^10+2*x24^9+4*x24^8+3*x24^6+3*x24^5+2*x24^4+4*x24^3+x24^2+1
z^(p^3) == z
true
k3(z)
x3
Sections¶
We can also compute sections of morphisms.
k7, x7 = FiniteField(p, 7, "x7")
k21, x21 = FiniteField(p, 21, "x21")
(Finite field of degree 21 over F_5, x21)
f7_21 = embed(k7, k21)
Morphism from Finite field of degree 7 over F_5 to Finite field of degree 21 over F_5
s21_7 = section(f7_21)
Section from Finite field of degree 21 over F_5 to Finite field of degree 7 over F_5
Sections¶
Sections give the preimage of an element if it is in the codomain of the embedding
a = rand(k7)
(s21_7 ∘ f7_21)(a) == a
true
And throw an error otherwise
s21_7(x21)
ArgumentError: not an element in the subfield of degree 7 over F_5
Stacktrace:
[1] (::Nemo.FinFieldSection{FqNmodFiniteField})(::fq_nmod) at /home/erou/.julia/packages/Nemo/gWAgl/src/FinFieldsTypes.jl:49
[2] top-level scope at In[26]:1
Sections¶
This can also be called implicitly
k7(k21(x7))
x7
k7(x21)
ArgumentError: not an element in the subfield of degree 7 over F_5
Stacktrace:
[1] (::Nemo.FinFieldSection{FqNmodFiniteField})(::fq_nmod) at /home/erou/.julia/packages/Nemo/gWAgl/src/FinFieldsTypes.jl:49
[2] (::FqNmodFiniteField)(::fq_nmod) at /home/erou/.julia/packages/Nemo/gWAgl/src/flint/fq_nmod.jl:462
[3] top-level scope at In[28]:1
Behind the scenes¶
- root finding is done by Flint (in C)
- minimal polynomials are computed by Nemo (in Julia)
- additionnal requirements of Bosma, Cannon and Steel framework are done in Nemo
- (almost) all the time is spent in root finding
- embedding evaluation is done via matrix-vector multiplication
More features planned¶
- Vector space morphisms,
- Algorithmic improvements,
- more efficient framework using Lenstra/Allombert embedding algorithm as building block
