In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
from scipy.stats import binom, poisson, zscore
Coming into the Fight¶
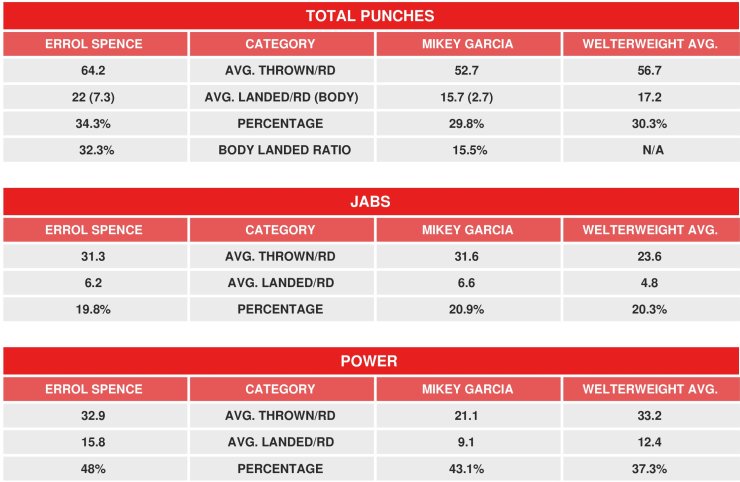
source: https://www.boxingscene.com/errol-spence-vs-mikey-garcia-compubox-historical-review--137148
(mis)Using Poisson to Get an Idea of Expected Fighter Output¶
Spence could be expected to be busier, but by how much and where?
In [2]:
np.random.seed(8)
sim_cnt_poi = 10000
spence_tot_poi, spence_jab_poi, spence_pow_poi = np.random.poisson(64, sim_cnt_poi), \
np.random.poisson(31, sim_cnt_poi), \
np.random.poisson(33, sim_cnt_poi)
garcia_tot_poi, garcia_jab_poi, garcia_pow_poi = np.random.poisson(53, sim_cnt_poi), \
np.random.poisson(32, sim_cnt_poi), \
np.random.poisson(21, sim_cnt_poi)
plt.figure(figsize=(16,6))
# SPENCE
ax1 = plt.subplot(231)
plt.hist(spence_tot_poi, 14, density=True, color='green')
plt.title("Spence Total Punches/Rd")
ax2 = plt.subplot(232, sharey=ax1)
plt.hist(spence_jab_poi, 14, density=True, color='green')
plt.title("Spence Jabs/Rd")
ax3 = plt.subplot(233, sharey=ax1)
plt.hist(spence_pow_poi, 14, density=True, color='green')
plt.title("Spence Power Punches/Rd")
# GARCIA
plt.subplot(234, sharex=ax1, sharey=ax1)
plt.hist(garcia_tot_poi, 14, density=True)
plt.title("Garcia Total Punches/Rd")
plt.subplot(235, sharex=ax2, sharey=ax1)
plt.hist(garcia_jab_poi, 14, density=True)
plt.title("Garcia Jabs/Rd")
plt.subplot(236, sharex=ax3, sharey=ax1)
plt.hist(garcia_pow_poi, 14, density=True)
plt.title("Garcia Power Punches/Rd")
plt.tight_layout()
A look at actual thrown performance v expectations¶
In [3]:
spence_total_thrown = [46, 55, 75, 89, 86, 95, 70, 102, 121, 125, 118, 100]
spence_jabs_thrown = [39, 43, 53, 61, 62, 56, 50, 60, 56, 58, 45, 35]
spence_power_thrown = [7, 12, 22, 28, 24, 39, 20, 42, 65, 67, 73, 65]
garcia_total_thrown = [12, 28, 31, 35, 41, 43, 26, 41, 32, 62, 15, 40]
garcia_jabs_thrown = [9, 13, 18, 20, 17, 19, 10, 22, 17, 25, 2, 16]
garcia_power_thrown = [3, 15, 13, 15, 24, 24, 16, 19, 15, 37, 13, 24]
A tale of two jabs: Spence pumped out that lead left at a ridiculous rate, neutralizing Garcia while setting-up the rest of his own offense¶
In [4]:
def chance_of_throwing_GE(sim, act):
return [np.sum(sim >= x)/len(sim) for x in act]
spence_comp_thrown = [(spence_tot_poi, spence_total_thrown), (spence_jab_poi, spence_jabs_thrown), (spence_pow_poi, spence_power_thrown)]
garcia_comp_thrown = [(garcia_tot_poi, garcia_total_thrown), (garcia_jab_poi, garcia_jabs_thrown), (garcia_pow_poi, garcia_power_thrown)]
print("SPENCE")
for spence in spence_comp_thrown:
spence_perf = chance_of_throwing_GE(spence[0], spence[1])
print(spence_perf, np.mean(spence_perf))
print("\nGARCIA")
for garcia in garcia_comp_thrown:
garcia_perf = chance_of_throwing_GE(garcia[0], garcia[1])
print(garcia_perf, np.mean(garcia_perf))
SPENCE [0.9912, 0.882, 0.0963, 0.0015, 0.005, 0.0001, 0.2386, 0.0, 0.0, 0.0, 0.0, 0.0] 0.18455833333333335 [0.093, 0.0245, 0.0001, 0.0, 0.0, 0.0, 0.0009, 0.0, 0.0, 0.0, 0.011, 0.2537] 0.031933333333333334 [1.0, 1.0, 0.9827, 0.8285, 0.9537, 0.1682, 0.9959, 0.0747, 0.0, 0.0, 0.0, 0.0] 0.5003083333333334 GARCIA [1.0, 1.0, 0.9997, 0.9969, 0.9615, 0.9309, 1.0, 0.9615, 0.9992, 0.1232, 1.0, 0.9713] 0.9120166666666667 [1.0, 0.9999, 0.9971, 0.9905, 0.9981, 0.995, 1.0, 0.9725, 0.9981, 0.9089, 1.0, 0.9991] 0.9882666666666666 [1.0, 0.927, 0.978, 0.927, 0.283, 0.283, 0.8865, 0.6958, 0.927, 0.0008, 0.978, 0.283] 0.6807583333333332
What about contact? "Everyone's gotta plan until they get hit."¶
In [5]:
s_plot = 1
fig = plt.figure(figsize=(16,6))
for stat in ((406, .298, "Garcia total", 75), (188, .209, "Garcia jabs", 21), (218, .431, "Garcia power", 54)):
n, p, category, N = stat[0], stat[1], stat[2], stat[3]
x = np.arange(binom.ppf(0.025, n, p),
binom.ppf(0.975, n, p))
sim_bouts = 10000
print("95 percent range for %s: \t" % category, int(np.min(x)), " - ", int(np.max(x)))
print("\t %s actually landed: \t" % category, N)
print("\t prob of landing this %s count or less:" % category,
"{0:.0f}%".format(np.sum(np.random.binomial(n, p, sim_bouts) < N)/float(sim_bouts) * 100))
ax = fig.add_subplot(1,3,s_plot)
ax.plot(x, binom.pmf(x, n, p), 'ro', ms=5, label='binom pmf')
plt.title(category)
ax.vlines(x, 0, binom.pmf(x, n, p), colors='r', lw=5, alpha=0.5)
ax.vlines(N, 0, np.max(binom.pmf(x, n, p)), lw=3, linestyles=":")
s_plot += 1
plt.tight_layout()
plt.show()
95 percent range for Garcia total: 103 - 138 Garcia total actually landed: 75 prob of landing this Garcia total count or less: 0% 95 percent range for Garcia jabs: 29 - 49 Garcia jabs actually landed: 21 prob of landing this Garcia jabs count or less: 0% 95 percent range for Garcia power: 80 - 107 Garcia power actually landed: 54 prob of landing this Garcia power count or less: 0%
Both fighters had their rates affected but while Mikey fell off the chart, almost literally and in a bad sense, Spence's superiour activity with the jab allowed him to set up and deliver the power punches, especially in volume over the second half of the bout¶
In [6]:
s_plot = 1
fig = plt.figure(figsize=(16,6))
for stat in ((1082, .343, "Spence total", 345), (618, .198, "Spence jabs", 108), (464, .480, "Spence power", 237)):
n, p, category, N = stat[0], stat[1], stat[2], stat[3]
x = np.arange(binom.ppf(0.025, n, p),
binom.ppf(0.975, n, p))
sim_bouts = 10000
print("95 percent range for %s: \t" % category, int(np.min(x)), " - ", int(np.max(x)))
print("\t %s actually landed: \t" % category, N)
print("\t prob of landing this %s count or less:" % category,
"{0:.0f}%".format(np.sum(np.random.binomial(n, p, sim_bouts) < N)/float(sim_bouts) * 100))
ax = fig.add_subplot(1,3,s_plot)
ax.plot(x, binom.pmf(x, n, p), 'go', ms=5, label='binom pmf')
plt.title(category)
ax.vlines(x, 0, binom.pmf(x, n, p), colors='g', lw=5, alpha=0.5)
ax.vlines(N, 0, np.max(binom.pmf(x, n, p)), lw=3, linestyles=":")
s_plot += 1
plt.tight_layout()
plt.show()
95 percent range for Spence total: 341 - 401 Spence total actually landed: 345 prob of landing this Spence total count or less: 4% 95 percent range for Spence jabs: 103 - 141 Spence jabs actually landed: 108 prob of landing this Spence jabs count or less: 7% 95 percent range for Spence power: 202 - 243 Spence power actually landed: 237 prob of landing this Spence power count or less: 90%
One more look at thrown punches¶
In [7]:
def standardized_fight_night(sim_rds, poi_lambda, n_times, act):
act_rds = len(act)
fight_night_zscore = np.zeros(act_rds)
for i in range(n_times):
fight_night_zscore += zscore(np.append(np.random.poisson(poi_lambda, sim_rds), act))[-act_rds:]
return fight_night_zscore/n_times
spence_total_zscore = standardized_fight_night(60, 64, 100, spence_total_thrown)
spence_total_zscore
Out[7]:
array([-1.42441765, -0.84977684, 0.42720275, 1.32108846, 1.12954152,
1.70418233, 0.10795785, 2.15112519, 3.36425579, 3.61965171,
3.17270886, 2.02342723])
In [8]:
garcia_total_zscore = standardized_fight_night(60, 53, 100, garcia_total_thrown)
garcia_total_zscore
Out[8]:
array([-3.40959768, -1.96473539, -1.69382371, -1.33260814, -0.79078479,
-0.610177 , -2.14534318, -0.79078479, -1.60351982, 1.10559696,
-3.138686 , -0.88108868])
In [9]:
plt.plot(spence_total_zscore, garcia_total_zscore, 'go')
Out[9]:
[<matplotlib.lines.Line2D at 0x245153e6f98>]
In [ ]:

