from IPython.core.display import HTML
print("Setting custom CSS for the IPython Notebook")
styles = open('custom.css', 'r').read()
HTML(styles)
Setting custom CSS for the IPython Notebook
import scipy
import numpy as np
import matplotlib
%matplotlib inline
%pylab inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context("talk")
sns.set_style("white")
import pandas as pd
from matplotlib.colors import ListedColormap
import sklearn
import sklearn.decomposition
import sklearn.neighbors
import sklearn.datasets
cmap_light = matplotlib.colors.ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
Populating the interactive namespace from numpy and matplotlib
# generate plots for later
# ML in 10 minutes plot
#cheat to get the same "random" numbers
np.random.seed(seed=99)
# make some data up
mean1 = [3,3]
mean2 = [8,8]
cov = [[1.0,0.0],[0.0,1.0]]
#create some points
x1 = np.random.multivariate_normal(mean1,cov,50)
x2 = np.random.multivariate_normal(mean2,cov,50)
plt.scatter(x1[:,0],x1[:,1], c='r', s=100)
plt.scatter(x2[:,0],x2[:,1], c='b', s=100)
plt.plot([2,10],[10,1], c='g', linewidth=5.0)
plt.title("ML in One Picture")
plt.xlabel("feature 1")
plt.ylabel("feature 2")
fig_ml_in_10 = plt.gcf()
# features matter plot
#cheat to get the same "random" numbers
np.random.seed(seed=99)
# make some data up
mean1 = [6,6]
mean2 = [6,6]
cov = [[1.0,0.0],[0.0,1.0]]
#create some points
x1 = np.random.multivariate_normal(mean1,cov,50)
x2 = np.random.multivariate_normal(mean2,cov,50)
plt.scatter(x1[:,0],x1[:,1], c='r', s=100)
plt.scatter(x2[:,0],x2[:,1], c='b', s=100)
plt.plot([2,10],[10,1], c='g', linewidth=5.0)
plt.title("Apples and Oranges")
plt.xlabel("Roundness")
plt.ylabel("Weight")
fig_features_matter_confused = plt.gcf()
#cheat to get the same "random" numbers
np.random.seed(seed=42)
# make some data up
mean1 = [5,5]
mean2 = [11,5]
cov = [[1.0,0.0],[0.0,1.0]]
#create some points
x1 = np.random.multivariate_normal(mean1,cov,50)
x2 = np.random.multivariate_normal(mean2,cov,50)
plt.scatter(x1[:,0],x1[:,1], c='r', s=100)
plt.scatter(x2[:,0],x2[:,1], c='b', s=100)
plt.plot([8,8],[2,10], c='g', linewidth=5.0)
plt.title("Apples and Oranges")
plt.xlabel("Color")
plt.ylabel("Shape")
fig_features_matter_separated = plt.gcf()
#cheat to get the same "random" numbers
np.random.seed(seed=99)
# make some data up
mean1 = [3,3]
mean2 = [8,8]
cov = [[1.0,0.0],[0.0,1.0]]
#create some points
x1 = np.random.multivariate_normal(mean1,cov,50)
x2 = np.random.multivariate_normal(mean2,cov,50)
plt.scatter(x1[:,0],x1[:,1], c='r', s=100)
plt.scatter(x2[:,0],x2[:,1], c='b', s=100)
plt.scatter([6],[9], c='k', s=200)
plt.plot([2,10],[10,1], c='g', linewidth=5.0)
plt.title("ML in One Picture")
plt.xlabel("feature 1")
plt.ylabel("feature 2")
fig_prediction = plt.gcf()
Introduction to Machine Learning¶
Analyze training data
Make predictions for new data points
- supervised learning
- data has labels
Find patterns in the data
- unsupervised learning
- data has no labels
Examples for Supervised Learning¶
- face detection
- handwritten digit recognition
- sound classification for hearing aids
- spam filtering
- recommender systems
Examples for Unsupervised Learning¶
- dimensionality reduction
- cocktail party problem
- fraud detection
- google image search categories
Somewhere in Between¶
reinforcement learning
- flappy bird agent
semi-supervised learning
- music classification
Supervised Learning¶
fig_ml_in_10
Features Matter!¶
fig_features_matter_confused
Features Matter!¶
fig_features_matter_separated
Self Driving Car¶
- *** What features do you need to drive a car? ***
Self Driving Car¶

Just Measure Everything?¶
Data volume
Computational overhead
Curse of Dimensionality
Prediction¶
fig_prediction
# get the data
x = np.concatenate((x1, x2))
# get the labels
ones = np.ones((50,))
y = np.concatenate((ones*0, ones))
K Nearest Neighbors¶
predict class of new data point by majority vote of K nearest neighbors
very simple
but good performance
K Nearest Neighbors¶
"train" a KNN Classifier¶
*** Why is this not really training? ***
k = 1 # number of neighbors
classifier = sklearn.neighbors.KNeighborsClassifier(n_neighbors=k)
classifier.fit(x,y)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
n_neighbors=1, p=2, weights='uniform')
Predict a Label¶
newPoint_1 = np.array([6,9])
newPoint_2 = np.array([2,4])
print classifier.predict([newPoint_1, newPoint_2])
fig_ml_in_10
[ 1. 0.]
Visualize the Decision Boundary¶
# code based on sklearn example
def visualize_decision_boundary(classifier, xmin, xmax, ymin,
ymax, step_size=0.02,
cmap=cmap_light):
xx, yy = np.meshgrid(np.arange(xmin, xmax, step_size),
np.arange(ymin, ymax, step_size))
colors = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
colors = colors.reshape(xx.shape)
ax = plt.subplot(111)
ax.pcolormesh(xx, yy, colors, cmap=cmap)
return ax
xx, yy = np.meshgrid(np.arange(0, 10, 2),
np.arange(0, 10, 2))
plt.scatter(xx,yy, c='b', zorder=2)
random_colors = np.random.randint(10, size=25)
random_colors = random_colors.reshape(xx.shape)
plt.pcolormesh(xx,yy,random_colors,cmap=plt.cm.Pastel2, zorder=1)
<matplotlib.collections.QuadMesh at 0x1735eb38>
# now visualize the boundary
boundary_vis = visualize_decision_boundary(classifier=classifier,
xmin=-2,xmax=12,
ymin=0,ymax=12,
step_size=0.02)
# and plot our data points
boundary_vis.scatter(x1[:,0],x1[:,1], c='r', s=100)
boundary_vis.scatter(x2[:,0],x2[:,1], c='b', s=100)
plt.show()
Now with Real Data¶
data = sklearn.datasets.fetch_mldata('MNIST original')
print data.keys()
x = data['data'][::50,:]
y = data['target'][::50]
print x.shape, y.shape
['data', 'COL_NAMES', 'DESCR', 'target'] (1400L, 784L) (1400L,)
What Are We Looking At?¶
# shuffle the data
randomized_data = np.random.permutation(x)
rows = 5
cols = 10
img = []
for col in xrange(rows, rows*cols, rows):
examples = randomized_data[col-rows:col,:]
col_img = np.reshape(examples,(28*rows,28))
img.append(col_img)
plt.imshow(np.hstack(img))
plt.show()
Scatter plot¶
data = sklearn.datasets.fetch_mldata('MNIST original')
x = data['data'][::50,:]
y = data['target'][::50]
svd = sklearn.decomposition.TruncatedSVD(n_components=2)
x = x - np.mean(x, axis=0)
#x = x / (np.std(x, axis=0) + 0.00001)
foo = svd.fit(x)
x_2d = foo.transform(x)
plt.scatter(x_2d[:,0], x_2d[:,1], c=y, s = 50, cmap=plt.cm.Paired)
plt.colorbar()
plt.show()
print foo_c
print "##########"
print pca_c
[[ -9.03875513e-17 3.22866312e-16 -9.26072909e-17 ..., -0.00000000e+00
-0.00000000e+00 -0.00000000e+00]
[ -1.72407198e-16 -1.54383212e-16 2.76140307e-16 ..., -0.00000000e+00
-0.00000000e+00 -0.00000000e+00]]
##########
[[ -5.98928482e-21 5.71049496e-19 3.80699664e-19 ..., 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[ 3.36892550e-21 -1.69759848e-19 2.82933081e-20 ..., 0.00000000e+00
0.00000000e+00 0.00000000e+00]]
Just Two Classes¶
x_sub_2d = x_2d[np.logical_or(y==8, y==0),:]
y_sub = y[np.logical_or(y==8, y==0)]
plt.scatter(x_sub_2d[:,0], x_sub_2d[:,1], c=y_sub,
s = 50, cmap=plt.cm.Paired)
plt.show()
Effect of K¶
k = 1
knn = sklearn.neighbors.KNeighborsClassifier(n_neighbors=k,
weights = 'uniform')
knn.fit(x_sub_2d,y_sub)
boundary_vis = visualize_decision_boundary(classifier=knn,
xmin=500, xmax=4000,
ymin=-2500,ymax=1500,
step_size=20.0, cmap=plt.cm.Paired)
# and plot our data points
boundary_vis.scatter(x_sub_2d[:,0], x_sub_2d[:,1],
c=y_sub, s = 10, linewidth=1,
cmap=plt.cm.Paired)
fig_knn = plt.gcf()
General Observations¶
For K=1:
- wiggly decision boundary
- can be changed by one data point
- high variance, low bias
For K >> 1:
- smoother boundary
- training error > 0
- low variance, high bias
Discussion:¶
- *** What are strengths and weaknesses of KNN? ***
- *** When would you use it? ***
- *** When would you not use it? ***
How Can We Choose K?¶
- best prediction performance
- generalization to unseen data
- need to measure performance
Error Measures¶
positive class: 8
negative class: 0
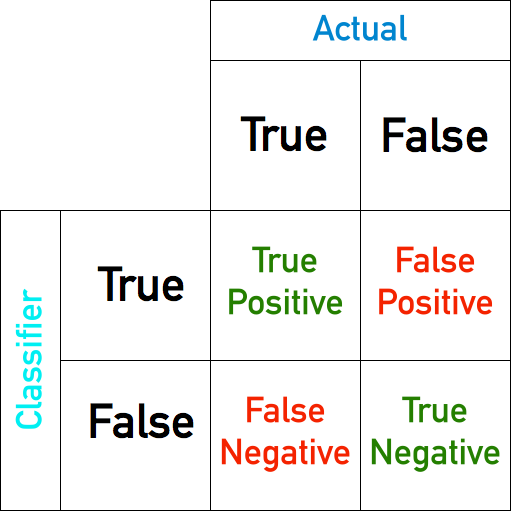
true positive (tp)
true negative (tn)
false positive (fp)
false negative (fn)
Confusion Matrix¶
k = 20
knn = sklearn.neighbors.KNeighborsClassifier(n_neighbors=k,
weights = 'uniform')
knn.fit(x_sub_2d,y_sub)
y_hat = knn.predict(x_sub_2d)
confusion_matrix = sklearn.metrics.confusion_matrix(y_sub, y_hat)
print confusion_matrix
# Show confusion matrix in a separate window
def show_confusion_matrix(confusion_matrix):
plt.matshow(confusion_matrix, cmap=plt.cm.Greys_r)
plt.title('Confusion matrix')
plt.colorbar()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
show_confusion_matrix(confusion_matrix)
k = 20
knn = sklearn.neighbors.KNeighborsClassifier(n_neighbors=k,
weights = 'uniform')
knn.fit(x,y)
y_hat = knn.predict(x)
confusion_matrix = sklearn.metrics.confusion_matrix(y, y_hat)
show_confusion_matrix(confusion_matrix)
print confusion_matrix
Accuracy for Multi Class¶
$$ \frac{N_{\text{true}}}{N_{\text{all}}} $$sklearn.metrics.accuracy_score(y, y_hat, normalize=True)
Evaluate Choice of K¶
def accuracy_for_k(k,x,y):
knn = sklearn.neighbors.KNeighborsClassifier(n_neighbors=k,
weights = 'uniform')
knn.fit(x,y)
y_hat = knn.predict(x)
return sklearn.metrics.accuracy_score(y, y_hat, normalize=True)
## Why is this code inefficient?
acc_values = []
k_values = xrange(1,50,2)
for k in k_values:
acc_values.append(accuracy_for_k(k=k,x=x_sub_2d,y=y_sub))
plt.plot(k_values, acc_values)
plt.xlabel('Value of k')
plt.ylabel('Accuracy')
fig_train_acc = plt.gcf()
Closer Look¶
- *** Why does the accuracy drop ? ***
- *** Why is this plot meaningless? ***
fig_train_acc
With Validation Set¶
def accuracy_for_k_val(k,x,y, random_state=99):
split_data = sklearn.cross_validation.train_test_split(
x,y, test_size=0.33, random_state=random_state)
x_train, x_val, y_train, y_val = split_data
knn = sklearn.neighbors.KNeighborsClassifier(n_neighbors=k,
weights = 'uniform')
knn.fit(x_train,y_train)
y_hat = knn.predict(x_val)
return sklearn.metrics.accuracy_score(y_val, y_hat,
normalize=True)
acc_values_val = []
acc_values_train = []
k_values = xrange(1,150,2)
for k in k_values:
acc_values_train.append(accuracy_for_k(k=k,x=x_sub_2d,y=y_sub))
acc_values_val.append(accuracy_for_k_val(k=k,x=x_sub_2d,y=y_sub))
plt.plot(k_values, acc_values_train, c='r', label="training accuracy")
plt.plot(k_values, acc_values_val, c='b', label="validation accuracy")
plt.xlabel('Value of k')
plt.ylabel('Accuracy')
plt.legend()
fig_cross_val = plt.gcf()
Overfitting¶
- worse for flexible models
- model captures noise in training data
- low training error
- high prediction error
- countermeasures:
- regularization *** - Where is this in KNN? ***
- cross validation
fig_knn
Cross Validation¶
- split data into three sub-sets
- train: to train the model
- validation: to tune hyper-parameters
- test: to evaluate prediction performance
Cross Validation¶
*** When do you not need a validation set? ***
*** Why do we need a train and a validation set? ***
*** Why do we need an extra test set? ***
*** Why could Rafael be upset with my plot? ***
fig_cross_val
Better Cross Validation¶
- Measurements without error bars do not exist!
- Split the data multiple times
k_values = range(1,150,10)
np.random.seed(seed=99)
random_seeds = np.random.randint(1000, size=50)
values = np.zeros((len(k_values),random_seeds.shape[0]))
for k, c_k in zip(k_values, range(len(k_values))):
counter_rs = 0
for rs,c_rs in zip(random_seeds, range(random_seeds.shape[0])):
value = accuracy_for_k_val(k=k,x=x_sub_2d,y=y_sub,
random_state=rs)
values[c_k,c_rs] = value
sns.tsplot(values.T)
plt.xlabel('k')
plt.ylabel('accuracy')
plt.show()
k_values = range(1,150,10)
np.random.seed(seed=99)
random_seeds = np.random.randint(1000, size=50)
values = np.zeros((len(k_values),random_seeds.shape[0]))
for k, c_k in zip(k_values, range(len(k_values))):
counter_rs = 0
for rs,c_rs in zip(random_seeds, range(random_seeds.shape[0])):
value = accuracy_for_k_val(k=k,x=x_sub_2d,y=y_sub,
random_state=rs)
values[c_k,c_rs] = value
sns.boxplot(values.T)
plt.xlabel('k')
plt.ylabel('accuracy')
plt.show()
Classifiers and Invariance¶
- digit recognition is
- translation invariant
- rotation invariant (a little bit)
Ways to Handle Invariance:¶
- add transformation to training data
- introduce canonical representation
- build into classifier
Rotation Invariance:¶

Tangent Space¶

Elements of Statistical Learning¶

Pattern Recognition Class¶
by Fred Hamprecht
on Youtube
http://www.youtube.com/playlist?list=PLuRaSnb3n4kRDZVU6wxPzGdx1CN12fn0w
