%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from bs4 import BeautifulSoup
import requests
from pattern import web
import scipy.stats as stats
import statsmodels.api as sm
from scipy.stats import binom
from __future__ import division
import re
from StringIO import StringIO
from zipfile import ZipFile
from pandas import read_csv
#nice defaults for matplotlib
from matplotlib import rcParams
dark2_colors = [(0.10588235294117647, 0.6196078431372549, 0.4666666666666667),
(0.8509803921568627, 0.37254901960784315, 0.00784313725490196),
(0.4588235294117647, 0.4392156862745098, 0.7019607843137254),
(0.9058823529411765, 0.1607843137254902, 0.5411764705882353),
(0.4, 0.6509803921568628, 0.11764705882352941),
(0.9019607843137255, 0.6705882352941176, 0.00784313725490196),
(0.6509803921568628, 0.4627450980392157, 0.11372549019607843),
(0.4, 0.4, 0.4)]
rcParams['figure.figsize'] = (10, 6)
rcParams['figure.dpi'] = 150
rcParams['axes.color_cycle'] = dark2_colors
rcParams['lines.linewidth'] = 2
rcParams['axes.grid'] = True
rcParams['axes.facecolor'] = '#eeeeee'
rcParams['font.size'] = 14
rcParams['patch.edgecolor'] = 'none'
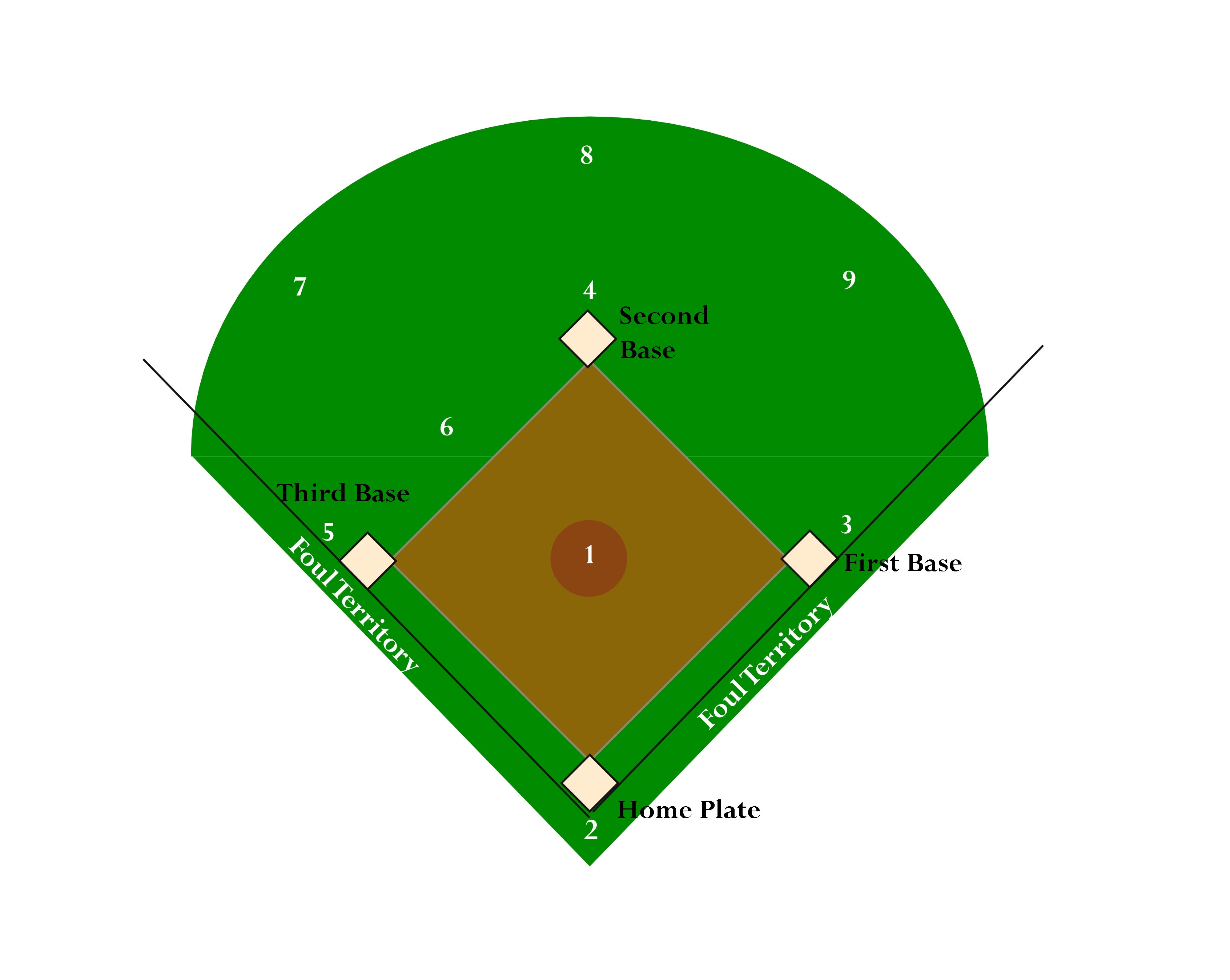
Some Terms¶
- R - Runs
- AB - At bats
- SO - Strike out
- H - Hitter puts the ball in play and is not out
- 2B - Hitter gets to second
- 3B - Hitter gets to third
- HR - Home Run, hitter scores a run
- BB - Base on balls
- PA - Plate apperances $\approx$ AB+BB
Tables¶
zip_folder = requests.get('http://seanlahman.com/files/database/lahman-csv_2014-02-14.zip').content
zip_files = StringIO()
zip_files.write(zip_folder)
csv_files = ZipFile(zip_files)
teams = csv_files.open('Teams.csv')
teams = read_csv(teams)
players = csv_files.open('Batting.csv')
players = read_csv(players)
salaries = csv_files.open('Salaries.csv')
salaries = read_csv(salaries)
dat = teams[(teams['G'] == 162) & (teams['yearID']<2002) ]
dat[["teamID","yearID", "H", "2B", "3B", "HR", "BB"]].head()
| teamID | yearID | H | 2B | 3B | HR | BB | |
|---|---|---|---|---|---|---|---|
| 437 | DET | 1904 | 1231 | 154 | 69 | 11 | 344 |
| 1366 | LAA | 1961 | 1331 | 218 | 22 | 189 | 681 |
| 1367 | KC1 | 1961 | 1342 | 216 | 47 | 90 | 580 |
| 1377 | NYA | 1962 | 1509 | 240 | 29 | 199 | 584 |
| 1379 | LAA | 1962 | 1377 | 232 | 35 | 137 | 602 |
5 rows × 7 columns
players = players[players["yearID"]>=1947]
def f(series):
return series.index[np.where(series==min(series))][0]
df = players[players["AB"]>502]
grouped = df.groupby("playerID", as_index=False)
rookie_idx = grouped["yearID"].aggregate({'min_index':f})['min_index'].values
rookie = df.loc[rookie_idx][["playerID", "AB", "H"]]
grouped = df.drop(rookie_idx).groupby("playerID", as_index=False)
sophomore_idx = grouped["yearID"].aggregate({'min_index':f})['min_index'].values
sophomore = df.loc[sophomore_idx][["playerID", "AB", "H"]]
tab = pd.merge(rookie, sophomore, on='playerID', how='outer')
tab = tab.dropna()
tab["avg1"]=tab["H_x"]/tab["AB_x"]*1000
tab["avg2"]=tab["H_y"]/tab["AB_y"]*1000
plt.hist(tab["avg2"],bins=np.arange(200,380,10))
plt.ylabel("Frequency")
plt.xlabel("Sophomore batting averages")
plt.show()
avgs = tab["avg2"]
z = (avgs-np.mean(avgs))/np.std(avgs)
stats.probplot(z, dist="norm", plot=plt)
plt.title("Normal Q-Q plot")
plt.show()
Predict Batting Average for Sophomores¶
plt.scatter(tab["avg1"], tab["avg2"])
plt.xlabel("Rookie")
plt.ylabel("Sophomore")
plt.show()
Predict Batting Average for Sophomores¶
plt.scatter(tab["avg1"], tab["avg2"])
plt.xlabel("Rookie")
plt.ylabel("Sophomore")
plt.vlines(295, 150 ,400, color = 'red', alpha = 0.5)
plt.vlines(305, 150 ,400, color = 'red', alpha = 0.5)
plt.ylim(150,400)
plt.show()
tab["rounded_avg1"] = np.array([round(a/10,0)*10 for a in tab["avg1"].values])
df = tab[tab["rounded_avg1"]==300]
plt.hist(df["avg2"].values, bins=np.arange(200,380,10))
plt.vlines(np.mean(df["avg2"]), 0,20, color = 'Red', alpha = 0.7)
plt.xlabel("Sophomore averages in strata")
plt.show()
tab.boxplot(column = "avg2", by = "rounded_avg1")
plt.xlabel("Rookie average")
plt.ylabel("Sophomore average")
plt.xticks(rotation = 50)
plt.show()
grouped = tab.groupby("rounded_avg1", as_index=False)
tmp = grouped["avg2"].aggregate({'mean':np.mean})
plt.scatter(tmp["rounded_avg1"], tmp["mean"], s=40)
plt.plot(tmp["rounded_avg1"], tmp["rounded_avg1"], alpha = 0.6)
plt.xlim(249,351)
plt.ylim(249,351)
plt.show()
Regression Line¶
How do we predict $Y$ from $X$? $$ \frac{Y - \mu_Y}{\sigma_Y} = r \frac{X-\mu_X}{\sigma_X} $$
With
$$ r = \frac{1}{N} \sum_{i=1}^N \left( \frac{Y - \mu_Y}{\sigma_Y} \right) \left( \frac{X-\mu_X}{\sigma_X} \right) $$Here the correlation is 0.41.
We can also get this with least squares.
Improved prediction power¶
plt.boxplot([tab["avg2"], df["avg2"].values])
plt.xticks([1,2], ["All","Strata"])
plt.show()
Note the SD within strata is smaller:
$$\sqrt{ (1-r) \sigma_Y^2} \leq \sigma_Y $$Regression Fallacy¶
top10 = tab[["playerID","avg1", "avg2"]]
top10["avg1"] = np.array([round(a) for a in top10["avg1"].values])
top10["avg2"] = np.array([round(a) for a in top10["avg2"].values])
top10 = top10.sort("avg1", ascending = 0)
top10.head(10)
| playerID | avg1 | avg2 | |
|---|---|---|---|
| 896 | olerujo01 | 363 | 294 |
| 113 | boggswa01 | 361 | 325 |
| 210 | cashno01 | 361 | 243 |
| 1020 | rodrial01 | 358 | 300 |
| 751 | madlobi01 | 354 | 339 |
| 490 | gwynnto01 | 351 | 317 |
| 1135 | suzukic01 | 350 | 321 |
| 780 | mauerjo01 | 347 | 328 |
| 304 | davisto02 | 346 | 326 |
| 789 | mayswi01 | 345 | 319 |
10 rows × 3 columns
Regression Fallacy¶
bottom10 = top10.sort("avg1", ascending = 1)
bottom10.head(10)
| playerID | avg1 | avg2 | |
|---|---|---|---|
| 629 | joosted01 | 206 | 250 |
| 963 | priddje01 | 214 | 296 |
| 842 | moneydo01 | 222 | 284 |
| 533 | hernaen01 | 222 | 232 |
| 1117 | staubru01 | 224 | 280 |
| 132 | boyercl02 | 224 | 272 |
| 689 | lanieha01 | 226 | 213 |
| 871 | murphda05 | 226 | 281 |
| 160 | brunato01 | 227 | 254 |
| 1111 | stallvi01 | 228 | 254 |
10 rows × 3 columns
Moneyball¶
- How do we pick players?
# get all years with more than 162 games and before 2002
dat = teams[(teams["G"]==162) & (teams["yearID"]>=1947)]
avg = dat["H"]/dat["AB"]
plt.scatter(avg, dat["R"]/162)
plt.xlabel("Batting average")
plt.ylabel("Runs per game")
plt.show()
Batting Average is expensive¶
# compute lifetime totals for each player, then
# compute AVG, HR rates and BB rates
pdat = pd.merge(salaries, players, on=['yearID','playerID'], how='outer')
pdat = pdat.sort(["playerID","yearID"])
#remove invalid data
pdat = pdat.dropna(subset = ["teamID_x", "teamID_y"])
grouped = pdat.groupby("playerID", as_index=False)
pdat = grouped[["AB", "H", "HR", "BB", "salary"]].aggregate(np.sum)
pdat["salary"] = pdat["salary"]/1000000
pdat["AVG"] = np.array([min(max(240,pdat["H"][i]/pdat["AB"][i]*1000),320)
for i in range(len(pdat))])
pdat["HRR"] = pdat["HR"]/(pdat["AB"]+pdat["BB"])
pdat["BBR"] = pdat["BB"]/(pdat["AB"]+pdat["BB"])
pdat = pdat[pdat["AB"]>1000]
pdat["rounded_AVG"] = np.array([round(a,-1) for a in pdat["AVG"].values])
pdat.boxplot(column = "salary", by = "rounded_AVG")
plt.xlabel("Lifetime Batting Average")
plt.ylabel("Total Salary in Millions")
plt.show()
HR are expensive as well¶
pdat["rounded_HRR"] = np.array([round(a*1000,-1) for a in pdat["HRR"].values])
pdat.boxplot(column = "salary", by = "rounded_HRR")
plt.xlabel("Lifetime HR rate (per 1000 PA)")
plt.ylabel("Total Salary in Millions")
plt.show()
What else predicts runs?¶
dat = teams[(teams["G"]==162) & (teams["yearID"]>=1947)]
avg = dat["H"]/dat["AB"]
dat = dat[["R","H", "2B", "3B", "HR", "BB", "AB"]]
dat["H"] = dat["H"]-dat["2B"]-dat["3B"]-dat["HR"]
dat["PA"] = dat["BB"]+dat["AB"]
plt.scatter(avg, dat["R"]/162)
plt.xlabel("Average")
plt.ylabel("Runs per game")
plt.title("corr="+str(round(np.corrcoef(avg,dat["R"])[0][1],2)))
plt.show()
names = ["Singles","Doubles","Triples","HR","BB"]
i = 0
for col in dat.columns[1:6]:
plt.scatter(dat[col], dat["R"])
plt.xlabel(names[i])
i+=1
plt.ylabel("Runs per game")
plt.title("corr="+str(round(np.corrcoef(dat[col],dat["R"])[0][1],2)))
plt.show()
BBs are not as expensive¶
pdat["rounded_BBR"] = np.array([int(round(a*1000,-1)) for a in pdat["BBR"].values])
pdat.boxplot(column = "salary", by = "rounded_BBR" )
plt.xlabel("Lifetime BB rate (per 1000 PA)")
plt.ylabel("Total Salary in Millions")
plt.xticks(rotation = 50)
plt.show()
Prediction Model¶
$Y$=Runs, $X_1$=Singles, $X_2$=Doubles, $X_3$=Triples $X_4$=HR $X_5$=BB
Linear regression model:
$$ E( Y | X_1, \dots ,X_5) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \beta_4 X_4 +\beta_5 X_5 $$Further assumption:
$$ Y | X_1, \dots, X_5 = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \beta_4 X_4 +\beta_5 X_5 +\varepsilon$$with $\varepsilon \sim \mbox{IID}(0,\sigma^2)$
Fit the model with least squares¶
Pick the $\beta$ that minimize
$$ \sum_{i=1}^N \{Y_i - (\beta_0 + \beta_1 X_{i,1} + \beta_2 X_{i,2} + \beta_3 X_{i,3})\}^2 $$We use a hat, $\hat{\beta}$ to distinguish the real $\beta$ s from the estimated
Fit before 2002, test after¶
First notice there is a trend in runs
dat = teams[(teams['G']==162) & (teams['yearID']>=1947)]
plt.scatter(dat["yearID"], dat["R"]/162)
plt.xlabel("Year")
plt.ylabel("Runs per game")
plt.show()
Fit before 2002, test on 2002¶
We fit the model to data from before 2002 and fitted to data from 2002. We obtain the following mean squared errors:
dat["AVG"] = dat["H"]/dat["AB"]
dat["1B"] = dat["H"]-dat["2B"]-dat["3B"]-dat["HR"]
dat["PA"] = dat["BB"] + dat["AB"]
#Fit before 2002
dat1 = dat[(dat["yearID"]>=1947) & (dat["yearID"]<=2001)]
#test on 2002
dat2 = dat[dat["yearID"]==2002]
fit = []
Y = dat1["R"].values
X = np.transpose(dat1["AVG"].values)
X = sm.add_constant(X)
fit.append(sm.OLS(Y,X).fit())
X = np.transpose(dat1["HR"].values)
X = sm.add_constant(X)
fit.append(sm.OLS(Y,X).fit())
X = np.transpose([dat1["1B"].values,dat1["2B"].values,
dat1["3B"].values, dat1["HR"].values,
dat1["BB"].values])
X = sm.add_constant(X)
fit.append(sm.OLS(Y,X).fit())
names = ["Model based on "+name for name in ["AVG alone: ","HR alone: ","all five statistics: "]]
X = []
X.append(np.transpose(dat2["AVG"].values))
X.append(np.transpose(dat2["HR"].values))
X.append(np.transpose([dat2["1B"].values,dat2["2B"].values,
dat2["3B"].values, dat2["HR"].values,
dat2["BB"].values]))
for i in range(3):
X_new = sm.add_constant(X[i])
print names[i]+str(np.mean(fit[i].predict(X_new)-dat2["R"])**2)
Model based on AVG alone: 909.77129839 Model based on HR alone: 38.2867101892 Model based on all five statistics: 2.08324042148
Our fitted model is similar to OPS¶
$$ \mbox{predicted runs} = -457 + 0.53 \mbox{S} + 0.79 \mbox{D} + 1.16 \mbox{T} + 1.4 \mbox{HR} + 0.3764 \mbox{BB} $$On-base plus sluggin (OPS) is a popular summary invented by Sabermetricians: (BB+H)/PA + (S + 2D + 3T + 4HR)/ AB
dat1["OPS"] = (dat1["BB"]+dat1["H"])/dat1["PA"]+(dat1["1B"]+
2*dat1["2B"]+3*dat1["3B"]+4*dat1["HR"])/dat1["AB"]
fitted = fit[2].predict(sm.add_constant(np.transpose([dat1["1B"].values,dat1["2B"].values,
dat1["3B"].values, dat1["HR"].values,
dat1["BB"].values])))
plt.scatter(dat1["OPS"], fitted)
plt.xlabel("OPS")
plt.ylabel("Our prediction")
plt.title("correlation="+str(round(np.corrcoef(dat1["OPS"],fitted)[0][1],2)))
plt.show()
Stable metrics¶
For any player, there is variability in summaries across years.
pdat = players[(players["AB"]>=502) & (players["yearID"]>=1996)]
#players with 10 or more seasons with 502 at bats since 1996
grouped = pdat.groupby("playerID", as_index=False)
count = grouped["yearID"].aggregate({"N":np.size})
count = count[count["N"]>=10]["playerID"].values
pdat = pdat[pdat['playerID'].isin(count)]
pdat["AVG"] = pdat["H"]/pdat["AB"]
pdat["PA"] = pdat["BB"] + pdat["AB"]
pdat["1B"] = pdat["H"] - pdat["2B"] - pdat["3B"] - pdat["HR"]
pdat["OPS"] = (pdat["BB"]+pdat["H"])/pdat["PA"]+(pdat["1B"]+2*pdat["2B"]+3*pdat["3B"]+4*pdat["HR"])/pdat["AB"]
y = pdat[pdat["playerID"]=="jeterde01"]
plt.scatter(y["yearID"], y["AVG"]*1000, zorder = 1, s = 60)
plt.plot(y["yearID"], y["AVG"]*1000, zorder = 0)
plt.xlabel("Year")
plt.ylabel("AVG")
plt.title("Derek Jeter")
plt.show()
OPS slightly more stable than AVG¶
Note OPS is slightly better at distinguishing players
grouped = pdat.groupby("playerID", as_index = False)
avg = grouped["AVG"].aggregate({"mean_AVG":np.mean})
avg = avg.sort("mean_AVG")
idx = avg["playerID"].values
boxes = []
for playerID in idx:
df = pdat[pdat["playerID"]==playerID]
boxes.append(df["AVG"].values)
plt.boxplot(boxes)
plt.xticks(np.arange(1,23,1), idx, rotation=70)
plt.show()
grouped = pdat.groupby("playerID", as_index = False)
avg = grouped["OPS"].aggregate({"mean_OPS":np.mean})
avg = avg.sort("mean_OPS")
idx = avg["playerID"].values
boxes = []
for playerID in idx:
df = pdat[pdat["playerID"]==playerID]
boxes.append(df["OPS"].values)
plt.boxplot(boxes)
plt.xticks(np.arange(1,23,1), idx, rotation=70)
plt.show()