Section 1: Python Essentials¶

1.1. A brief introduction about programming languages¶

1.1.1. What's an algorithm?¶

1.1.2. What's a programming language?¶

We could say that it is a language we can use to communicate with a machine and ask about solving a specific task. We can specify an algorithm, that solves a task in a particular way, and make the machine execute and do what we need.

Ok, there are some differences between programming languages. There are (in general) two categories: (1) Compiled and (2) Interpreted programming languages.

Interpreted and compiled programming languages

We thought about an algorithm to go to our institute or university. In that example, we learnt that I mentioned that if you are most specific, the machine will not need to "infer" many things. It will not have to work too hard to understand what you asking to do. Then, the most specific you are, the fastest the execution of such an algorithm.

That's because of this abstraction level as we see here. Binary code is 0's and 1's, that's how machine operates over data and perform computations, but we cannot code directly in Binary Code.

If we increase the level of abstraction, we will see the Machine code and Assembly languages, which are still too complicated for humans to use directly on data analysis.

Then, we have the middle-level languages. Examples of that are C/C++ and FORTRAN. Here, the tasks are done very fast. And on top of them, we have high-level, scripting languages such as MATLAB, Java, and Python.

Compared to High-level or scripting languages such MATLAB and Python, C/C++ is super fast.

That's because in C you have access to very middle-level instructions (e.g., memory allocation). Which means you can be more specific about what the machine should do and how to do it. However, and very often, you have to code more in C/C++ than in Python. It takes longer... And your code is gonna be compiled. While others are interpreted.

Now, what are the differences between them?

1.1.3. What's Python?¶

• It is a high-level programming language that has an English-like syntax. This makes it easier to read!
• It is interpreted and it has dynamic semantics. It’s the Python Virtual Machine (the translator) that infers data types, functions, and so on.

1.1.3.1. Main advantages¶

Some of them are:

1.1.3.2. Main disadvantages¶

1.2. Python Essentials: A quick recap¶

1.2.1. What's Jupyter notebook?¶

(Image source: memgraph.com)

A notebook document can contain computer code (e.g., python scripts) and text elements (e.g., paragraph, equations, figures, links, etc). Thus, these documents contain analysis descriptions, results as well as executable cells which can be run to perform data analysis.

Here, we can directly "talk" to the Python's interpreter. You can run the code of a cell by selecting it and pressing "shift + enter". Try it out!

1.2.2. Variables and Python Data Types¶

1.2.2.1. Variables¶

We can think that a variable in programming is a name or a label that we will use to refer a particular object. Such object can be value we store in the memory (e.g. n = 15).

We can store values on variables without specifying their types. That's because Python is a dynamically-typed languague: If we assign a value to a variable the python interpreter will assign it a type.

For example, if we do this:

We can see with type() the type of each variable.

Note that we didn't specify explicitly the type of the data of each variable. Thus, the Python interpreter infers which data type is from the value you want to store.

You can also change the type of the variables:

Notice that was b = 7.1. However, we are forcing to convert a decimal value into an integer. Then, the interpreter truncates the original value.

1.2.2.2. Lists¶

1.2.2.2.1. Definition¶

Imagine that you want to store 100 values about an specific variable (e.g., participant_age, neuron_type). It is not convenient to create 100 variables to store each value.

In such cases, we use Python lists (also known as vectors or arrays).

For example:

Note that a list can store different types of elements.

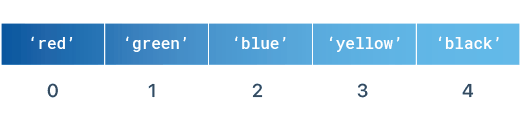
(Image source: LearnByExample.org)

1.2.2.2.2. List indexing¶

In order to have access to the elements of a given list, we should write the index of such element in the list, starting by the number 0.

For example:

Let's consider the following list of integers:

We can know the length of a list (i.e., the amount of elements it has) by writing len(my_list):

We can access each item by indicating its index:

1.2.2.2.3. Slicing¶

We can access to specific sub-list of a list.

If we write our_list[:a], it will return every element of our_list until the index a.

And also access to a sublist:

We can invert a Python list as follows:

1.2.2.2.4. Adding elements into a list¶

To add an element use append() as follows:

1.2.2.2.5. Removing elements from a list¶

You can remove an element from a list by indicating such element.

For example, to remove the element 9 we do:

Note that remove(item) will remove the first item it finds (not all of them) from left to right.

1.2.2.3. Nested lists¶

List allow us to store different types of variables such as Integers, Floats, Strings... and also lists! In this case, we call them nested lists.

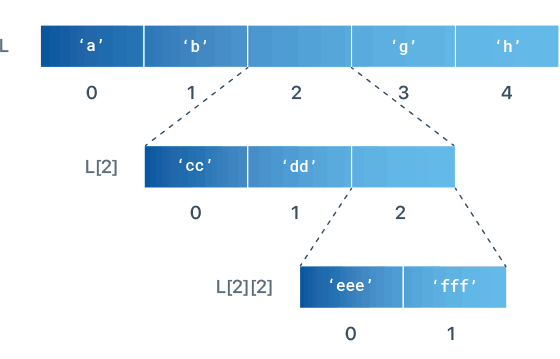
(Image source: LearnByExample.org)

Let's check the implementation of such example below:

We can also use this property to represent a matrix:

In this case, a matrix would be represented by a list of list.

1.2.2.4. Dictionaries¶

Python dictionaries (dict()) allow us to store information on them and using keys for indexing.

They are an unordered sequence of items, as pairs (key, value).

Just like Lists, the values of dictionaries can hold data of different types (i.e., integers, floats, strings, lists, dictionaries, etc).

For example:

Python dictionaries help us to store our data in complex data structures.

1.3. Python Control Statements and loops¶

1.3.1. Control Statements (if, elif, else)¶

In order to control the execution flow in your algorithm, in python we use if (condition), elif (condition), and else.

1.3.1.1. Syntax¶

if (condition):
  # your statements if `condition` is True
else:
  # your statements if `condition` is False

if one condition is not enough, we can do:

if (condition1):
  # your statements if `condition1` is True
else:
  # your statements if `condition1` is False
  if (condition2):
    # your statements if `condition2` is True
  else:
    # your statements if `condition2` is False

or equivalently:

if (condition1):
  # your statements if `condition1` is True
elif (condition2):
  # your statements if `condition1` is False but `condition2` is True
else:
  # your statements if both `condition1` and `condition2` are False

1.3.1.2. Example¶

1.3.2. Control Statements (for and while)¶

We can access each element of a list through for and while.

for allow us to repeat each element of an list or range.

For example:

On the other hand, while also loops but given a condition.

while (conditional_statement):
  # actions
  # ...

While such condition is True all the inner statements will be executed.

Note: Be sure that the condition will turn False at some point. Otherwise, the while loop will never end.

1.3.3. Exercise¶

Compute z as the substraction of each element of lists x and y, such that $z_i = (x_i - y_i)^2$. Assume that input lists x and y have the same length. Finally, print each value of z and its index in the list.

Use a repetition statement to access each element of the arrays.

Example input:

x = [1,2,3,4,5]
y = [2,2,2,2,2]

Expected output:

Index 0 , value: 1
Index 1 , value: 0
Index 2 , value: 1
Index 3 , value: 4
Index 4 , value: 9

Solution

Bonus: Compute the matrix multiplication of A = [[2,5,2],[1,0,-2],[3,1,1]] and B = [[-2,1,0],[-2,2,1],[0,0,3]] and save the result in C. Then, print each row of the matrix C.

Example input:

A = [[2,5,2],[1,0,-2],[3,1,1]]
B = [[-2,1,0],[-2,2,1],[0,0,3]]

Expected output:

[-14, 12, 11]
[ -2,  1, -6]
[ -8,  5,  4]

Solution

1.4. Functions¶

1.4.1. What's a function?¶

• A function is a block of code that runs when it is called.
• You can pass data (i.e, parameters) into a function.
• Functions are used to perform specific actions, and they are also known as methods.

1.4.2. Syntax¶

(Image source: LearnByExample)

1.4.3. How to create a function?¶

1.4.4. How to call a function?¶

A function can receive input parameters or arguments to perform computations. In that case, you should add those arguments separated by commas.

For example:

If you want to allow any amount of arguments, you define a function as follows:

Additionally, you can make it for keyword arguments:

A function can also return values by using the return statement:

1.4.5. Advantages of using functions¶

1. Modularity.
2. Decomposing complex problems into simpler pieces.
3. Reuse code, avoiding duplication.
4. Clousure.
5. Improving clarity.

1.4.6. Exercise¶

1. Write a function that receives two parameters: (1) v, a list of numbers, and (2) a, an scalar. The function should return a list y such that y = v*a.

Example input

v = [1,2,3,4,9,8,7,6,5] a = 10

_Expected output_
```python

[10, 20, 30, 40, 90, 80, 70, 60, 50]

Solution

(Bonus #1)

Write a function that returns the distance, as absolute value, between every pair of components between two lists x and y. Use abs(). Call such function and print the result, separating each row.

Example Input:

x=[1,2,3,4,5]; y=[1,2,3,4,5]

_Expected Output:_
```python

[0, 1, 2, 3, 4] [1, 0, 1, 2, 3] [2, 1, 0, 1, 2] [3, 2, 1, 0, 1] [4, 3, 2, 1, 0]

Solution Bonus #1

(Bonus #2)

3. Write a function that returns the multiplication of two matrices A and B (each one represented as a list of lists). Print each row of the resulting matrix separately.

Example Input:

A = [[1,2,3],[2,0,5],[8,0,0]] B = [[1,2,3],[1,2,3],[1,2,3]]

_Expected Output_
```python

[6, 12, 18] [7, 14, 21] [8, 16, 24]

Solution Bonus #2

1.5. Decorators¶

1.5.1. Definition¶

A decorator is a function that allow us to extend the behavior of another input function (without explicitly changing it).

1.5.2. Example¶

Let's consider the next function to sum to numbers a and b:

Let's try to extends its behavior and make it operate for a list of pairs (a,b).

As you saw, we did not need to change anything from our first function called add_together. Instead, we just added @decorator_name before its definition.

This helps a lot to expand the functionalities of your functions without the need of modifying them.

So, decorators are an elegant way to extend functionalities of your functoins without the need of modifying them!

(Spoiler) We will use decorators in more detail tomorrow. It will help us to speed-up our python code 🔥!.

1.5.3. Exercise¶

Given the function divide as follows:

Create a decorator called smart_divide(func) that receives as input the function called divide(a,b) and executes it only if b is not 0. Otherwise, print "I cannot divide!" and return None.

1.5.4. Solution¶

1.6. Practical part: Python built-in functions.¶

1.6.1. Section Exercise¶

A distance measure between two vectors as lists

Create a function called vector_distance that receives three input parameters:

• x: a list of integers.
• y: a list of integers.
• f: a function that operates two input parameters: a and b.

Then, vector_distance should return the mean distance after operating each pair of element (a,b) by the function f.

Note: assume that x and y have the same lengths (i.e., number of elements)

1.6.2. Solution¶

Try your implementation:

Bonus: A distance measure between two matrices as nested lists.

1. A distance function called matrix_distance which, instead of computing a distance f(a,b) receives as inputs two matrices X and Y as nested lists.

2. Create a function called matmut to multiply two matrices X and Y (nested lists).

3. Modify the previous function matmul to apply the function vector_distance instead of multiplying and sum the element of a row and a column.

1.7. Python modules¶

1.7.1. What is a Python module?¶

A python module is a reusable chunk of code that you may want to include in your programs / projects.

Compared to languages like C/C++, a Python libraries do not pertain to any specific context in Python.

Then, a library is a collection of modules.

1.7.2. Importing Python's modules¶

1.7.2.1. Math Module¶

1.7.2.2. Random Module¶

1.7.2.3. Time Module¶

Computation times usually fluctuate a lot. In order to have a better estimation we compute the mean (and standard deviation) of a vector of times.

Let's see this point with an example:

1.7.2.4. Exercises¶

Create function that returns a list of $n \geq 1$ random numbers between -1 and 1. Validate $n$: if $n$ is less than 1, then return an empty list.

(Bonus):

Measure the time needed to compute the sum of 1000 random numbers (in seconds).

Solution

1.8. Creating Python's modules¶

(Image source: Cognizant Softvision).

1.8.1. Introduction¶

You can create your own modules and packages in Python. This will make easier to maintain and debug your code.

Some of the benefits of modularizing your code are:

• Keeping a clear distritribution of functions you use, avoiding duplication.
• Sharing your code with colleagues or a community.
• You can show that a certain method works or an algorithm. For example: after finishing a paper, you can upload and make public the data and the code (if possible).
• Many others!

1.8.2. My first python module (Google Colab)¶

1.8.2.1. Creating a python module¶

Follow the next steps:

1. Go to "Files", to the right of "Table of contents" panel.
2. Do right-click and select "New file". We will create a python file (*.py). Name such file as my_python_module.py.
3. Do double left-click on it. A new panel will appear in our Colab user interface. There write your own module!.
4. We can start with the following code:

import random
def create_random_numbers(n):
    my_list = []
    for i in range(n):
        random_num = random.random()
        random_num = (random_num*2) - 1
        my_list.append( random_num )
    return my_list

1.8.2.2. Importing my python module¶

We can import the module as follows:

One way to see what is the content of your python module is by doing dir(your_module).

Let's use the function of my_python_lib

That's it!

By using modules, we can make our analysis more robust as we are leveraging existing code. When we create our modules, we can publish them and helps ourselves and other programmers/scientists to use them in future analyses 😀.

1.8.2.3. Exercise¶

Add and test the following function into your module called my_python_module:

def add_together(a, b):
    return a + b

1.8.2.4. Solution¶

Day #1 of the summer course "Introduction to High-Performance Computing in Python for Scientists!".

Goethe Research Academy for Early Career Researchers (GRADE), Goethe University Frankfurt, Germany. June 2022.