This is an interactive jupyter notebook document.
Page down through it, following the instructions…
With what looks to be a permanent and long-run partial moving-online of the university, the already important topic of “data science” seems likely to become even more foundational. Hence this first problem set tries to provide you with an introduction—to “data science”, and to the framework we will be using for problem sets that we hope will make things much easier for you and for us…
When you are finished, satisfied, or stuck, print your notebook to pdf, & email the pdf to us with subject line:
econ-115-f-2020-jupyter-notebook-0-
Please include whatever comments on this assignment you want us to know...
Problem Set 0. Python & Notebooks¶
These computer programming problem set assignments are a required part of the course.
Collaborating on the problem sets is more than okay—it is encouraged! Seek help from a classmate or an instructor or a roommate or a passerby when you get stuck! (Explaining things is beneficial, too—the best way to solidify your knowledge of a subject is to explain it.)
But the work has to be your own: no cutting-&-pasting from others' problem sets, please! We want you to learn this stuff, and your fingers typing every keystroke is an important way of building muscle memory here.
In fact, we strongly recommend that as you work through this notebook, whenever you come to a "code" cell—something intended not for you to read but also to direct the computer—the python interpreter—to do calculations, you (1) click on the code cell to bring it into your browser's focus; (2) click on the + button in the toolbar above to create a new code cell just below the one you were now in; and then (3) retype, line-by-line, the computer code in the cell (not the comment lines beginning with #s, but the code cells) while trying to figure out what the line of code is intended to tell the python interpreter to do. "Muscle"—in this case, fingertip—memory is an important but undervalued part of "active learning" here at Berkeley. In Germany, however, they have a term for it: das Fingerspitzengefühl; it's the kind of understanding-through-the-fingertips that a true expert has.
In this problem set, you will learn how to:
- navigate jupyter notebooks (like this one);
- write and evaluate some basic expressions in python, the computer language of the course;
- call functions to use code other people have written; and
- break down python code into smaller parts to understand it.
For reference, you might find it useful to read chapter 3 of the Data 8 textbook: <http://www.inferentialthinking.com/chapters/03/programming-in-python.html>. Chapters 1 <https://www.inferentialthinking.com/chapters/01/what-is-data-science.html> and 2 <https://www.inferentialthinking.com/chapters/02/causality-and-experiments.html> are worth skimming as well...
0. Why Are We Doing This?¶
First of all, we are doing this because our section leaders are overworked: teaching online takes more time and effort than teaching in person, and our section leaders were not overpaid before the 'rona arrived on these shores. Taking the bulk of the work of grading calculation assignments off of their backs is a plus—and it appears that the best way for us to do that is to distribute a number of the course assignements to you in this form: the form of a python computer language "jupyter notebook"
Second, we are doing this because learning jupyter notebooks and python may well turn out to be the intellectual equivalent for you of "eat your spinach": something that may seem unpleasant and unappetizing now, but that makes you stronger and more capable. In 1999 Python programming language creator Guido van Rossem compared the ability to read, write, and use software you had built or modified yourself to search and analyze data and information collectiosn to literacy (see Fernando Perez: When Python Becomes Pervasive https://www.youtube.com/watch?v=Wd6a3JIFH0s). He predicted that mass programming, if it could be attained, would produce increases in societal power and changes in societal organization of roughly the same magnitude as mass literacy has had over the past several centuries. Guido may be right, and he may be wrong. But what is clear is that your lives may be richer, and you may have more options, if the data science and basic programming intellectual tools become a useful part of your intellectual panoplies.
An analogy: An anology: Back in the medieval European university, people would learn the trivium—the “trivial” subjects of grammar (how to write), rhetoric (how to speak in public), and logic (how to think coherently)—then they would learn the quadrivium of arithmetic, geometry, music/harmony, and astronomy/astrology; and last they would learn the advanced and professional subjects: law or medicine or theology and phyics, metaphysics, and moral philosophy. But a student would also learn two more things: how to learn by reading—how to take a book and get something useful out of it, without a requiring a direct hands-on face-to-face teacher; and (2) how to write a fine chancery hand so that they could prepare their own documents, for submission to secular courts or to religious bishops or even just put them in a form where they would be easily legible to any educated audience back in those days before screens-and-attachments, before screens-and-printers, before typewriters, before printing.
The data science tools may well turn out to be in the first half of the 2000s the equivalent of a fine chancery hand, just as a facility with the document formats and commands of the Microsoft office suite were the equivalent of a fine chancery hand at the end of the 1900s: practical, general skills that make you of immense value to most if not nearly all organizations. This—along with the ability to absorb useful knowledge without requiring hands-on person-to-person face-to-face training—will greatly boost your social power and your set of opportunities in your life. If we are right about its value.
Third, why jupyter and python, rather than r-studio and r, or c++ and matlab? Because jupyter project founder Fernando Perez has an office on the fourth floor of Evans. Because 40% of Berkeley undergraduates currently take Data 8 and so, taking account of other channels, more than half of Berkeley students are already going to graduate literate in python.
Let us get started!
1. Jupyter notebooks¶
This webpage is called a Jupyter notebook. A notebook is a place to write programs and view their results, and also to write text.
A notebook is thus an editable computer document in which you can write computer programs; view their results; and comment, annotate, and explain what is going on. Project jupyter https://en.wikipedia.org/wiki/Project_Jupyter is headquartered here at Berkeley, where jupyter originator and ringmaster Fernando Pérez https://en.wikipedia.org/wiki/Fernando_Pérez_(software_developer) works: its purpose is to build human-friendly frameworks for interactive computing. If you want to see what Fernando looks and sounds like, you can load and watch a 15-minute inspirational video by clicking on "YouTubeVideo" below and then on the ▶ in the toolbar above:
from IPython.display import YouTubeVideo
# The original URL is:
# https://www.youtube.com/watch?v=Wd6a3JIFH0s
YouTubeVideo("Wd6a3JIFH0s")
1.1. Text cells¶
In a notebook, each rectangle containing text or code is called a cell.
Text cells (like this one) can be edited by double-clicking on them. They're written in a simple format created by Jon Gruber called markdown <http://daringfireball.net/projects/markdown/syntax> to add formatting and section headings. You almost surely want to learn how to use markdown.
After you edit a text cell, click the "run cell" button at the top that looks like ▶ in the toolbar at the top of this window, or hold down shift + press return, to confirm any changes to the text and formatting.
(Try not to delete the problem set instructions. If you do, then (a) rename your current notebook via the Rename command in the File menu so that you do not lose your work done so far, and then reenter the url http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=lecture-support-2020&branch=master&path=ps01.ipynb in the web address bar at the top of your browser to download a new, fresh copy of this problem set.)
Question 1.1.1. This paragraph is in its own text cell. Try editing it so that this sentence is the last sentence in the paragraph, and then click the "run cell" ▶| button or hold down shift + return. This sentence, for example, should be deleted. So should this one.
1.2. Code cells¶
Other cells contain code in the Python 3 language. Running a code cell will execute all of the code it contains.
To run the code in a code cell, first click on that cell to activate it. It'll be highlighted with a little green or blue rectangle. Next, either press ▶ or hold down shift + press return.
Try running this cell:
print("Hello, World!")
And this one:
print("\N{WAVING HAND SIGN}, \N{EARTH GLOBE ASIA-AUSTRALIA}!")
The fundamental building block of Python code is an expression. Cells can contain multiple lines with multiple expressions. When you run a cell, the lines of code are executed in the order in which they appear. Every print expression prints a line. Run the next cell and notice the order of the output.
print("First this line is printed,")
print("and then this one.")
Question 1.2.1. Change the cell above so that it prints out:
First this line,
then the whole 🌏,
and then this one.
Hint: If you're stuck on the Earth symbol for more than a few minutes, try talking to a neighbor or a staff member. That's a good idea for any lab problem.
1.3. Writing notebooks¶
You can use Jupyter notebooks for your own projects or documents. When you make your own notebook, you'll need to create your own cells for text and code.
To add a cell, click the + button in the menu bar. It'll start out as a text cell. You can change it to a code cell by clicking inside it so it's highlighted, clicking the drop-down box next to the restart (⟳) button in the menu bar, and choosing "Code".
Question 1.3.1. Add a code cell below this one. Write code in it that prints out:
A whole new cell! ♪🌏♪
(That musical note symbol is like the Earth symbol. Its long-form name is \N{EIGHTH NOTE}.)
Run your cell to verify that it works.
1.4. "Errors"¶
Python is a language, and like natural human languages, it has rules. It differs from natural language in two important ways:
- The rules are simple. You can learn most of them in a few weeks and gain reasonable proficiency with the language in a semester.
- The rules are rigid. If you're proficient in a natural language, you can understand a non-proficient speaker, glossing over small mistakes. A computer running Python code is not smart enough to do that.
Whenever you write code, you'll make mistakes. When you run a code cell that has errors, Python will sometimes produce error messages to tell you what you did wrong.
Errors are okay; even experienced programmers make many errors. When you make an error, you just have to find the source of the problem, fix it, and move on.
We have made an error in the next code cell. Run it and see what happens.
(Note: In the toolbar, there is the option to click Cell > Run All, which will run all the code cells in this notebook in order. However, the notebook stops running code cells if it hits an error, like the one in the cell just below.)
print("This line is missing something."
You should see something like this (minus our annotations):

The last line of the error output attempts to tell you what went wrong. The syntax of a language is its structure, and this SyntaxError tells you that you have created an illegal structure. "EOF" means "end of file," so the message is saying Python expected you to write something more (in this case, a right parenthesis) before finishing the cell.
There's a lot of terminology in programming languages, but you don't need to know it all in order to program effectively. If you see a cryptic message like this, you can often get by without deciphering it. (Of course, if you're frustrated, ask a neighbor or a staff member for help.)
Try to fix the code above so that you can run the cell and see the intended message instead of an error.
print("This line is missing something.")
1.5. Programming & testing¶
Our notebooks include built-in tests to check whether your work is correct. Sometimes, there are multiple tests for a single question, and passing all of them is required to receive credit for the question. Please don't change the contents of the test cells.
Run the next code cell to initialize the tests:
# run this code cell to initialize the OK tests capabilities...
from client.api.notebook import Notebook
ok = Notebook('ps00.ok')
Go ahead and attempt Question 1.5.1. Running the cell directly after it will test whether you have assigned seconds_in_a_decade correctly in Question 4.1. If you haven't, this test will tell you the correct answer. Resist the urge to just copy it, and instead try to adjust your expression. (Sometimes the tests will give hints about what went wrong...)
Question 1.5.1. Assign the name seconds_in_a_decade to the number of seconds between midnight January 1, 2010 and midnight January 1, 2020. Note that there are two leap years in this span of a decade. A non-leap year has 365 days and a leap year has 366 days.
Hint: If you're stuck, the next section shows you how to get hints.
# In the next line, replace the ellipsis ("...") after the equals sign ("=")
# with the number of seconds in a decade. Then click the
seconds_in_a_decade = ...
# Do not change anything else in this cell. Just click the "run cell" button
# that looks like `▶` in the toolbar at the top of this window, or hold down
# `shift` + press`return`:
print(seconds_in_a_decade)
ok.grade("q1_5_1");
If ok.grade found that you had set the right variable(s) to the proper value(s) that it expected, well and good: you are probably not far off track. If ok.grade reported that you failed any of the tests, go back and think again—and if you are still stuck, call for help.
1.6. The kernel¶
The kernel is a program that executes the code inside your notebook and outputs the results. In the top right of your window, you can see a circle that indicates the status of your kernel. If the circle is empty (⚪), the kernel is idle and ready to execute code. If the circle is filled in (⚫), the kernel is busy running some code.
Next to every code cell, you'll see some text that says In [...]. Before you run the cell, you'll see In [ ]. When the cell is running, you'll see In [*]. If you see an asterisk (*) next to a cell that doesn't go away, it's likely that the code inside the cell is taking too long to run, and it might be a good time to interrupt the kernel (discussed below). When a cell is finished running, you'll see a number inside the brackets, like so: In [1]. The number corresponds to the order in which you run the cells; so, the first cell you run will show a 1 when it's finished running, the second will show a 2, and so on.
You may run into problems where your kernel is stuck for an excessive amount of time, your notebook is very slow and unresponsive, or your kernel loses its connection. If this happens, try the following steps:
- At the top of your screen, click Kernel, then Interrupt.
- If that doesn't help, click Kernel, then Restart. If you do this, you will have to run your code cells from the start of your notebook up until where you paused your work.
- If that doesn't help, restart your server. First, save your work by clicking File at the top left of your screen, then Save and Checkpoint. Next, click Control Panel at the top right. Choose Stop My Server to shut it down, then Start My Server to start it back up. Then, navigate back to the notebook you were working on. You'll still have to run your code cells again.
1.7. Libraries¶
There are many add-ons and extensions to the core of python that are useful—indeed essential—to using it to get work done. They are contained in what are called libraries. The rest of this notebook needs three libraries. So let us tell the python interpreter to install them. Run the code cell below to do so:
# install the numerical python, python data analysis, and mathematical
# plotting libraries for python
!pip install numpy
!pip install pandas
!pip install matplotlib
import numpy as np
import pandas as pd
import matplotlib as mpl
1.8. Submitting your work¶
All problem sets in the course will be distributed as notebooks like this one, and you will submit your work from the notebook. We will use a system called OK that checks your work and helps you submit. At the top of each assignment, you'll see a cell like the one below that prompts you to identify yourself. Run it and follow the instructions. Please use your @berkeley.edu address when logging in.
# this cell will not yet give you directions as to how to login to the
# autograding system
#
# Later on, after we have hooked this notebook into the autograding
# system, we will reenable that functionality.
# Don't change this cell; just run it.
# The result will give you directions about how to log in to the submission system, called OK.
# Once you're logged in, you can run this cell again,
# but it won't ask you who you are because it remembers you.
# However, you will need to log in once per assignment.
# When you log-in please hit return (not shift + return) after typing in your email
from client.api.notebook import Notebook
ok = Notebook('ps00.ok')
When you finish an assignment, you need to submit it by running the submit command below. It's fine to submit multiple times. OK will only try to grade your final submission for each assignment. Don't forget to submit your lab assignment at the end of section, even if you haven't finished everything.
# this cell is currently "commented out": that is, we have turned the
# program line into a comment that the python interpreter believes it
# is supposed to ignore. Later on, after we have hooked this notebook
# into the autograding system, we will reenable it.
# _ = ok.submit()
2. Python: numbers & variables¶
Quantitative information arises everywhere in data science. In addition to representing commands to print out lines, expressions can represent numbers and methods of combining numbers. The expression 3.2500 evaluates to the number 3.25. (Run the cell and see.)
3.2500
Notice that we didn't have to print. When you run a notebook cell, if the last line has a value, then Jupyter helpfully prints out that value for you. However, it won't print out prior lines automatically.
print(2)
3
4
Above, you should see that 4 is the value of the last expression, 2 is printed, but 3 is lost forever because it was neither printed nor last.
You don't want to print everything all the time anyway. But if you feel sorry for 3, change the cell above to print it.
2.1. Arithmetic¶
The line in the next cell subtracts. Its value is what you'd expect. Run it.
3.25 - 1.5
Many basic arithmetic operations are built into Python. The textbook section on Expressions describes all the arithmetic operators used in the course. The common operator that differs from typical math notation is **, which raises one number to the power of the other. So, 2**3 stands for $2^3$ and evaluates to 8.
The order of operations is the same as what you learned in elementary school, and Python also has parentheses. For example, compare the outputs of the cells below. The second cell uses parentheses for a happy new year!
3+6*5-6*3**2*2**3/4*7
4+(6*5-(6*3))**2*((2**3)/4*7)
In standard math notation, the first expression is
$$3 + 6 \times 5 - 6 \times 3^2 \times \frac{2^3}{4} \times 7,$$while the second expression is
$$3 + (6 \times 5 - (6 \times 3))^2 \times (\frac{(2^3)}{4} \times 7).$$Question 2.1.1. Write a Python expression in this next cell that's equal to $5 \times (3 \frac{10}{11}) - 50 \frac{1}{3} + 2^{.5 \times 22} - \frac{7}{33} + 3$. That's five times three and ten elevenths, minus fifty and a third, plus two to the power of half twenty-two, minus seven thirty-thirds plus three. By "$3 \frac{10}{11}$" we mean $3+\frac{10}{11}$, not $3 \times \frac{10}{11}$.
Replace the ellipses (...) with your expression. Try to use parentheses only when necessary.
Hint: The correct output should start with a familiar number.
...
2.2. Variables¶
In natural language, we have terminology that lets us quickly reference very complicated concepts. We don't say, "That's a large mammal with brown fur and sharp teeth!" Instead, we just say, "Bear!"
In Python, we do this with assignment statements. An assignment statement has a name on the left side of an = sign and an expression to be evaluated on the right.
ten = 3 * 2 + 4
When you run that cell, Python first computes the value of the expression on the right-hand side, 3 * 2 + 4, which is the number 10. Then it assigns that value to the name ten. At that point, the code in the cell is done running.
After you run that cell, the value 10 is bound to the name ten:
ten
The statement ten = 3 * 2 + 4 is not asserting that ten is already equal to 3 * 2 + 4, as we might expect by analogy with math notation. Rather, that line of code changes what ten means; it now refers to the value 10, whereas before it meant nothing at all.
If the designers of Python had been ruthlessly pedantic, they might have made us write
define the name ten to hereafter have the value of 3 * 2 + 4
instead. You will probably appreciate the brevity of "="! But keep in mind that this is the real meaning.
Question 2.2.1. Try writing code that uses a name (like eleven) that hasn't been assigned to anything. You'll see an error!
...
A common pattern in Jupyter notebooks is to assign a value to a name and then immediately evaluate the name in the last line in the cell so that the value is displayed as output.
close_to_pi = 355/113
close_to_pi
Another common pattern is that a series of lines in a single cell will build up a complex computation in stages, naming the intermediate results.
semimonthly_salary = 841.25
monthly_salary = 2 * semimonthly_salary
number_of_months_in_a_year = 12
yearly_salary = number_of_months_in_a_year * monthly_salary
yearly_salary
Names in Python can have letters (upper- and lower-case letters are both okay and count as different letters), underscores, and numbers. The first character can't be a number (otherwise a name might look like a number). And names can't contain spaces, since spaces are used to separate pieces of code from each other.
Other than those rules, what you name something doesn't matter to Python. For example, this cell does the same thing as the above cell, except everything has a different name:
a = 841.25
b = 2 * a
c = 12
d = c * b
d
However, names are very important for making your code readable to yourself and others. The cell above is shorter, but it's totally useless without an explanation of what it does.
2.3. Application: a physics experiment¶
On the Apollo 15 mission to the Moon, astronaut David Scott famously replicated Galileo's physics experiment in which he showed that gravity accelerates objects of different mass at the same rate. Because there is no air resistance for a falling object on the surface of the Moon, even two objects with very different masses and densities should fall at the same rate. David Scott compared a feather and a hammer.
You can run the following cell to watch a video of the experiment.
from IPython.display import YouTubeVideo
# The original URL is:
# https://www.youtube.com/watch?v=U7db6ZeLR5s
YouTubeVideo("U7db6ZeLR5s")
Here's the transcript of the video:
167:22:06 Scott: Well, in my left hand, I have a feather; in my right hand, a hammer. And I guess one of the reasons we got here today was because of a gentleman named Galileo, a long time ago, who made a rather significant discovery about falling objects in gravity fields. And we thought where would be a better place to confirm his findings than on the Moon. And so we thought we'd try it here for you. The feather happens to be, appropriately, a falcon feather for our Falcon. And I'll drop the two of them here and, hopefully, they'll hit the ground at the same time.
167:22:43 Scott: How about that!
167:22:45 Allen: How about that! (Applause in Houston)
167:22:46 Scott: Which proves that Mr. Galileo was correct in his findings.
Newton's Law. Using this footage, we can also attempt to confirm another famous bit of physics: Newton's law of universal gravitation. Newton's laws predict that any object dropped near the surface of the Moon should fall
$$\frac{1}{2} G \frac{M}{R^2} t^2 \text{ meters}$$after $t$ seconds, where $G$ is a universal constant, $M$ is the moon's mass in kilograms, and $R$ is the moon's radius in meters. So if we know $G$, $M$, and $R$, then Newton's laws let us predict how far an object will fall over any amount of time.
To verify the accuracy of this law, we will calculate the difference between the predicted distance the hammer drops and the actual distance. (If they are different, it might be because Newton's laws are wrong, or because our measurements are imprecise, or because there are other factors affecting the hammer for which we haven't accounted.)
Someone studied the video and estimated that the hammer was dropped 113 cm from the surface. Counting frames in the video, the hammer falls for 1.2 seconds (36 frames).
Question 2.3.1. Complete the code in the next cell to fill in the data from the experiment.
Hint: No computation required; just fill in data from the paragraph above.
# time t, the duration of the fall in the experiment, in seconds.
# Replace the ellipsis ("...") in the line below with your
# estimate of the duration of the fall
time = ...
# The estimated distance the hammer actually fell, in meters.
# Replace the ellipsis ("...") in the line below with your
# estimate of the length of the fall
estimated_distance_m = ...
ok.grade("q2_3_1");
Question 2.3.2. Now, complete the code in the next cell to compute the difference between the predicted and estimated distances (in meters) that the hammer fell in this experiment.
This just means translating the formula above ($\frac{1}{2}G\frac{M}{R^2}t^2$) into Python code. You'll have to replace each variable in the math formula with the name we gave that number in Python code.
Hint: Try to use variables you've already defined in question 4.1.1
# First, we've written down the values of the 3 universal constants
# that show up in Newton's formula.
# G, the universal constant measuring the strength of gravity.
gravity_constant = 6.674 * 10**-11
# M, the moon's mass, in kilograms.
moon_mass_kg = 7.34767309 * 10**22
# R, the radius of the moon, in meters.
moon_radius_m = 1.737 * 10**6
# The distance the hammer should have fallen
# over the duration of the fall, in meters,
# according to Newton's law of gravity.
# The text above describes the formula
# for this distance given by Newton's law.
# **YOU FILL THIS PART IN.**
predicted_distance_m = ...
# Here we've computed the difference
# between the predicted fall distance and the distance we actually measured.
# If you've filled in the above code, this should just work.
difference = predicted_distance_m - estimated_distance_m
difference
ok.grade("q2_3_2");
2.4. Lists¶
Lists and their siblings, numpy arrays, are ordered collections of objects that have an order. Lists allow us to store groups of variables under one name. The order then allows us to access the objects in the list for easy access and analysis. If you want an in-depth look at the capabilities of lists, take a look at <https://www.tutorialspoint.com/python/python_lists.htm>
To initialize a list, you use brackets. Putting objects separated by commas in between the brackets will add them to the list. For example, we can create and name an empty list:
list_example = []
print(list_example)
We can add an object to the end of a list:
list_example = list_example + [5]
print(list_example)
Now we have a one-element list. And we can add another element:
list-example = list-example + [10]
to make a two-element list.
We can join "concatenate" two lists together:
list_example_two = list_example + [1, 3, 6, 'lists', 'are', 'fun', 4]
print(list_example_two)
/Digression: It is, I think, a mistake for python to use
+in this way. In arithmetic,+is simply addition. With lists,+smashes the two lists on either side together to make a bigger list. This can be a source of great confusion:
# overloading of the `+` operator considered harmful:
four = 4
print("this '4' is a number:", four, "; so '+' is addition and so", four, "+", four, "=", four + four)
four = [4]
print("this '4' is a list:", four, "; so '+' is list concatenation and so", four, "+", four, "=", four + four)
four = '4'
print("even worse is: this '4' is a string-of-symbols:", four, "; so '+' is symbol concatenation and so", four, "+", four, "=", four + four)
this '4' is a number: 4 ; so '+' is addition and so 4 + 4 = 8 this '4' is a list: [4] ; so '+' is list concatenation and so [4] + [4] = [4, 4] even worse is: this '4' is a string-of-symbols: 4 ; so '+' is symbol concatenation and so 4 + 4 = 44
which gives you no clue in the output as to why the result is different at all. /End Digression
To access not the list as a whole but an individual value in the list, simply count from the start of the list, and put the place of the object you want to access in brackets after the name of the list. But you have to start counting from not one but zero. Thus the initial object of a list has index 0, the second object of a list has index 1, and in the list above the eighth object has index 7:
selected_example = list_example_two[7]
print(selected_example)
Lists do not have to be made up of elements of the same kind. Indices do not have to be taken one at a time, either. Instead, we can take a slice of indices and return the elements at those indices as a separate list. Suppose we just want to select out items 4 through 6 from a list. We can do so:
selected_list = list_example_two[4:7]
print(selected_list)
We can select out the largest and smallest items of a list via min and max:
# A list containing six integers.
a_list = [1, 6, 4, 8, 13, 2]
# Another list containing six integers.
b_list = [4, 5, 2, 14, 9, 11]
print('Max of a_list:', max(a_list))
print('Min of b_list:', min(a_list))
Numpy arrays are siblings of lists that can be operated on arithmetically with much more versatility than regular lists. Let us start by making an array that consists of the numbers from zero to nine:
example_array = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
print(example_array)
This could have been accomplished more quickly:
example_array_2 = np.arange(10)
print('Undoubled Array: ', example_array_2)
Multiplying a list and an array by a number produce different results:
print('Multiplying a list by 2: ', 2 * b_list)
print('Multiplying an array by 2: ',2 * example_array_2)
3. Programming¶
3.1. Looping¶
Loops <https://www.tutorialspoint.com/python/python_loops.htm> are useful in manipulating, iterating over, or transforming large lists and arrays. The for loop is useful in that it travels through a list, performing an action at each element. The following code cell moves through every element in example_array, adds it to the previous element in example_array, and copies this sum to a new array.
new_list = []
for element in example_array:
new_element = element + 5
new_list.append(new_element)
print(new_list)
The most important line in the above cell is the "for element in..." line. This statement sets the structure of our loop, instructing the machine to stop at every number in example_array, perform the indicated operations, and then move on. Once Python has stopped at every element in example_array, the loop is completed and the final line, which outputs new_list, is executed.
Note that we did not have to use "element" to refer to whichever index value the loop is currently operating on. We could have called it almost anything. For example:
newer_list = []
for completely_arbitrary_name in example_array:
newer_element = completely_arbitrary_name + 5
newer_list.append(newer_element)
print(newer_list)
For loops can also iterate over ranges of numerical values. For example:
for i in range(len(example_array)):
example_array[i] = example_array[i] + 5
print(example_array)
The while loop repeatedly performs operations until a condition is no longer satisfied. Consider the example below. When the program enters the while loop, it notices that the maximum value of the while_array is less than 50. Because of this, it adds 1 to the fifth element, as instructed.
The program then goes back to the start of the loop. Again, the maximum value is less than 50. This process repeats until the the fifth element, now the maximum value of the array, is equal to 50, at which point the condition is no longer true, and the python interpreter moves on to the "print" command:
while_array = np.arange(10) # Generate our array of values
print('Before:', while_array)
while(max(while_array) < 50): # Set our conditional
while_array[4] += 1 # Add 1 to the fifth element if the conditional is satisfied
print('After:', while_array)
3.2. Functions¶
The most common way to combine or manipulate values in Python is by calling functions. Python comes with many built-in functions that perform common operations.
For example, the abs function takes a single number as its argument and returns the absolute value of that number. Run the next two cells and see if you understand the output.
abs(5)
abs(-5)
Example: computing walking distances: Chunhua is on the corner of 7th Avenue and 42nd Street in Midtown Manhattan, and she wants to know far she'd have to walk to get to Gramercy School on the corner of 10th Avenue and 34th Street.
She can't cut across blocks diagonally, since there are buildings in the way. She has to walk along the sidewalks. Using the map below, she sees she'd have to walk 3 avenues (long blocks) and 8 streets (short blocks). In terms of the given numbers, she computed 3 as the difference between 7 and 10, in absolute value, and 8 similarly.
Chunhua also knows that blocks in Manhattan are all about 80m by 274m (avenues are farther apart than streets). So in total, she'd have to walk $(80 \times |42 - 34| + 274 \times |7 - 10|)$ meters to get to the park.
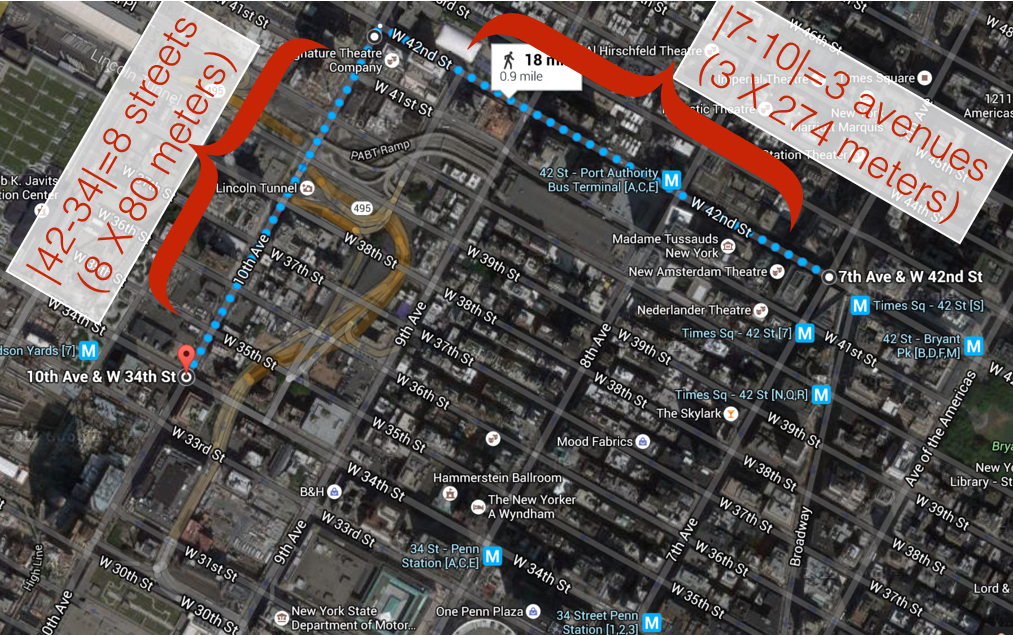
Question 3.2.1. Fill in the line num_avenues_away = ... in the next cell so that the cell calculates the distance Chunhua must walk and gives it the name manhattan_distance. Everything else has been filled in for you. Use the abs function. Also, be sure to run the test cell afterward to test your code.
# Here's the number of streets away:
num_streets_away = abs(42-34)
# Compute the number of avenues away in a similar way:
num_avenues_away = ...
street_length_m = 80
avenue_length_m = 274
# Now we compute the total distance Chunhua must walk.
manhattan_distance = street_length_m*num_streets_away + avenue_length_m*num_avenues_away
# We've included this line so that you see the distance you've computed
# when you run this cell.
# You don't need to change it, but you can if you want.
manhattan_distance
ok.grade("q3_2_1");
Multiple arguments: Some functions take multiple arguments, separated by commas. For example, the built-in max function returns the maximum argument passed to it.
max(2, -3, 4, -5)
3.3. Nested expressions¶
Function calls and arithmetic expressions can themselves contain expressions. You saw an example in the last question:
abs(42-34)
has 2 number expressions in a subtraction expression in a function call expression. And you probably wrote something like abs(7-10) to compute num_avenues_away.
Nested expressions can turn into complicated-looking code. However, the way in which complicated expressions break down is very regular.
Suppose we are interested in heights that are very unusual. We'll say that a height is unusual to the extent that it's far away on the number line from the average human height. An estimate of the average adult human height (averaging, we hope, over all humans on Earth today) is 1.688 meters.
So if Kayla is 1.21 meters tall, then her height is $|1.21 - 1.688|$, or $.478$, meters away from the average. Here's a picture of that:

And here's how we'd write that in one line of Python code:
abs(1.21 - 1.688)
What's going on here? abs takes just one argument, so the stuff inside the parentheses is all part of that single argument. Specifically, the argument is the value of the expression 1.21 - 1.688. The value of that expression is -.478. That value is the argument to abs. The absolute value of that is .478, so .478 is the value of the full expression abs(1.21 - 1.688).
Picture simplifying the expression in several steps:
abs(1.21 - 1.688)abs(-.478).478
In fact, that's basically what Python does to compute the value of the expression.
Question 3.3.1. Say that Paola's height is 1.76 meters. In the next cell, use abs to compute the absolute value of the difference between Paola's height and the average human height. Give that value the name paola_distance_from_average_m.

# Replace the ... with an expression
# to compute the absolute value
# of the difference between Paola's height (1.76m) and the average human height.
paola_distance_from_average_m = ...
# Again, we've written this here
# so that the distance you compute will get printed
# when you run this cell.
paola_distance_from_average_m
ok.grade("q3_3_1");
Now say that we want to compute the more unusual of the two heights. We'll use the function max, which (again) takes two numbers as arguments and returns the larger of the two arguments. Combining that with the abs function, we can compute the larger distance from average among the two heights:
# Just read and run this cell.
kayla_height_m = 1.21
paola_height_m = 1.76
average_adult_height_m = 1.688
# The larger distance from the average human height, among the two heights:
larger_distance_m = max(abs(kayla_height_m - average_adult_height_m), abs(paola_height_m - average_adult_height_m))
# Print out our results in a nice readable format:
print("The larger distance from the average height among these two people is", larger_distance_m, "meters.")
The line where larger_distance_m is computed looks complicated, but we can break it down into simpler components just like we did before.
The basic recipe is to repeatedly simplify small parts of the expression:
- Basic expressions: Start with expressions whose values we know, like names or numbers.
- Examples:
paola_height_mor5.
- Examples:
- Find the next simplest group of expressions: Look for basic expressions that are directly connected to each other. This can be by arithmetic or as arguments to a function call.
- Example:
kayla_height_m - average_adult_height_m.
- Example:
- Evaluate that group: Evaluate the arithmetic expression or function call. Use the value computed to replace the group of expressions.
- Example:
kayla_height_m - average_adult_height_mbecomes-.478.
- Example:
- Repeat: Continue this process, using the value of the previously-evaluated expression as a new basic expression. Stop when we've evaluated the entire expression.
- Example:
abs(-.478)becomes.478, andmax(.478, .072)becomes.478.
- Example:
You can run the next cell to see a slideshow of that process.
from IPython.display import IFrame
IFrame('https://docs.google.com/presentation/d/e/2PACX-1vTiIUOa9tP4pHPesrI8p2TCp8WCOJtTb3usOacQFPfkEfvQMmX-JYEW3OnBoTmQEJWAHdBP6Mvp053G/embed?start=false&loop=false&delayms=3000', 800, 600)
Ok, your turn:
Question 3.3.2. Given the heights of players from the Golden State Warriors, write an expression that computes the smallest difference between any of the three heights. Your expression shouldn't have any numbers in it, only function calls and the names klay, steph, and dangelo. Give the value of your expression the name min_height_difference.
# The three players' heights, in meters:
klay = 2.01 # Klay Thompson is 6'7"
steph = 1.91 # Steph Curry is 6'3"
dangelo = 1.95 # D'Angelo Russell is 6'5"
# We'd like to look at all 3 pairs of heights,
# compute the absolute difference between each pair,
# and then find the smallest of those 3 absolute differences.
# This is left to you!
# If you're stuck, try computing the value for each step of the process
# (like the difference between Klay's heigh and Steph's height)
# on a separate line and giving it a name (like klay_steph_height_diff)6
min_height_difference = ...
ok.grade("q3_3_2");
That brings us to the end of the "problem set" portion of this jupyter notebook. The next two sections are much more in the mode of a data-science lecture than an exercise. Follow along to get a taste of the kind of data manipulation and visualization we will be doing using three python extensions: the numerical python, python data analysis, and mathematical plotting libraries numpy, pandas, and matplotlib:
at_the_dawn = [-68000, 1, 1200, 0.1]
at_the_dawn
This list contains four elements:
- The first element in this list is an integer, the date by the current calendar: 70000 years ago is the year 68000 BCE, or 68000 BC, or -68000. (Back when Werner Rolevinck's Little Bundles of Time was published in Cologne Germany and became the best-selling book of the 1400s after the Bible, European intellectuals feared dn did not understand negative numbers: hence the "BC" and the counting backwards stuff. But we do understand negative numbers.)
- The second element is a real number ("real" in the sense of "not imaginary", i.e., not involving the square root of minus one), a number with a fractional or right-of-the-decimal-point part, my guess of the value of the stock of useful ideas about technology and organization that was then the common property of humanity.
- The third element is another real number, my guess of the average standard of living back then: about $1200 per capita per year (but relative prices were very different, so treat that number gingerly and with suspicion).
- The fourth element is yet another real number, the human population in millions: about 0.1—that is, there were perhaps only 100,000 people alive on the globe.
4.2. Python Data Analysis Library¶
One list by itself for the year -68000 is not very useful. It becomes useful only when we combine it with other lists in a larger set of data. But then we need infotech tools to work with groups of lists.
So back in 2008 computer programmer Wes McKinney began developing the Python Data Analysis Library—which he called Pandas (you can see where the "d" and the second "a" come from, but the first "a", the "n", and the "s"?). His bosses at AQR Capital Management up to and including Cliff Asness (with whom I have had some remarkable fights, on twitter and elsewhere) did a very good thing when they gave him the green light to open-source it. And because of its power, flexibility, and gentle learning curve pandas has since become the standard tool for data manipulation and data cleaning.
In order to invoke any pandas commands, you first need to call it from the vasty deep into your working environment. And because it is built on top of the Numerical Python Library, numpy, you need to call numpy into your environment as well. It is conventional to do it with the commands:
import numpy as np
import pandas as pd
Why the "import..."? Because you need to tell the python interpreter that the command you are looking for comes from the pandas (or numpy) library. "as np" and "as pd"? Because people got tired of typing "pandas" so many times in their code, and decided they would rather just type a quick "pd" instead.
4.3. Pandas dataframes¶
Think of a pandas dataframe as a table with rows and columns. The rows and columns of a pandas dataframe are best thought of as a collection of lists stacked on top/next to each other. For example, here is a collection—a list of lists—of eleven lists like our at the dawn list, each for a different date:
long_run_growth_list_of_lists = [
[-68000, 1, 1200, 0.1],
[-8000, 5, 1200, 2.5],
[-6000, 6.3, 900, 7],
[-3000, 9.2, 900, 15],
[-1000, 16.8, 900, 50],
[1, 30.9, 900, 170],
[800, 41.1, 900, 300],
[1500, 53, 900, 500],
[1770, 79.4, 1100, 750],
[1870, 123.5, 1300, 1300],
[2020, 2720.5, 11842, 7600]
]
You will notice that the final two meaningful symbols in the code cell above are "] ]". The first "]" markes the end of the 'whatever comes next' list for the python interpreter. The second and final "]" marks the end of the list-of-lists. That we have here a list with eleven elements, and that each element is itself a list, should bend your brain a little bit if you have not seen this kind of thing before. Get used to it. You will see a lot of such tail-chasing and tail-swallowing in modern information technologies.
The code cell above simply gives us a list with lists as its elements: it is not yet a pandas dataframe. Once we have imported the pandas library into our working environment, we can tell the python interpreter to turn it into a dataframe with the command to create the dataframe long_run_growth_df thus:
long_run_growth_df = pd.DataFrame(
data=np.array(long_run_growth_list_of_lists), columns = ['year', 'human_ideas', 'income_level', 'population']
)
long_run_growth_df
4.4. A few good programming practices...¶
As before, when the last line of the code cell is simply the name of some object, the python interpreter understands that to be a request that it evaluate that object and print it out. And we see that we have indeed created the data table we had hoped to construct.
We have called it "long_run_growth" to remind us that it is made up of data about the long run growth of the human economy, and we have the "_df" at the end to remind us that it is a pandas dataframe. Note the "pd." in front of "DataFrame" to tell the python interpreter that the command comes from pandas. Note the "np." in front of "array" to tell the python interpreter that we want it to look into the numpy, the Numerical Python, library for the array command to apply to long_run_growth_list_of_lists. And note the ", columns = " to tell the python interpreter that it should label each of the columns of the dataframe, and what those labels should be.
4.5. Cleaning the dataset¶
Now we need to do a little housecleaning:
# first, see what the python interpreter thinks our "year" column is:
long_run_growth_df['year']
# make sure that the python interpreter understands that
# the year is an integer—that is, a number without any
# fractional after-the-decimal-point part:
long_run_growth_df['year'] = long_run_growth_df['year'].apply(np.int64)
long_run_growth_df['year']
Yes! Before the python interpreter had thought that the "year" column was a real number (i.e., not an imaginary number: not a number related to the square root of minus one) with a fractional after-the-decimal-point-part. Before it had set up the "year" column as a column in which each element was a 52 binary digits ("bit")-precise number in which where the decimal point was "floated" depending on the value of an 11-bit exponent, which plus an extra bit to tell whether the number was positive or negative. Now the python interpreter knows that year is an integer.
# make a new variable which is simply the year at which each
# of the ten periods into which our dataframe divides human
# history is taken to start:
long_run_growth_df['initial_year'] = long_run_growth_df['year']
initial_year = long_run_growth_df['initial_year'][0:10]
initial_year
(Parenthetically, is is almost always good to end each code cell with the name of the object the cell asks the python interpreter to calculate. Then you can look at what the python interpreter evaluates the object to be—in this case, a ten-element pandas series list called "year" each element of which is a 64-bit integer number—to check that the computer is doing what you expected and wanted it to do.
# now we calculate era lengths—which we call "span"—and also
# calculate the growth rates, over our different eras, g for
# the proportional growth rate of real income per capita (and
# also of the efficiency of labor), n for the proportional
# rate of growth of the human population, & h for the
# proportional growth rate of the value of useful human
# ideas about technology and organization h:
span = []
g = []
h = []
n = []
for t in range(10):
span = span +[long_run_growth_df['year'][t+1]-long_run_growth_df['year'][t]]
h = h + [np.log(long_run_growth_df['human_ideas'][t+1]/long_run_growth_df['human_ideas'][t])/span[t]]
g = g + [np.log(long_run_growth_df['income_level'][t+1]/long_run_growth_df['income_level'][t])/span[t]]
n = n + [np.log(long_run_growth_df['population'][t+1]/long_run_growth_df['population'][t])/span[t]]
n
Here we see that $ n $—the human population proportional growth rate for the ten eras -68000 to -8000, -8000 to -6000, -6000 to -3000, -3000 to -1000, -1000 to 1, 1 to 800, 800-1500, 1500-1770, 1770-1870, and 1870-2020—is a ten element python list, which is what we hoped it would be, and that its last element, 0,0117718..., is in fact the annual average proprtional growth rate of the human population over the modern economic growth era from 1870 to 2020, during which humanity's population grew from 1.3 to 7.6 billion.
# next, we tell the python interpreter that these data
# are naturally indexed by the year:
long_run_growth_df.set_index('year', inplace=True)
# &, last, we check to make sure that nothing has gone wrong
# yet with our computations. we check to see that we can
# refer to columns of the datafrme by the labels we assigned
# to them & that the python interpreter understands that the year
# to which each observation corresponds is its natural index:
long_run_growth_df['income_level']
# remember those growth rates we calculated? we can stuff them
# into their own dataframe and take a look:
long_run_growth_rates_df = pd.DataFrame(
data=np.array([initial_year, span, h, g, n]).transpose(),
columns = ['initial_year', 'span', 'h', 'g', 'n'])
long_run_growth_rates_df['initial_year'] = long_run_growth_rates_df['initial_year'].apply(np.int64)
long_run_growth_rates_df.set_index('initial_year', inplace=True)
long_run_growth_rates_df
And, last, to make it easier to understand what we have done, let us label the eras into which we have divided human history:
eras = ['at the dawn', 'agriculture & herding', 'proto-agrarian age',
'writing', 'axial age', 'late-antiquity pause', 'middle age', 'commercial revolution',
'industrial revolution', 'modern economic growth', 'what the 21st century brings']
long_run_growth_df['eras'] = eras
eras = eras[0:10]
long_run_growth_rates_df['eras'] = eras
long_run_growth_rates_df
Most of the work involved in being an analyst involves this kind of "data cleaning" exercise. It is boring. It is remarkably difficult, and time consuming:

It is essential to get right, or you will fall victim to the programming saying: garbage in, garbage out. And it is essential to do so in a way that leaves a trail that even a huge idiot can follow should one in the future attempt to understand what you have done to create the dataset you are analyzing—and there is no bigger idiot who needs a lot of help to understand where the dataset came from and what it is than yourself next year, or next month, or next week, or tomorrow.
This is why we jump through all these hoops: so that somebody coming across this notebook file one or five or ten years from now will not be hopelessly lost in trying to figure out what is supposed to be going on here.
To make the tasks of whoever may look at this in the future—which may well be you—I recommend an additional data cleaning step. Take the name of your dataframe, replace the "_df" at its end with "_dict", thus creating what python calls a dictionary object, then stuff the dataframe into the dictionary, and finally add information about the sources of the data:
long_run_growth_dict = {}
long_run_growth_dict['dataframe'] = long_run_growth_df
long_run_growth_dict['source'] = 'Brad DeLong\'s guesses about the shape of long-run human economic history'
long_run_growth_dict['source_date'] = '2020-05-24'
If you follow this convention, then anyone running across one of your dataframes in the future will be able to quickly get up to speed on where the data came from by simply typing:
long_run_growth_dict['source']
4.6. The psychology of programming¶
Do you feel bewildered? As if I have been issuing incomprehensible and arcane commands to some deep and mysterious entities that may or may not respond in the expected way? All who program feel this way some of the time, and most of those who program feel this way most of the time. For example, consider the URL you typed to get to this notebook. It was the arcane: <http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=lecture-support-2020&branch=master&path=ps00.ipynb> which accessed the ps00.ipynb file in the master branch of my lecture-support-2020 repository of files on the <http://github.com/> website, which is in the ingenious and powerful git format. But I have never met anybody able and willing to explain how git works to me, and I do not think cartoonist Randall Munroe has met anyone either. It is all just magic:

https://imgs.xkcd.com/comics/git.png
And at times you are sure to feel worse than bewildered. You will feel like python newbee Gandalf feels at this moment:

This "sorcerer's apprentice" <https://www.youtube.com/watch?v=2DX2yVucz24> feeling is remarkably common among programmers. It is explicitly referenced in the introduction to the classic computer science textbook, Abelson, Sussman, & Sussman: Structure and Interpretation of Computer Programs <https://github.com/braddelong/public-files/blob/master/readings/book-abelson-structure.pdf>:
In effect, we conjure the spirits of the computer with our spells.
A computational process is indeed much like a sorcerer’s idea of a spirit. It cannot be seen or touched. It is not composed of matter at all. However, it is very real. It can perform intellectual work. It can answer questions. It can affect the world by disbursing money at a bank or by controlling a robot arm in a factory. The programs we use to conjure processes are like a sorcerer’s spells. They are carefully composed from symbolic expressions in arcane and esoteric programming languages that prescribe the tasks we want our processes to perform. A computational process, in a correctly working computer, executes programs precisely and accurately. Thus, like the sorcerer’s apprentice, novice programmers must learn to understand and to anticipate the consequences of their conjuring.... Master software engineers have the ability to organize programs so that they can be reasonably sure that the resulting processes will perform the tasks intended...
4.7. Comment your code!¶
You may recall these lines in the cell in which you answered Question 1.2.1:
# Change the next line
# so that it computes the number of seconds in a decade
# and assigns that number the name, seconds_in_a_decade.
This is called a comment. It doesn't make anything happen in Python; Python ignores anything on a line after a #. Instead, it's there to communicate something about the code to you, the human reader. Comments are extremely useful.

Source: http://imgs.xkcd.com/comics/future_self.png
Why are comments useful? Because anyone who will read and try to understand your code in the future is guaranteed to be an idiot. You need to explain things to them very simply, as if they were a small child.
They are not really an idiot, of course. It is just that they are not in-the-moment, and do not have the context in their minds that you have when you write your code.
And always keep in mind that the biggest idiot of all is also the one who will be most desperate to understand what you have written: it is yourself, a month or more from now, especially near th eend of the semester.
4.8. Maintain your machines¶
These assignments will be very difficult to do on a smartphone.
Understand and keep your laptop running—or understand, keep running, and get really really good at using your tablet. Machines do not need to be expensive: around 150 dollars should do it for a Chromebook. People I know like the Samsung Exynos 5 <https://www.amazon.com/Samsung-Chromebook-Exynos-Dual-Core-XE303C12-A01US/dp/B01LXJZWVF/> or the Lenovo 3 11" <https://www.walmart.com/ip/11-Drive-82BA0000US-Processor-RAM-Celeron-Black-Intel-Solid-Chromebook-4GB-Display-Chrome-4GB-32GB-Lenovo-OS-Dual-Core-N4020-32GB-eMMC-3-11-6-State-O/402347782>.
And have a backup plan: what will you do if your machine breaks and has to go into the shop, or gets stolen?
4.9. Why jump through all these hoops here?¶
You may feel that we have gone through a lot of extra and unnecessary work to create this dataframe. If you are familiar with a spreadsheet program like Microsoft Excel, you may wonder why we don't just use a spreadsheet to hold and then do calculations with the data in this small table that is long_run_growth_df. Indeed, Bob Frankston and Dan Bricklin who implemented and designed the original Visicalc were geniuses. Visicalc was a tremendously useful advance over earlier mainframe-based report generators, such as ITS's Business Planning Language <https://en.wikipedia.org/wiki/VisiCalc>. And today's Microsoft Excel is not that great an advance over Jonathan Sachs's Lotus 1-2-3, which was itself close to being merely a knockoff of Visicalc. Why not follow the line of least resistance? Why not do our data analysis and visualization in a spreadsheet?
I do not recommend using spreadsheet programs. In fact, I greatly disrecommend using spreadsheet programs.
Why?
This is why:

If you do your work in a spreadsheet, and it rapidly becomes impossible to check or understand. A spreadsheet is a uniquely easy framework to work in. A spreadsheet is a uniquely opaque and incomprehensible framework to assess for its correctness.
Since we all make errors, frequently, the ability to look back and assess whether one's calculations are correct is absolutely essential. With spreadsheets, such checking is impossible. And sooner or later with very high probability you will make a large and consequential mistake that you will not catch.
4.10. Selecting and sorting information¶
From our long_run_growth_rates_df dataframe, suppose we wanted to select only those eras in which the average rate of human population growth was less than a quarter of a percent per year. We would do so by:
long_run_growth_rates_df[long_run_growth_rates_df['n'] < 0.001]
We find seven such eras. If we wanted to look at only the rates of growth of income per capita in those eras, we would write:
long_run_growth_rates_df[long_run_growth_rates_df['n'] < 0.001]['g']
From our long_run_growth_df dataframe, suppose we wanted to sort the rows of the dataframe in decreasing order of how rich humanity was at each point. We would then write:
long_run_growth_df.sort_values("income_level", ascending=False)
We see that humanity has recently been richer—very recently very richer—than ever before. But we also see that there was a long stretch of history, from the year -6000 up to 1770, when humanity was poorer than it had been before in the industrial revolution era.
Suppose we wanted to just look at data before the year 1:
long_run_growth_df[long_run_growth_df['initial_year'] < 1]
Or suppose we just wanted to look at income level and population data after 1500:
long_run_growth_df[long_run_growth_df['initial_year'] > 1500][['income_level', 'population']]
Or suppose we to look at the population for the year 1500:
long_run_growth_df['population'][1500]
And if we want to write our dataframes to "disk"—a word we still use because for a generation computer data could be stored in one of three places: in the computer's volatile memory where it disappeared when the power went off or when the computer crashed; on spinning disks with little magnets on them; or archived, offsite, on reels of tape. Why would we want to do so? So that we can easily reuse the data someplace else, or find it again later.
Pandas attaches methods to its dataframe to make this easy:
# write our two dataframes to "disk"
long_run_growth_df.to_csv('long_run_growth.csv')
long_run_growth_rates_df.to_csv('long_run_growth_rates.csv')
where ".csv" tells the python interpreter that the data is in the form of comma-separated values, so that you can actually read it and understand it with your eyes if necessary.
4.11. Reading in dataframes¶
Luckily for you, all of this data cleaning above will be largely irrelevant for this course. Almost all datatables in this course will be premade and given to you in a form that is easily read into a pandas method, which creates the table for you.
A common file type that is used for economic data is a comma-separated Values (.csv) file. If you know the url or the file name and location (the "file path"), you use the "read_csv" method from pandas, which requires one single parameter: the path to the csv file you are reading in.
# run this cell to read in the datatables and set the
# indexes:
long_run_growth_df = pd.read_csv("https://delong.typepad.com/files/long_run_growth.csv")
long_run_growth_rates_df = pd.read_csv("https://delong.typepad.com/files/long_run_growth_rates.csv")
long_run_growth_df.set_index('year', inplace=True)
long_run_growth_rates_df.set_index('initial_year', inplace=True)
long_run_growth_df
Load in the data using pd.read_csv(), set your indices using name_df.set_index(), and you are ready to go with your data analysis with no required or needed data cleaning at all.
5. Visualization ¶
Now that you can read in data and manipulate it, you are now ready to learn about how to visualize data. To begin, run the cell below to import the required libraries, to make graphs appear inside the notebook rather than in a separate window, and to load and set the indexes for the dataframes:
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
long_run_growth_df = pd.read_csv("https://delong.typepad.com/files/long_run_growth.csv")
long_run_growth_rates_df = pd.read_csv("https://delong.typepad.com/files/long_run_growth_rates.csv")
long_run_growth_df.set_index('year', inplace=True)
long_run_growth_rates_df.set_index('initial_year', inplace=True)
Check to make sure that the long_run_growth_df is what it was supposed to be:
long_run_growth_df
Check to make sure that the long_run_growth_rates_df is what it was supposed to be:
long_run_growth_rates_df
and we are ready to roll...
5.1. It is very easy¶
There is very little left to do in order to visualize our data.
5.2. The most eagle's eye view¶
To graph how wealth per capita has evolved over human history, we simply write:
long_run_growth_df['income_level'].plot()
That is it.
One of the treat advantages of python and pandas is its built-in plotting methods. We can simply call .plot() on a dataframe to plot columns against one another. All that we have to do is specify which column to plot on which axis. Something special that pandas does is attempt to automatically parse dates into something that it can understand and order them sequentially.
We probably want to pretty-up the graph a little bit, adding labels:
long_run_growth_df['income_level'].plot()
plt.title('Human Economic History: Wealth per Capita', size=20)
plt.xlabel('Year')
plt.ylabel('Annual Income per Capita, 2020 Dollars')
Freaky, no?
This is why U.C. Davis economic historian Greg Clark says that there is really only one graph that is important in economic history.
How do the other variables in our dataframe look?
long_run_growth_df['population'].plot()
plt.title('Human Economic History: Population', size=20)
plt.xlabel('Year')
plt.ylabel('Millions')
long_run_growth_df['human_ideas'].plot()
plt.title('Human Economic History: Ideas', size=20)
plt.xlabel('Year')
plt.ylabel('Index of Useful Ideas Stock')
5.3. Looking at logarithmic scales¶
After the spring of coronavirus, we are used to exponential growth processes—things that explode, but only after a time in which they gather force, and which look like straight line growth on a graph plotted on a logarithmic scale. Let us plot income levels, populations, and ideas stock values on log scales and see what we see:
np.log(long_run_growth_df['income_level']).plot()
plt.title('Human Economic History: Wealth', size=20)
plt.xlabel('Year')
plt.ylabel('Log Annual Income per Capita, 2020 Dollars')
np.log(long_run_growth_df['population']).plot()
plt.title('Human Economic History: Population', size=20)
plt.xlabel('Year')
plt.ylabel('Log Millions')
np.log(long_run_growth_df['human_ideas']).plot()
plt.title('Human Economic History: Ideas', size=20)
plt.xlabel('Year')
plt.ylabel('Log Index of Useful Ideas Stock')
5.4. Slicing the data to look at subsamples¶
What we have here is not an exponential growth process—at least, not recently, for very large values of "recently". But perhaps we really do not care about what went on in the gatherer-hunter age before 10,000 years ago, or even in the early agrarian age before 5000 years ago. We know how to take slices out of a dataframe. And with Python those slices then act like dataframes too. So we can simply use the plot() method to look at subsamples:
long_run_growth_df['income_level'][3:].plot()
Still definitely not an exponential...
Insert some code cells below, and in them run some plot commands both to pretty-up your figures with labels and to examine how the time series behave over the past five thousand years, roughly since the invention of writing.
Suppose you want to gain a sense of how the variables behaved back in the long agrarian age, after the gatherer-hunter age but before the Industrial Revolution that started in 1770. Then we once again use the same commands we used for lists to slice the dataframe:
long_run_growth_df['income_level'][1:9].plot()
plt.title('Human Economic History: Wealth', size=20)
plt.xlabel('Year')
plt.ylabel('Annual Income per Capita, 2020 Dollars')
long_run_growth_df['population'][1:9].plot()
plt.title('Human Economic History: Population', size=20)
plt.xlabel('Year')
plt.ylabel('Millions')
long_run_growth_df['human_ideas'][1:9].plot()
plt.title('Human Economic History: Ideas', size=20)
plt.xlabel('Year')
plt.ylabel('Index of Useful Ideas Stock')
5.5. More attractive tables¶
When we simply print out our dataframe for growth rates across eras, it is relatively unattractive and hard to read:
long_run_growth_rates_df
Here making the printing prettier really matters—for us humans, at least, as we try to read what is going on.
We can make the printing prettier by defining a format dictionary format_dict (or whatever other name we choose) and feeding it to the dataframe, telling the dataframe that we want it to evaluate itself using its .style method, and that style() should use its .format() submethod to understand what the format_dict is asking the python interpreter to do:
format_dict = { 'span': '{0:.0f}', 'h': '{0:,.3%}',
'g': '{0:,.2%}', 'n': '{0:,.2%}'}
long_run_growth_rates_df.style.format(format_dict)
This is a much more human-readable presentation of the dataframe of calculated growth rates of the ideas stock, living standards of the typical human, and of the human population over the eras that make up human history...
6. You are done!¶
You're done with Problem set 0! Be sure to run the tests and verify that they all pass, then choose Save and Checkpoint from the File menu, then run the final cell to submit your work. If you submit multiple times, your last submission will be counted.
Important. In order to get credit, you need to run the final code cell below to submit your work:
# this cell is commented out;
# _ = ok.submit()
Thanks to Umar Maniku, Eric van Dusen, Anaise Jean-Philippe, Marc Dordal i Carrerras, & others for helpful comments. Very substantial elements of this were borrowed from the Berkeley Data 8 <http://data8.org> teaching materials, specifically Lab 01: https://github.com/data-8/materials-sp20/blob/master/materials/sp20/lab/lab01/lab01.ipynb>
Note: datahub link: <http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=lecture-support-2020&branch=master&path=ps00.ipynb>