Prelude¶
In this notebook, we provide a set of exercises that should help you prepare for the exam. There are two sets of exercises:
- (5SSB0). The first set contains questions from previous exams of class 5SSB0 (Adaptive Information Processing). 5SSB0 was last taught at TU/e in the academic year 2018/19. Starting with the academic year 2019/20, the current class (5SSD0) is offered instead. In comparison to 5SSB0, the emphasis of the current class is more on the Bayesian framework, rather than maximum likelihood. Below, we present a selection of exercises that were used in the 5SSB0 exams. While these exercises may not represent the emphasis on Bayesian methods, they do represent the "style of questions" and the "level of difficulty" that you may expect in upcoming 5SSD0 exams. Also, there is nothing in the questions below that is considered outside the scope of 5SSD0.
- (Rehearsal). A second set of exercises are categorized by lesson headers, e.g., "Probability Theory" or "Generative Classification". These exercises intend to test you on the contents of the corresponding lesson. Of course, for some exercises you may need some contents of some other (usually earlier) lessons or background materials. A perfect categorization is not feasible, but we've tried to link each question to a lesson so as to make it easier to test yourself after studying a specific lesson.
For some of these exercises you will be able to find solutions quickly on the internet. Try to resist this route to solving the problems. You will not be graded for these exercises and solutions will be made available in a separate notebook. Your ability to solve these exercises without external help provides an excellent indicator of your readiness to pass the exam.
This notebook is still under construction. We will be adding more exercises to help you prepare. Also, not all solutions are provided yet. We are working on this too. If you absolutely need the solution for a problem that doesn't have a solution yet, please contact one of the TAs (see http://bmlip.nl for contact info.)
As 2019/20 is the first time we teach this class, please be alert to errors (and let us know if you find any!) or more generally, let us know if things are unclear to you or if a question can be improved.
We are aware there are some rendering problems in some browsers. We are trying to fix that as well.
Good luck!
Cheatsheet¶
You are not allowed to bring books or notes to the exam. Instead, feel free to make use of the following cheatsheet as we will provide this or a similar cheatsheet in an appendix of the exam papers.
Some Matrix Calculus, see also Bishop, appendix C.
- Definition of the Multivariate Gaussian Distribution (MVG)
- A linear transformation $z=Ax+b$ of a Gaussian variable $\mathcal{N}(x|\mu,\Sigma)$ is Gaussian distributed as
- Multiplication of 2 Gaussian distributions
with $$\begin{align*} \Sigma_c^{-1} &= \Sigma_a^{-1} + \Sigma_b^{-1} \\ \Sigma_c^{-1}\mu_c &= \Sigma_a^{-1}\mu_a + \Sigma_b^{-1}\mu_b \\ \alpha &= \mathcal{N}(\mu_a | \mu_b, \Sigma_a + \Sigma_b) \end{align*}$$
- Conditioning and marginalization of Gaussians. Let $z = \begin{bmatrix} x \\ y \end{bmatrix}$ be jointly normal distributed as
then $p(z) = p(y|x)\cdot p(x)$, with $$\begin{align*} p(y|x) &= \mathcal{N}\left(y\,|\,\mu_y + \Sigma_{yx}\Sigma_x^{-1}(x-\mu_x),\, \Sigma_y - \Sigma_{yx}\Sigma_x^{-1}\Sigma_{xy} \right) \\ p(x) &= \mathcal{N}\left( x\,|\,\mu_x, \Sigma_x \right) \end{align*}$$
- For a binary variable $x \in \{0,1\}$, the Bernoulli distribution is given by
- The conjugate prior for $\mu$ is the Beta distribution, given by
where $\alpha$ and $\beta$ are "hyperparameters" that you can set to reflect your prior beliefs about $\mu$.
Selected exercises from previous exams "5SSB0"¶
[1] Answer shortly (max. 3 sentences): What is the difference between supervised and unsupervised learning?
[2] Which of the following statements is true (or justified)?
(a) If $X$ and $Y$ are independent Gaussian distributed variables, then $Z = 3X+Y$ is also a Gaussian distributed variable.
(b) The sum of two Gaussian functions is always also a Gaussian function.
(c) Discriminative classification is more similar to regression than to density estimation.
(d) Density estimation is more similar to generative classification than to discriminative classification.
(e) Clustering is more similar to supervised classification than to unsupervised classification.[3] Consider a binary classification problem with two classes $\{y_1,y_2\}$ and input vector $x$. Outputs $y_k$ are recorded by a one-hot encoding scheme. We are given a data set to train the parameters $\theta$ for a likelihood model of the form
There a two fundamentally different ways to train $\theta$, namely through a generative model or by discriminative training.
(a) Explain shortly how we train $\theta$ through a generative model. No need to work out all equations for Gaussian models, but explain the strategy in probabilistic modeling terms.
(b) Explain shortly how we train $\theta$ through a discriminative
approach.
[4] What is the difference between supervised and unsupervised learning? Express the goals of these two learning methods in terms of a probability distribution. (I'm looking here for a statement such as: " Given $\ldots$, the goals of supervised/unsupervised learning is to estimate $p(\cdot|\cdot)$".)
[5] In a particular model with hidden variables, the log-likelihood can be worked out to the following expression:
Do you prefer a gradient descent or EM algorithm to estimate maximum likelihood values for the parameters? Explain your answer. (No need to work out the equations.)
- [6] Consider a data set $D = \{x_1,x_2,\ldots,x_N\}$ where we assume that each sample $x_n$ is IID distributed by a multivariate Gaussian (MVG) $\mathcal{N}(x_n|\,\mu,\Sigma)$.
Proof that the maximum likelihood estimate (MLE) of the mean value of this distribution is given by $$\begin{equation*} \hat \mu = \frac{1}{N}\sum_n x_n \end{equation*}$$ (Note the list of matrix calculus formulas above).
- [7] Consider a data set $D = \{(x_1,y_1), (x_2,y_2),\dots,(x_N,y_N)\}$ with 1-of-$K$ notation for the discrete classes, i.e.,
together with class-conditional distribution $p(x_n| y_{nk}=1,\theta) = \mathcal{N}(x_n|\mu_k,\Sigma)$ and multinomial prior $p(y_{nk}=1) = \pi_k$.
(a) Proof that the joint log-likelihood is given by
$$\begin{equation*}
\log p(D|\theta) = \sum_{n,k} y_{nk} \log \mathcal{N}(x_n|\mu_k,\Sigma) + \sum_{n,k} y_{nk} \log \pi_k
\end{equation*}$$
(b) Show now that the MLE of the class-conditional mean is given by
$$\begin{equation*}
\hat \mu_k = \frac{\sum_n y_{nk} x_n}{\sum_n y_{nk}}
\end{equation*}
$$
[8] Consider an IID data set $D=\{(x_1,y_1),\ldots,(x_N,y_N)\}$. We will model this data set by a model $$y_n =\theta^T f(x_n) + e_n\,,$$ where $f(x_n)$ is an $M$-dimensional feature vector of input $x_n$; $y_n$ is a scalar output and $e_n \sim \mathcal{N}(0,\sigma^2)$.
(a) Rewrite the model in matrix form by lumping input features in a matrix $F=[f(x_1),\ldots,f(x_N)]^T$, outputs and noise in the vectors $y=[y_1,\ldots,y_N]^T$ and $e=[e_1,\ldots,e_N]^T$, respectively.(b) Now derive an expression for the log-likelihood $\log p(y|\,F,\theta,\sigma^2)$.
(c) Proof that the maximum likelihood estimate for the parameters is given by
(Note the list of matrix calculus formulas above).
(d) What is the predicted output value $y_\bullet$, given an observation $x_\bullet$ and the maximum likelihood parameters $\hat \theta_{\text{ml}}$. Work this expression out in terms of $F$, $y$ and $f(x_\bullet)$.
(e) Suppose that, before the data set $D$ was observed, we had reason to assume a prior distribution $p(\theta)=\mathcal{N}(0,\sigma_0^2)$. Derive the Maximum a posteriori (MAP) estimate $\hat \theta_{\text{map}}$.(hint: work this out in the $\log$ domain.)
- [9] For each of the following sub-questions, provide a short but essential answer.
(a) The joint distribution for feature vector $x$ and membership of $k$th class is given by (we use one-hot encoding of classes)
Write down an expression for the posterior class probability $p(y_k=1|x)$ (No derivations are needed, just a proper expression)?
(b) Why does maximum likelihood estimation become a better approximation to Bayesian learning as you collect more data?
(c) Given is a model $$\begin{align*} p(x|z) &= \mathcal{N}(x | W z,\Psi) \\ p(z) &= \mathcal{N}(z|0,I) \end{align*}$$ Work out an expression for the marginal distribution $p(x)$.
[10] Explain shortly how Bayes rule relates to machine learning in the context of an observed data set $D$ and a model $M$ with parameters $\theta$. Your answer must contain the expression for Bayes rule.
[11] Consider the following state-space model:
where $k=1,2,\ldots,n$ is the time step counter; $z_k$ is an unobserved state sequence; $x_k$ is an observed sequence; $w_k \sim \mathcal{N}(0,\Sigma_w)$ and $v_k \sim \mathcal{N}(0,\Sigma_v)$ are (unobserved) state and observation noise sequences respectively; $z_0 \sim \mathcal{N}(0,\Sigma_0)$ is the initial state and $A$, $C$, $\Sigma_v$,$\Sigma_w$ and $\Sigma_0$ are known parameters. The Forney-style factor graph (FFG) for one time step is depicted here:
 (a) Rewrite the state-space equations as a set of conditional probability distributions.
$$\begin{align*}
p(z_k|z_{k-1},A,\Sigma_w) &= \ldots \\
p(x_k|z_k,C,\Sigma_v) &= \ldots \\
p(z_0|\Sigma_0) &= \ldots
\end{align*}$$
(b) Define $z^n \triangleq (z_0,z_1,\ldots,z_n)$, $x^n \triangleq (x_1,\ldots,x_n)$ and $\theta=\{A,C,\Sigma_w,\Sigma_v\}$. Now write out the generative model $p(x^n,z^n|\theta)$ as a product of factors.
(c) We are interested in estimating $z_k$ from a given estimate for $z_{k-1}$ and the current observation $x_k$, i.e., we are interested in computing $p(z_k|z_{k-1},x_k,\theta)$. Can $p(z_k|z_{k-1},x_k,\theta)$ be expressed as a Gaussian distribution? Explain why or why not in one sentence.
(d) Copy the graph onto your exam paper and draw the message passing schedule for computing $p(z_k|z_{k-1},x_k,\theta)$ by drawing arrows in the factor graph. Indicate the order of the messages by assigning numbers to the arrows.
(e) Now assume that our belief about parameter $\Sigma_v$ is instead given by a distribution $p(\Sigma_v)$ (rather than a known value). Adapt the factor graph drawing of the previous answer to reflects our belief about $\Sigma_v$.
(a) Rewrite the state-space equations as a set of conditional probability distributions.
$$\begin{align*}
p(z_k|z_{k-1},A,\Sigma_w) &= \ldots \\
p(x_k|z_k,C,\Sigma_v) &= \ldots \\
p(z_0|\Sigma_0) &= \ldots
\end{align*}$$
(b) Define $z^n \triangleq (z_0,z_1,\ldots,z_n)$, $x^n \triangleq (x_1,\ldots,x_n)$ and $\theta=\{A,C,\Sigma_w,\Sigma_v\}$. Now write out the generative model $p(x^n,z^n|\theta)$ as a product of factors.
(c) We are interested in estimating $z_k$ from a given estimate for $z_{k-1}$ and the current observation $x_k$, i.e., we are interested in computing $p(z_k|z_{k-1},x_k,\theta)$. Can $p(z_k|z_{k-1},x_k,\theta)$ be expressed as a Gaussian distribution? Explain why or why not in one sentence.
(d) Copy the graph onto your exam paper and draw the message passing schedule for computing $p(z_k|z_{k-1},x_k,\theta)$ by drawing arrows in the factor graph. Indicate the order of the messages by assigning numbers to the arrows.
(e) Now assume that our belief about parameter $\Sigma_v$ is instead given by a distribution $p(\Sigma_v)$ (rather than a known value). Adapt the factor graph drawing of the previous answer to reflects our belief about $\Sigma_v$.
Rehearsal Exercises¶
- Below you will find more questions that test your knowledge of each lesson. My perception of the difficulty level of each question may differ from yours, but I ll indicate my ratings with three levels, (#) for easy, (##) for intermediate level and (###) for (very) challenging. While all questions are in principle within the scope of the lessons, there should be enough questions of levels (#) and (##) in the exams to pass the class.
Machine Learning Overview¶
- [1] (##) Pick three applications from the "Some Machine Learning Applications"-slide and (shortly) describe for each application how (a combination of) clustering, dimensionality reduction, regression classification or reinforcement learning could accomplish the task.
Probability Theory Review¶
- [1] (a) (#) Proof that the "elementary" sum rule $p(A) + p(\bar{A}) = 1$ follows from the (general) sum rule $$p(A+B) = p(A) + p(B) - p(A,B)\,.$$
(b) (###) Conversely, derive the general sum rule $p(A + B) = p(A) + p(B) - p(A,B)$
from the elementary sum rule $p(A) + p(\bar A) = 1$ and the product rule. Here, you may make use of the (Boolean logic) fact that $A + B = \overline {\bar A \bar B }$.
[2] Box 1 contains 8 apples and 4 oranges. Box 2 contains 10 apples and 2 oranges. Boxes are chosen with equal probability.
(a) (#) What is the probability of choosing an apple?
(b) (##) If an apple is chosen, what is the probability that it came from box 1?[3] (###) The inhabitants of an island tell the truth one third of the time. They lie with probability $2/3$. On an occasion, after one of them made a statement, you ask another "was that statement true?" and he says "yes". What is the probability that the statement was indeed true?
[4] (##) A bag contains one ball, known to be either white or black. A white ball is put in, the bag is shaken, and a ball is drawn out, which proves to be white. What is now the chance of drawing a white ball? (Note that the state of the bag, after the operations, is exactly identical to its state before.)
[5] A dark bag contains five red balls and seven green ones.
(a) (#) What is the probability of drawing a red ball on the first draw?
(b) (##) Balls are not returned to the bag after each draw. If you know that on the second draw the ball was a green one, what is now the probability of drawing a red ball on the first draw?[6] (#) Is it more correct to speak about the likelihood of a model (or model parameters) than about the likelihood of an observed data set. And why?
[7] (##) Is a speech signal a 'probabilistic' (random) or a deterministic signal?
[8] (##) Proof that, for any distribution of $x$ and $y$ and $z=x+y$
You may make use of the more general theorem that the mean and variance of any distribution $p(x)$ is processed by a linear tranformation as $$\begin{align*} \mathrm{E}[Ax +b] &= A\mathrm{E}[x] + b \\ \mathrm{var}[Ax +b] &= A\,\mathrm{var}[x]\,A^T \end{align*}$$
Bayesian Machine Learning¶
[1] (#) (a) Explain shortly the relation between machine learning and Bayes rule.
(b) How are Maximum a Posteriori (MAP) and Maximum Likelihood (ML) estimation related to Bayes rule and machine learning?[2] (#) What are the four stages of the Bayesian design approach?
[3] (##) The Bayes estimate is a summary of a posterior distribution by a delta distribution on its mean, i.e.,
Proof that the Bayes estimate minimizes the expected mean-square error, i.e., proof that $$ \hat \theta_{bayes} = \arg\min_{\hat \theta} \int_\theta (\hat \theta -\theta)^2 p \left( \theta |D \right) \,\mathrm{d}{\theta} $$
- [4] (##) We make $N$ IID observations $D=\{x_1 \dots x_N\}$ and assume the following model
where $\epsilon_k = \mathcal{N}(\epsilon_k | 0,\sigma^2)$ with known $\sigma^2=1$. We are interested in deriving an estimator for $A$.
(a) Make a reasonable assumption for a prior on $A$ and derive a Bayesian (posterior) estimate.
(b) Derive the Maximum Likelihood estimate for $A$.
(c) Derive the MAP estimates for $A$.
(d) Now assume that we do not know the variance of the noise term? Describe the procedure for Bayesian estimation of both $A$ and $\sigma^2$ (No need to fully work out to closed-form estimates).
[5] (##) We consider the coin toss example from the notebook and use a conjugate prior for a Bernoulli likelihood function.
(a) Derive the Maximum Likelihood estimate.
(b) Derive the MAP estimate.
(c) Do these two estimates ever coincide (if so under what circumstances)?[6] (###) Given a single observation $x_0$ from a uniform distribution $\mathrm{Unif}[0,1/\theta]$, where $\theta > 0$.
(a) Show that $\mathbb{E}[g(x_0)] = \theta$ if and only if $\int_0^{1/\theta} g(u) du =1$.
(b) Show that there is no function $g$ that satisfies the condition for all $\theta > 0$.
Continuous Data and the Gaussian Distribution¶
- [1] (##) We are given an IID data set $D = \{x_1,x_2,\ldots,x_N\}$, where $x_n \in \mathbb{R}^M$. Let's assume that the data were drawn from a multivariate Gaussian (MVG),
(a) Derive the log-likelihood of the parameters for these data.
(b) Derive the maximum likelihood estimates for the mean $\mu$ and variance $\Sigma$ by setting the derivative of the log-likelihood to zero.
[2] (#) Shortly explain why the Gaussian distribution is often preferred over other distributions with the same support?
[3] (###) Proof that the Gaussian distribution is the maximum entropy distribution over the reals with specified mean and variance.
[4] (##) Proof that a linear transformation $z=Ax+b$ of a Gaussian variable $\mathcal{N}(x|\mu,\Sigma)$ is Gaussian distributed as
- [5] (#) Given independent variables
$x \sim \mathcal{N}(\mu_x,\sigma_x^2)$ and $y \sim \mathcal{N}(\mu_y,\sigma_y^2)$, what is the PDF for $z = A\cdot(x -y) + b$?
- [6] (##) Compute
Discrete Data and the Multinomial Distribution¶
- [1] (##) We consider IID data $D = \{x_1,x_2,\ldots,x_N\}$ obtained from tossing a $K$-sided die. We use a binary selection variable
with probabilities $p(x_{nk} = 1)=\theta_k$.
(a) Write down the probability for the $n$th observation $p(x_n|\theta)$ and derive the log-likelihood $\log p(D|\theta)$.
(b) Derive the maximum likelihood estimate for $\theta$.
- [2] (#) In the notebook, Laplace's generalized rule of succession (the probability that we throw the $k$th face at the next toss) was derived as
Provide an interpretation of the variables $m_k,N,\alpha_k,\sum_k$ and $\alpha_k$.
[3] (##) Show that Laplace's generalized rule of succession can be worked out to a prediction that is composed of a prior prediction and data-based correction term.
[4] (#) Verify that
(a) the categorial distribution is a special case of the multinomial for $N=1$.
(b) the Bernoulli is a special case of the categorial distribution for $K=2$.
(c) the binomial is a special case of the multinomial for $K=2$.[5] (###) Determine the mean, variance and mode of a Beta distribution.
[6] (###) Consider a data set of binary variables $D=\{x_1,x_2,\ldots,x_N\}$ with a Bernoulli distribution $\mathrm{Ber}(x_k|\mu)$ as data generating distribution and a Beta prior for $\mu$. Assume that you make $n$ observations with $x=1$ and $N-n$ observations with $x=0$. Now consider a new draw $x_\bullet$. We are interested in computing $p(x_\bullet|D)$. Show that the mean value for $p(x_\bullet|D)$ lies in between the prior mean and Maximum Likelihood estimate.
Regression¶
[1] (#) (a) Write down the generative model for Bayesian linear ordinary regression (i.e., write the likelihood and prior).
(b) State the inference task for the weight parameter in the model.
(c) Why do we call this problem linear?[2] (##) Consider a linear regression problem
with $y, X$ and $w$ as defined in the notebook.
(a) Work out the maximum likelihood solution for linear regression by solving
$$
\nabla_{w} \log p(y|X,w) = 0 \,.
$$
(b) Work out the MAP solution. How does it relate to the ML solution?
[3] (###) Show that the variance of the predictive distribution for linear regression decreases as more data becomes available.
[4] (#) Assume a given data set $D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_N,y_N)\}$ with $x \in \mathbb{R}^M$ and $y \in \mathbb{R}$. We propose a model given by the following data generating distribution and weight prior functions:
(a) Write down Bayes rule for generating the posterior $p(w|D)$ from a prior and likelihood.
(b) Work out how to compute a distribution for the predicted value $y_\bullet$, given a new input $x_\bullet$.
- [5] (#) In the class we use the following prior for the weights:
(a) Give some considerations for choosing a Gaussian prior for the weights.
(b) We could have chosen a prior with full (not diagonal) covariance matrix $p(w|\alpha) = \mathcal{N}\left(w | 0, \Sigma \right)$. Would that be better? Give your thoughts on that issue.
(c) Generally we choose $\alpha$ as a small positive number. Give your thoughts on that choice as opposed to choosing a large positive value. How about choosing a negative value for $\alpha$?
Generative Classification¶
- [1] You have a machine that measures property $x$, the "orangeness" of liquids. You wish to discriminate between $C_1 = \text{`Fanta'}$ and $C_2 = \text{`Orangina'}$. It is known that
The prior probabilities $p(C_1) = 0.6$ and $p(C_2) = 0.4$ are also known from experience.
(a) (##) A "Bayes Classifier" is given by
Derive the optimal Bayes classifier.
(b) (###) The probability of making the wrong decision, given $x$, is
$$ p(\text{error}|x)= \begin{cases} p(C_1|x) & \text{if we decide $C_2$} \\ p(C_2|x) & \text{if we decide $C_1$} \end{cases} $$Compute the total error probability $p(\text{error})$ for the Bayes classifier in this example.
[2] (#) (see Bishop exercise 4.8): Using (4.57) and (4.58) (from Bishop's book), derive the result (4.65) for the posterior class probability in the two-class generative model with Gaussian densities, and verify the results (4.66) and (4.67) for the parameters $w$ and $w0$.
[3] (###) (see Bishop exercise 4.9).
[4] (##) (see Bishop exercise 4.10).
Discriminative Classification¶
- [1] Given a data set $D=\{(x_1,y_1),\ldots,(x_N,y_N)\}$, where $x_n \in \mathbb{R}^M$ and $y_n \in \{0,1\}$. The probabilistic classification method known as logistic regression attempts to model these data as
where $\sigma(x) = 1/(1+e^{-x})$ is the logistic function. Let's introduce shorthand notation $\mu_n=\sigma(\theta^T x_n + b)$. So, for every input $x_n$, we have a model output $\mu_n$ and an actual data output $y_n$.
(a) Express $p(y_n|x_n)$ as a Bernoulli distribution in terms of $\mu_n$ and $y_n$.
(b) If furthermore is given that the data set is IID, show that the log-likelihood is given by
$$
L(\theta) \triangleq \log p(D|\theta) = \sum_n \left\{y_n \log \mu_n + (1-y_n)\log(1-\mu_n)\right\}
$$
(c) Prove that the derivative of the logistic function is given by
$$
\sigma^\prime(\xi) = \sigma(\xi)\cdot\left(1-\sigma(\xi)\right)
$$
(d) Show that the derivative of the log-likelihood is
$$
\nabla_\theta L(\theta) = \sum_{n=1}^N \left( y_n - \sigma(\theta^T x_n +b)\right)x_n
$$
(e) Design a gradient-ascent algorithm for maximizing $L(\theta)$ with respect to $\theta$.
[2] Describe shortly the similarities and differences between the discriminative and generative approach to classification.
[3] (Bishop ex.4.7) (#) Show that the logistic sigmoid function $\sigma(a) = \frac{1}{1+\exp(-a)}$ satisfies the property $\sigma(-a) = 1-\sigma(a)$ and that its inverse is given by $\sigma^{-1}(y) = \log\{y/(1-y)\}$.
[4] (Bishop ex.4.16) (###) Consider a binary classification problem in which each observation $x_n$ is known to belong to one of two classes, corresponding to $y_n = 0$ and $y_n = 1$. Suppose that the procedure for collecting training data is imperfect, so that training points are sometimes mislabelled. For every data point $x_n$, instead of having a value $y_n$ for the class label, we have instead a value $\pi_n$ representing the probability that $y_n = 1$. Given a probabilistic model $p(y_n = 1|x_n,\theta)$, write down the log-likelihood function appropriate to such a data set.
[5] (###) Let $X$ be a real valued random variable with probability density
Also $Y$ is a real valued random variable with conditional density
$$
p_{Y|X}(y|x) = \frac{e^{-(y-x)^2/2}}{\sqrt{2\pi}},\quad\text{for all $x$ and $y$}.
$$
(a) Give an (integral) expression for $p_Y(y)$. Do not try to evaluate the integral.
(b) Approximate $p_Y(y)$ using the Laplace approximation.
Give the detailed derivation, not just the answer.
Hint: You may use the following results.
Let
$$g(x) = \frac{e^{-x^2/2}}{\sqrt{2\pi}}$$
and
$$
h(x) = \frac{e^{-(y-x)^2/2}}{\sqrt{2\pi}}$$
for some real value $y$. Then:
$$\begin{align*}
\frac{\partial}{\partial x} g(x) &= -xg(x) \\
\frac{\partial^2}{\partial x^2} g(x) &= (x^2-1)g(x) \\
\frac{\partial}{\partial x} h(x) &= (y-x)h(x) \\
\frac{\partial^2}{\partial x^2} h(x) &= ((y-x)^2-1)h(x)
\end{align*}$$
Latent Variable Models and Variational Bayes¶
- [1] (##) For a Gaussian mixture model, given by generative equations
proof that the marginal distribution for observations $x_n$ evaluates to
$$ p(x) = \sum_{j=1}^K \pi_k \cdot \mathcal{N}\left( x | \mu_j, \Sigma_j \right) $$[2] (#) Given the free energy functional $F[q] = \sum_z q(z) \log \frac{q(z)}{p(x,z)}$, proof the EE, DE and AC decompositions.
[3] (#) The Free energy functional $\mathrm{F}[q] = -\sum_z q(z) \log p(x,z) - \sum_z q(z) \log \frac{1}{q(z)}$ decomposes into "Energy minus Entropy". So apparently the entropy of the posterior $q(z)$ is maximized. This entropy maximization may seem puzzling at first because inference should intuitively lead to more informed posteriors, i.e., posterior distributions whose entropy is smaller than the entropy of the prior. Explain why entropy maximization is still a reasonable objective.
[4] (#) Explain the following update rule for the mean of the Gaussian cluster-conditional data distribution (from the example about mean-field updating of a Gaussian mixture model):
- [5] (##) Consider a model $p(x,z|\theta)$, where $D=\{x_1,x_2,\ldots,x_N\}$ is observed, $z$ are unobserved variables and $\theta$ are parameters. The EM algorithm estimates the parameters by iterating over the following two equations ($i$ is the iteration index):
Proof that this algorithm minimizes the Free Energy functional $$\begin{align*} F[q,\theta] = \sum_z q(z) \log \frac{q(z)}{p(D,z|\theta)} \end{align*}$$
[6] (###) Consult the internet on what overfitting and underfitting is and then explain how FE minimization finds a balance between these two (unwanted) extremes.
[7] (##) Consider a model $p(x,z|\theta) = p(x|z,\theta) p(z|\theta)$ where $x$ and $z$ relate to observed and unobserved variables, respectively. Also available is an observed data set $D=\left\{x_1,x_2,\ldots,x_N\right\}$. One iteration of the EM-algorithm for estimating the parameters $\theta$ is described by ($m$ is the iteration counter)
(a) Apparently, in order to execute EM, we need to work out an expression for the 'responsibility' $p(z|x=D,\hat{\theta}^{(m)})$. Use Bayes rule to show how we can compute the responsibility that allows us to execute an EM step.
(b) Why do we need multiple iterations in the EM algorithm?
(c) Why can't we just use simple maximum log-likelihood to estimate parameters, as described by
$$
\hat{\theta} := \arg \max_\theta \log p(x=D,z|\theta) \,?
$$
Dynamic Models¶
- [1] (##) Given the Markov property
proof that, for any $n$, \begin{align*} p(x_n,x_{n-1},&\ldots,x_{k+1},x_{k-1},\ldots,x_1|x_k) = \\ &p(x_n,x_{n-1},\ldots,x_{k+1}|x_k) \cdot p(x_{k-1},x_{k-2},\ldots,x_1|x_k) \tag{A2}\,. \end{align*} In other words, proof that, if the Markov property A1 holds, then, given the "present" ($x_k$), the "future" $(x_n,x_{n-1},\ldots,x_{k+1})$ is independent of the "past" $(x_{k-1},x_{k-2},\ldots,x_1)$.
[2] (#)
(a) What's the difference between a hidden Markov model and a linear Dynamical system?
(b) For the same number of state variables, which of these two models has a larger memory capacity, and why?[3] (#)
(a) What is the 1st-order Markov assumption?
(b) Derive the joint probability distribution $p(x_{1:T},z_{0:T})$ (where $x_t$ and $z_t$ are observed and latent variables respectively) for the state-space model with transition and observation models $p(z_t|z_{t-1})$ and $p(x_t|z_t)$.
(c) What is a Hidden Markov Model (HMM)?
(d) What is a Linear Dynamical System (LDS)?
(e) What is a Kalman Filter?
(f) How does the Kalman Filter relate to the LDS?
(g) Explain the popularity of Kalman filtering and HMMs?
(h) How relates a HMM to a GMM?
Intelligent Agents and Active Inference¶
[1] (##) I asked you to watch a video segment (https://www.vibby.com/watch?vib=71iPtUJxd) where Karl Friston talks about two main approaches to goal-directed acting by agents: (1) choosing actions that maximize (the expectation of) a value function $V(s)$ of the state ($s$) of the environment; or (2) choosing actions that minimize a functional ($F[q(s)]$) of beliefs ($q(s)$) over environmental states ($s$). Discuss the advantage of the latter appraoch.
[2] (#) The good regulator theorem states that a "successful and efficient" controller of the world must contain a model of the world. But it's hard to imagine how just learning a model of the world leads to goal-directed behavior, like learning how to read or drive a car. Which other ingredient do we need to get learning agents to behave as goal-directed agents?
[3] (##) The figure below reflects the state of a factor graph realization of an active inference agent after having pushed action $a_t$ onto the environment and having received observation $x_t$. In this graph, the variables $x_\bullet$, $u_\bullet$ and $s_\bullet$ correspond to observations, and unobserved control and internal states respectively. Copy the figure onto your sheet and draw a message passing schedule to infer a posterior belief (i.e. after observing $x_t$) over the next control state $u_{t+1}$.
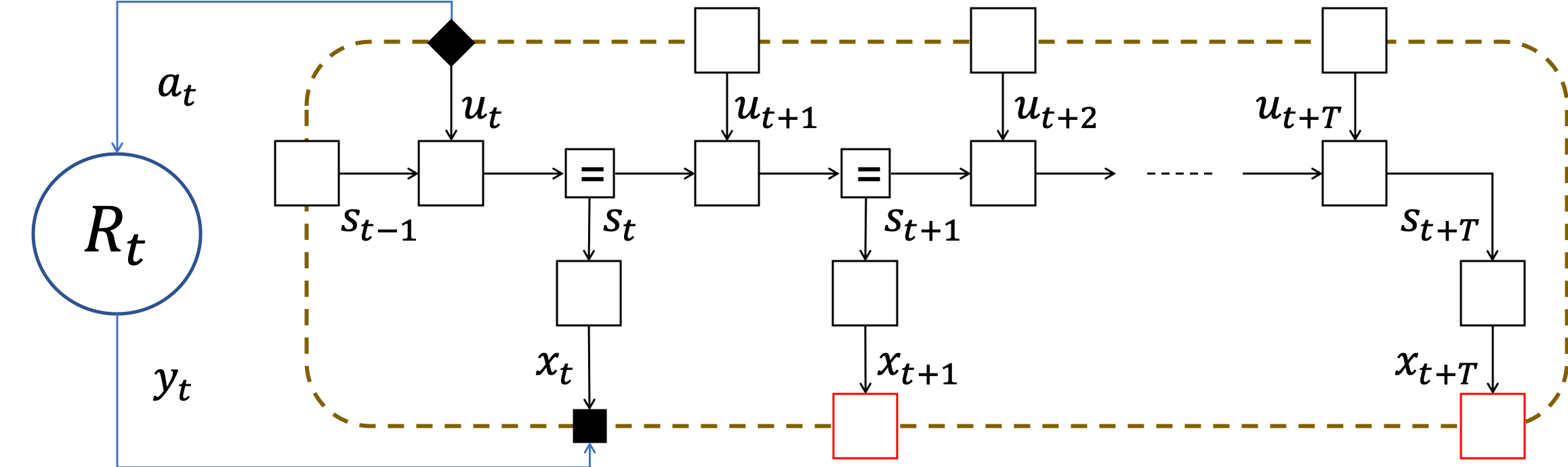
- [4] (##) The Free Energy Principle (FEP) is a theory about biological self-organization, in particular about how brains develop through interactions with their environment. Which of the following statements is not consistent with FEP (and explain your answer):
(a) We act to fullfil our predictions about future sensory inputs.
(b) Perception is inference about the environmental causes of our sensations.
(c) Our actions aim to reduce the complexity of our model of the environment.
open("../../styles/aipstyle.html") do f
display("text/html", read(f,String))
end