Content provided under a Creative Commons Attribution license, CC-BY 4.0; code under BSD 3-Clause license. (c)2014 Lorena A. Barba, Olivier Mesnard. Thanks: NSF for support via CAREER award #1149784.¶
Vortex¶
Let's recap. In the first three lessons of AeroPython, you computed:
a source-sink pair—you learned how to make a
streamplot()and usescatter()to mark the location of the singular points. If you did your challenge task, you saw that equipotential lines are perpendicular to streamlines.a source-sink pair in a free stream, creating a Rankine oval. For the first time, we see that we can model the flow around an object using potential flow solutions. You also learned to define custom functions, to make Python work for you and look even more like plain English.
a doublet—this one is wonderful, because the stream-line pattern gives the flow around a circular cylinder (in two dimensions). You encountered the D'Alembert paradox and hopefully that got you thinking. (If not, go back to that lesson and think!)
Did you also do the assignment? It shows you how a distribution of sources can be used to model potential flow around an airfoil. This starts looking like aerodynamics!
But what is the most important thing we want from applied aerodynamics? We want to make things fly, of course! And to fly, there must be a force of aerodynamic lift to counteract the weight of the object.
In this section of the course, we learn about lift. First, we will compute the flow of a potential vortex. It turns out, vortex circulation and lift are intimately related.
What's a vortex?¶
This question is deeper than you might think! The simple answer is that a vortex is motion in circular streamlines. Imagine streamlines that are concentric circles about a given point—what's confusing is that this does not mean that fluid elements are themselves rotating!
In an irrotational vortex, the tangential velocity is constant along a (circular) streamline and inversely proportional to the radius, while the radial velocity is zero. In polar coordinates:
\begin{equation} u_\theta\left(r,\theta\right) = \frac{\text{constant}}{r} \quad \text{,} \quad u_r\left(r,\theta\right) = 0 \end{equation}The vorticity is zero everywhere, except at the location of the point vortex, where the derivative of $u_\theta$ is infinite.
We introduced the concept of circulation in the first lesson (Source & Sink). Let's use that. Around any circular streamline enclosing the vortex, and using the sign convention that a negative vortex circulates anti-clockwise, we have:
\begin{equation}\Gamma = -\oint \mathbf{v}\cdot d\vec{l} = -u_\theta 2 \pi r\end{equation}Thus, the constant in the expression for $u_\theta$ in $(1)$ is equal to $\Gamma/2\pi$, and we now write:
\begin{equation}u_\theta\left(r,\theta\right) = \frac{\Gamma}{2\pi r}\end{equation}We can get the stream function by integrating the velocity components:
\begin{equation}\psi\left(r,\theta\right) = \frac{\Gamma}{2\pi}\ln r\end{equation}In Cartesian coordinates, the stream function is
\begin{equation}\psi\left(x,y\right) = \frac{\Gamma}{4\pi}\ln\left(x^2+y^2\right)\end{equation}while the velocity components would be:
\begin{equation}u\left(x,y\right) = \frac{\Gamma}{2\pi}\frac{y}{x^2+y^2} \qquad v\left(x,y\right) = -\frac{\Gamma}{2\pi}\frac{x}{x^2+y^2}\end{equation}This vortex flow is irrotational everywhere, except at the vortex center, where it is infinite. The strength of the point vortex is equal to the circulation $\Gamma$ around it.
Let's compute a vortex¶
The set-up is the same as before: we load our favorite libraries, and we create a grid of points to evaluate the velocity field.
import numpy
import math
from matplotlib import pyplot
# embed the figures into the notebook
%matplotlib inline
N = 50 # Number of points in each direction
x_start, x_end = -2.0, 2.0 # x-direction boundaries
y_start, y_end = -1.0, 1.0 # y-direction boundaries
x = numpy.linspace(x_start, x_end, N) # computes a 1D-array for x
y = numpy.linspace(y_start, y_end, N) # computes a 1D-array for y
X, Y = numpy.meshgrid(x, y) # generates a mesh grid
Give your vortex a strength $\Gamma=5$ and place it at the center of your domain:
gamma = 5.0 # strength of the vortex
x_vortex, y_vortex = 0.0, 0.0 # location of the vortex
We will define two functions,
get_velocity_vortex()andget_stream_function_vortex(),
to compute the velocity components and the stream function on our Cartesian grid, given the strength and the location of the vortex. Then, we will use our custom functions to evaluate everything on the grid points. Let's write those functions first.
def get_velocity_vortex(strength, xv, yv, X, Y):
"""
Returns the velocity field generated by a vortex.
Parameters
----------
strength: float
Strength of the vortex.
xv: float
x-coordinate of the vortex.
yv: float
y-coordinate of the vortex.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
u: 2D Numpy array of floats
x-component of the velocity vector field.
v: 2D Numpy array of floats
y-component of the velocity vector field.
"""
u = +strength / (2 * math.pi) * (Y - yv) / ((X - xv)**2 + (Y - yv)**2)
v = -strength / (2 * math.pi) * (X - xv) / ((X - xv)**2 + (Y - yv)**2)
return u, v
def get_stream_function_vortex(strength, xv, yv, X, Y):
"""
Returns the stream-function generated by a vortex.
Parameters
----------
strength: float
Strength of the vortex.
xv: float
x-coordinate of the vortex.
yv: float
y-coordinate of the vortex.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
psi: 2D Numpy array of floats
The stream-function.
"""
psi = strength / (4 * math.pi) * numpy.log((X - xv)**2 + (Y - yv)**2)
return psi
An now, call the functions with the vortex strength and position, plus the coordinates of the evaluation grid, to get the velocity and streamfunction of the vortex.
# compute the velocity field on the mesh grid
u_vortex, v_vortex = get_velocity_vortex(gamma, x_vortex, y_vortex, X, Y)
# compute the stream-function on the mesh grid
psi_vortex = get_stream_function_vortex(gamma, x_vortex, y_vortex, X, Y)
We are now able to visualize the streamlines of a vortex, and they look like concentric circles around the vortex center, as expected.
# plot the streamlines
width = 10
height = (y_end - y_start) / (x_end - x_start) * width
pyplot.figure(figsize=(width, height))
pyplot.xlabel('x', fontsize=16)
pyplot.ylabel('y', fontsize=16)
pyplot.xlim(x_start, x_end)
pyplot.ylim(y_start, y_end)
pyplot.streamplot(X, Y, u_vortex, v_vortex,
density=2, linewidth=1, arrowsize=1, arrowstyle='->')
pyplot.scatter(x_vortex, y_vortex, color='#CD2305', s=80, marker='o');
Vortex & Sink¶
For fun, let's use our superposition powers. Add a vortex to a sink, using two new functions to compute the velocity components and the stream function of the sink, and adding to those of a vortex (remember that the sink can be easily replaced by a source by just changing the sign of the strength).
strength_sink = -1.0 # strength of the sink
x_sink, y_sink = 0.0, 0.0 # location of the sink
def get_velocity_sink(strength, xs, ys, X, Y):
"""
Returns the velocity field generated by a sink.
Parameters
----------
strength: float
Strength of the sink.
xs: float
x-coordinate of the sink.
ys: float
y-coordinate of the sink.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
u: 2D Numpy array of floats
x-component of the velocity vector field.
v: 2D Numpy array of floats
y-component of the velocity vector field.
"""
u = strength / (2 * math.pi) * (X - xs) / ((X - xs)**2 + (Y - ys)**2)
v = strength / (2 * math.pi) * (Y - ys) / ((X - xs)**2 + (Y - ys)**2)
return u, v
def get_stream_function_sink(strength, xs, ys, X, Y):
"""
Returns the stream-function generated by a sink.
Parameters
----------
strength: float
Strength of the sink.
xs: float
x-coordinate of the sink.
ys: float
y-coordinate of the sink.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
psi: 2D Numpy array of floats
The stream-function.
"""
psi = strength / (2 * math.pi) * numpy.arctan2((Y - ys), (X - xs))
return psi
# compute the velocity field on the mesh grid
u_sink, v_sink = get_velocity_sink(strength_sink, x_sink, y_sink, X, Y)
# compute the stream-function on the mesh grid
psi_sink = get_stream_function_sink(strength_sink, x_sink, y_sink, X, Y)
Now, let's visualize the streamlines of the vortex-sink, and admire our artistic creation:
# superposition of the sink and the vortex
u = u_vortex + u_sink
v = v_vortex + v_sink
psi = psi_vortex + psi_sink
# plot the streamlines
width = 10
height = (y_end - y_start) / (x_end - x_start) * width
pyplot.figure(figsize=(width, height))
pyplot.xlabel('x', fontsize=16)
pyplot.ylabel('y', fontsize=16)
pyplot.xlim(x_start, x_end)
pyplot.ylim(y_start, y_end)
pyplot.streamplot(X, Y, u, v, density=2, linewidth=1, arrowsize=1, arrowstyle='->')
pyplot.scatter(x_vortex, y_vortex, color='#CD2305', s=80, marker='o');
Very cool op-art. (And a good model for your typical bath-tub vortex.) But is all this useful? Yes!
First, you will take your training wheels off and—on your own—compute the flow of an infinite row of vortices. Your mission, should you choose to accept it, is in the next notebook.
After that, we will learn about the connection between a vortex, and the force of lift. This turns out to be very important in aerodynamics!
What's this "irrotational" vortex thing?¶
I know what you are thinking.
What does it mean that the vortex is irrotational? Surely if there's a vortex, there's rotation!
You are not crazy. It's natural to think this way, but the potential vortex is a flow where streamlines are circular, yet fluid elements do not rotate around themselves—they just go around the circular path.
This classic video will help you understand ... just watch the 25 seconds of video after time 4m 25s, and see a "vorticity meter" go around a free vortex without rotating itself.
from IPython.display import YouTubeVideo
from datetime import timedelta
start=int(timedelta(hours=0, minutes=4, seconds=25).total_seconds())
YouTubeVideo("loCLkcYEWD4", start=start)
Remember: vorticity measures the local angular velocity of each fluid element. If the fluid elements go around a circular path, but do not spin themselves, there is no vorticity!
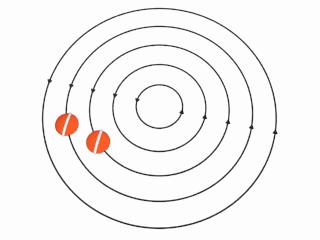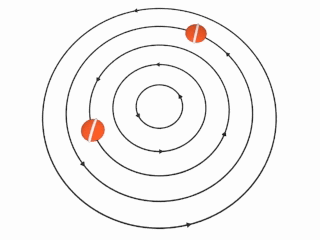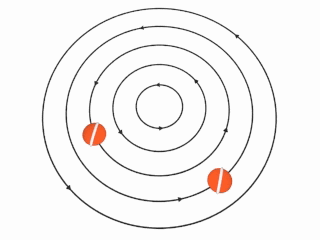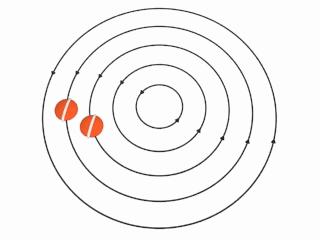
This animation from Wikipedia helps further illustrate what happens in an irrotational vortex: the orange markers with a line across them are going around in circles, but they are not themselves rotating (notice the white lines keep their orientation).
Next ...¶
The next IPython Notebook of the AeroPython series presents the exercise "Infinite row of vortices," as independent student work.
from IPython.core.display import HTML
def css_styling(filepath):
styles = open(filepath, 'r').read()
return HTML(styles)
css_styling('../styles/custom.css')